具有比例依赖的非自治捕食者-两互惠食饵系统的动力学行为

艾合麦提·麦麦提阿吉

(新疆大学数学与系统科学学院，新疆 乌鲁木齐830046)

1.引言

在现实世界中，两个种群之间的相互作用有多种类型，其中捕食-食饵关系是最常见的生态相互作用之一.众所周知，近年来国内外诸多学者对种群捕食者-食饵动力系统进行了广泛的研究，并且研究工作取得了很大的进展.[1-5]到目前为止，在种群捕食者-食饵动力系统研究方面已经建立了许多重要且有意义的结果.其基本和重要的研究问题主要是包括种群的持久性和灭绝性系统正周期解的存在性，全局稳定性和全局吸引性等等.值得注意的是，大多数捕食者-食饵动力系统研究中在描述捕食者及其食饵的动态相互作用时，总是利用比例依赖函数(功能反应函数)来描述捕食者的捕食率和转化率.然而，最近有些种群动力学模型方面的研究利用比例依赖函数来描述种群之间的竞争关系和互惠关系(合作关系)并建立动力学模型[6-13].例如，在文[7]中May首先提出了以下具有比例依赖的两种群合作系统

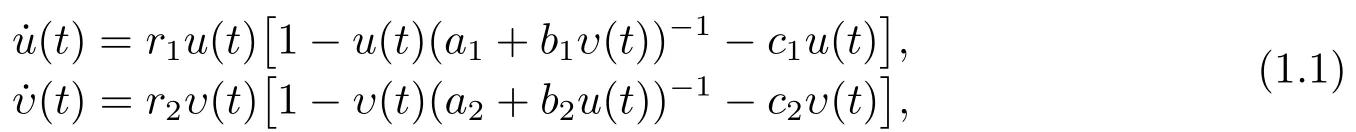
其中u(t)和v(t)表示两个合作种群u和υ在时刻t的密度;u(t)(a1+b1υ(t))-1和υ(t)(a2+b2u(t))-1描述种群u和种群υ 之间合作关系.后来这种具有比例依赖的合作系统被称为May型合作系统[9].文[9-10]在文[7]研究模型的基础上进一步研究了具有时滞的多种群May型合作系统和具有时滞和扩散的两种群May型合作系统的动力学行为.另外，最近文[11]研究了以下捕食者-食饵-合作系统

的持久性.其中x(t)和y(t)表示两个合作食饵种群x和y在时刻t的密度; z(t)表示捕食者种群z在时刻t的密度.在系统(1.2)中作者用来同时描述了捕食者和两个食饵之间的捕食-食饵-合作关系.在本文中结合以上的研究工作和模型，考虑下面的具有比例依赖的非自治捕食者-两互惠食饵系统:

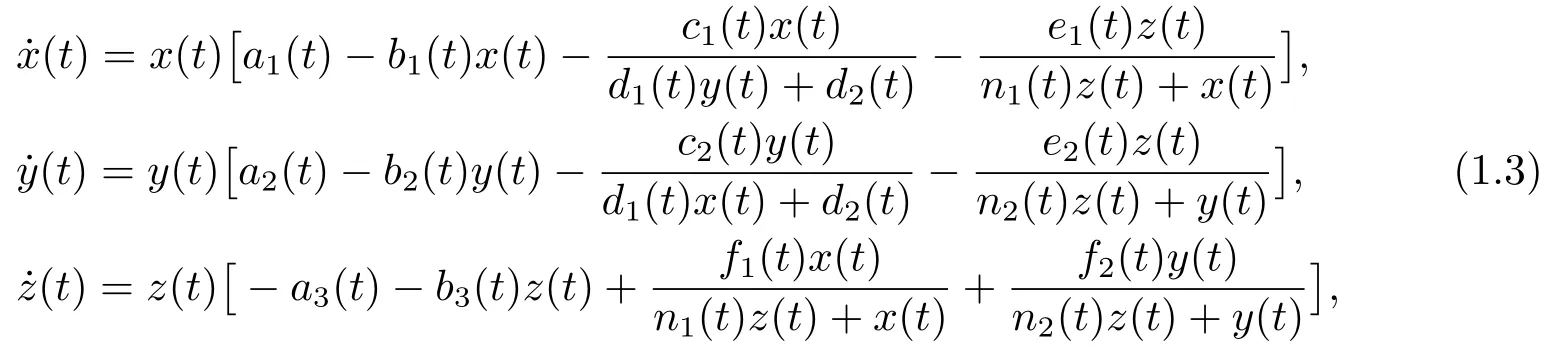
其中x(t)，y(t)分别表示两互惠食饵种群x和y在时刻t的密度;z(t)表示捕食者种群z在时刻t的密度; ai(t)(i = 1，2，3)是种群x，y和z在时刻t的增长率; bi(t)(i = 1，2，3)分别表示种群x，y和z在时刻t内部密度制约项.在系统(1.3)中考虑了一个捕食者和两个食饵，并且用和来描述了两个食饵之间的互惠关系，用来描述捕食者和食饵之间的捕食-食饵关系.系统(1.3)迄今未曾被研究过，并且目前已研究过的大部分其他比例依赖的捕食者-食饵-合作系统主要研究了模型的持久性，灭绝性和正周期解的存在性，几乎没有研究过系统的全局吸引性.因此，本文章将研究系统(1.3)的有界性，持久性，灭绝性，正周期解的存在性以及全局吸引性等动力学行为.

2.预备知识

由系统(1.3)的实际生物意义，我们假设系统(1.3)满足下面的初始条件:

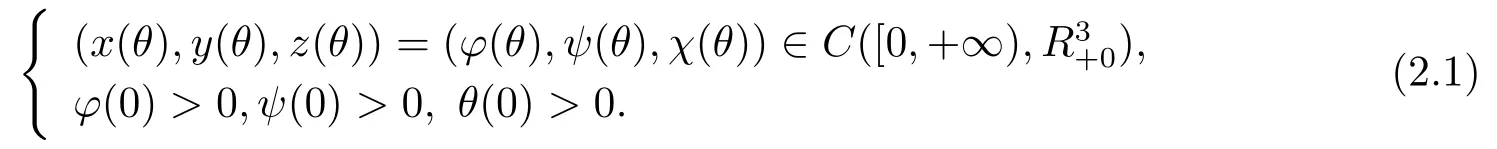
(H1) ai(t)，bi(t)(i=1，2，3)，ci(t)，di(t)，ei(t)(i=1，2)和fi(t)(i=1，2)是在区间[0，+∞)上有界，连续的正函数.

为了叙述方便，对任意在区间[0，+∞)上连续的函数f(t)，我们用下面的记号

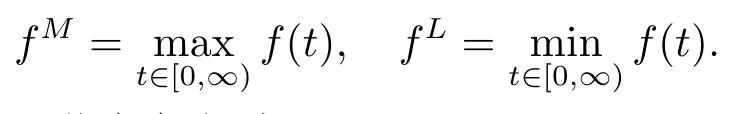
此外，我们还将用到如下一些定义和引理

定义2.1[3]我们称系统(1.3)是持久的，如果存在正的常数mi，Mi(i = 1，2，3)和T*使得系统(1.3) 的每个正解(x(t)，y(t)，z(t))对于任何给定初始条件Φ满足m1≤x(t) ≤M1，m2≤y(t)≤M2，m3≤z(t)≤M3，∀t ≥T*，其中T*依赖于Φ.

定义2.2[12]称系统(1.3)是全局吸引的如果系统(1.3)的任意的两个解(x(t)，y(t)，z(t))和(u(t)，v(t)，µ(t)) 满足

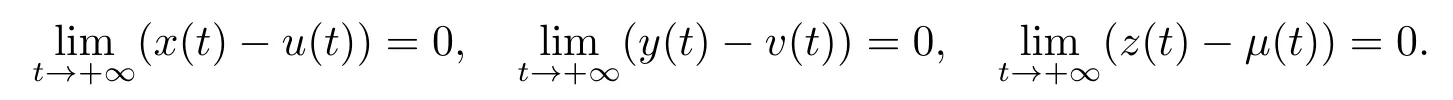
引理2.1[12]考虑下面的方程

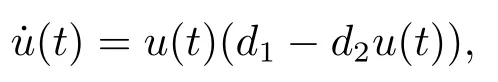
其中d2＞0，我们有下面的结论:

1) 如果d1＞0，那么

2) 如果d1＜0，那么=0.

引理2.2[13]若存在正常数m和M 使得对任何中任Φ ∈[-τ，0]，都有

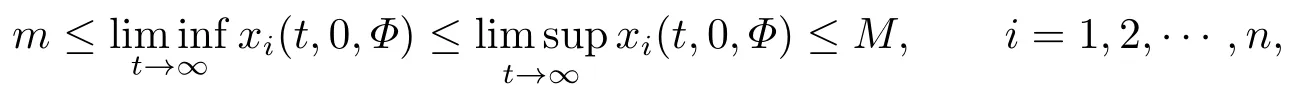
则下面一般形式的泛函微分方程

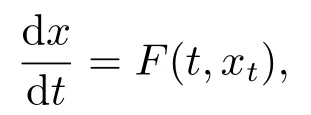
一定存在周期为ω的正周期解，其中x(t) ∈ Rn而F(t，xt)是n维连续实泛函，x(t，0，Φ) =(x1(t，0，Φ)，x2(t，0，Φ)，··· ，xn(t，0，Φ)).

引理2.3[14]设f是定义在[0，∞)上的一个非负函数使得在[0，∞)上可积并且在[0，∞)上一致连续，则

3.系统的有界性，持久性以及正周期解的存在性

定理3.1假设(H1)成立，则系统(1.3)是最终有界的.

证首先，由系统(1.3)的第一个方程对t ≥0我们可以得到，

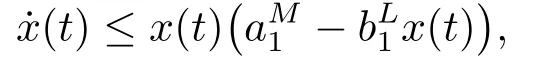
考虑下面的辅助方程

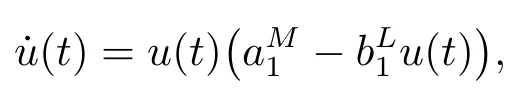
由引理2.1，可以得到

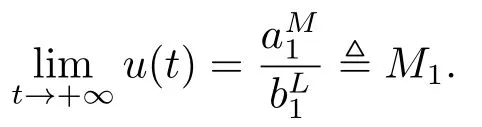
根据微分方程的比较原理，存在一个常数T0＞0使得x(t) ≤M1，其中t ≥T0.其次，由系统(1.3)的第二个和第三个方程对t ≥0可以得到，

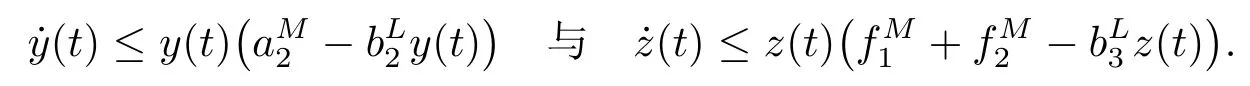
然后，类似于上面的讨论，存在一个常数T1＞0使得对t ≥T1有y(t)≤M2和z(t)≤M3，其中

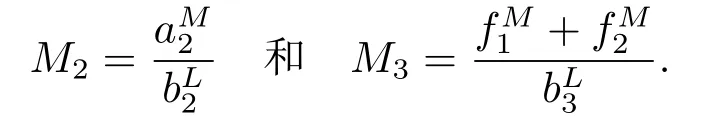
定理3.2假设(H1)成立并且Ai＞0(i = 1，2)，则存在常数m1＞0，m2＞0，使得系统(1.3)的任一个正解(x(t)，y(t)，z(t))满足下面的条件

证由系统(1.3)的第二个和第三个方程对t ≥0可以得到，

定理3.3假设系统(1.3)满足定理3.2的全部条件并且满足A3＞0，则系统(1.3)是持久的，其中

证由定理3.1和定理3.2，存在常数T4＞0，使得对任意给定的常数ε0＞0有

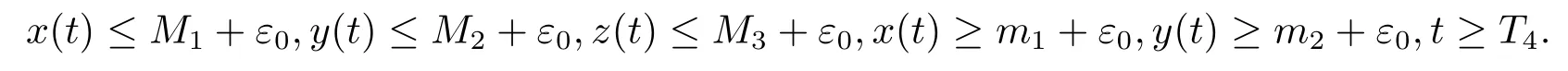
由系统(1.3)的第三个方程得到

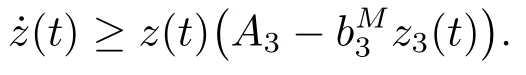
由ε0的任意性且类似于定理3.2中的讨论，存在常数T5＞0，使得对t ≥T5有z(t) ≥m3，其中

故，根据定义2.1，系统(1.3)是持久的.

由引理2.1 可以得到下面的推论.

推论3.1假设(H1)成立并且A4＜0，则捕食者种群z灭绝，其中

下面假设系统(1.3)为周期系统的条件下得到系统至少存在一个正周期解的充分条件.

(H2) ai(t)，bi(t)(i=1，2，3)，ci(t)，di(t)，ei(t)(i=1，2)和fi(t)(i=1，2)都是ω-周期非负连续函数.

由引理2.2可以得到下面的推论.

推论3.2假设(H2)成立并且Ai＞0(1，2，3)，则系统(1.3)至少有一个正ω-周期解.

4.系统的全局吸引性

首先，为了方便我们介绍一些记号

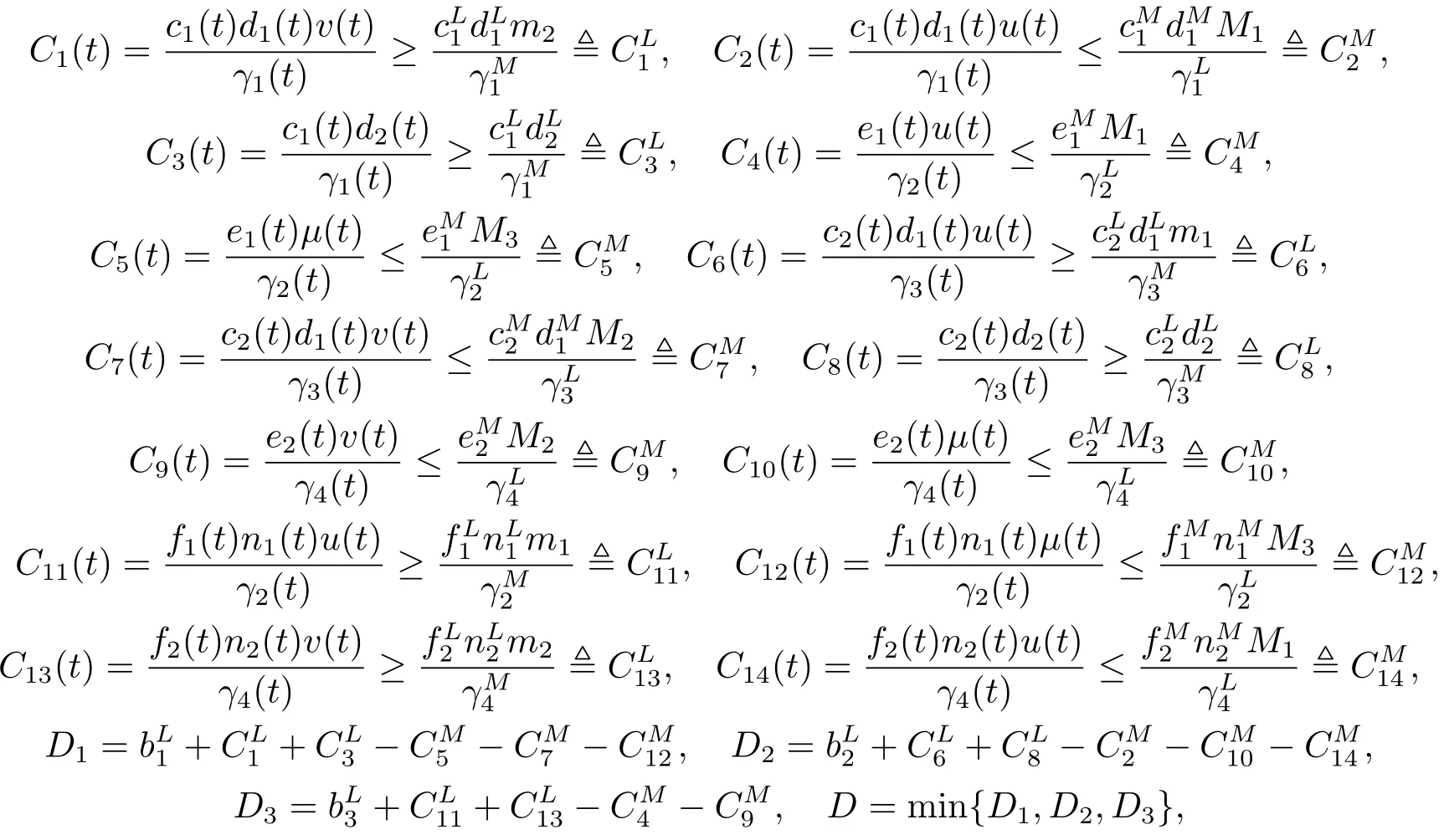
其中

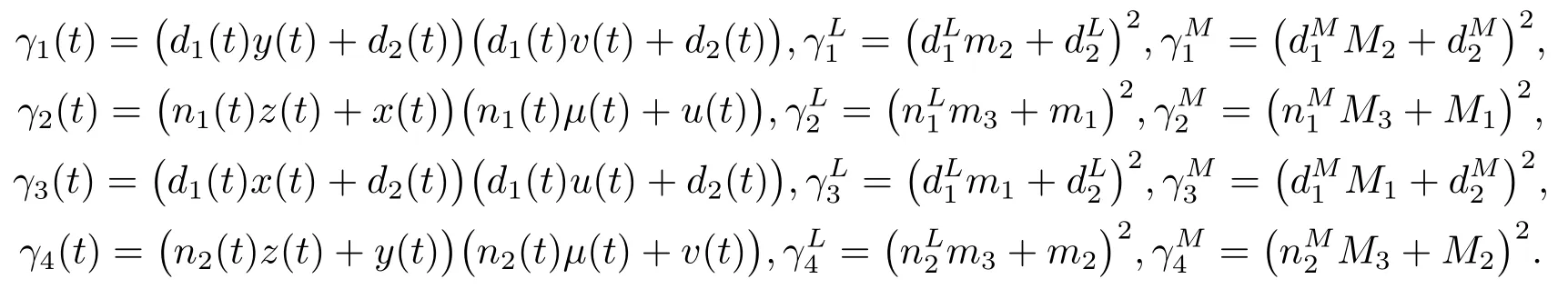
关于系统(1.3)的全局吸引性，我们有下面的结论.

定理4.1假设系统(1.3)满足定理3.3的全部条件并且满足D ＞0，则对系统(1.3)是全局吸引的.

证设(x(t)，y(t)，z(t))和(u(t)，v(t)，µ(t))是系统(1.3)的任意两个正解.由系统(1.3)的持久性，存在常数T ＞0，mi＞0，Mi＞0(i = 1，2，3)使得m1≤x(t) ≤M1，m2≤y(t) ≤M2，m3≤z(t)≤M3对一切t ≥T成立.定义Liapunov函数

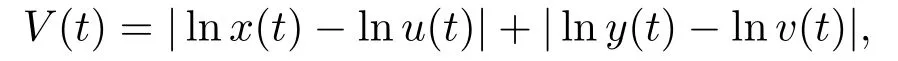
则沿着系统(1.3)计算V(t)的右上导数，得到

在区间[T，t]上积分(4.1)，我们得到

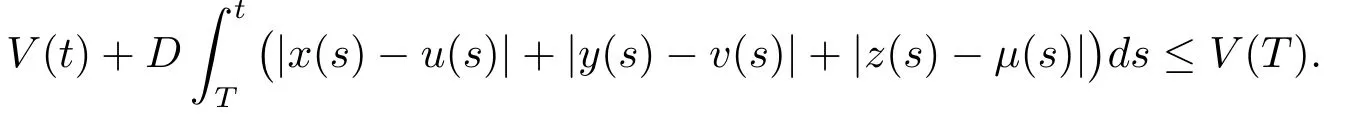
因此，V(t)在区间[T，∞)上有界，从而得到

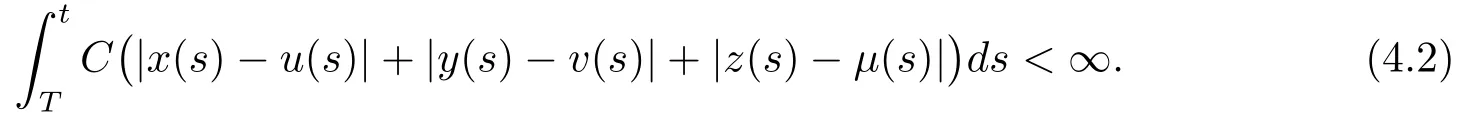
由系统(1.3)的持久性和(4.2)我们可以得到|x(s)-u(s)|+|y(s)-v(s)|+|z(s)-µ(s)|和它们的导数在区间[T，+∞)上有界的.从而由引理2.3(Barbalat引理)得到

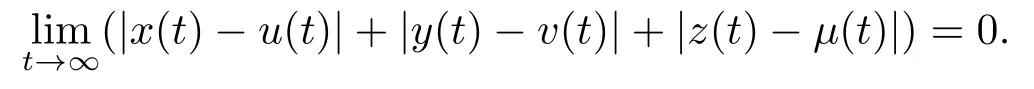
因此，

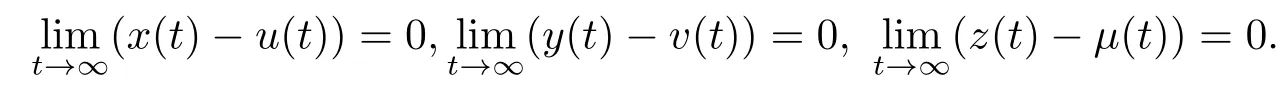
由定理4.1和推论3.2，有下面的结论

推论4.1假设条件(H2)成立，且Di＞0(i = 1，2，3)，则系统(1.3)有一个全局吸引的正ω-周期解.