时延与丢包情形下的网络控制系统量化反馈镇定
王春平
(浙江理工大学 科技与艺术学院,浙江 上虞 312369)
0 引言
网络控制系统(NCSs,networked control systems)是通过一个实时网络来形成闭环的反馈控制系统,它由控制器、多个执行器、被控对象、多个传感器和控制网络构成的[1-2]。由于通信网络的介入,闭环反馈回路(即传感器-控制器通道和控制器-执行器通道)中的各种数据传递都要通过这个控制网络才能实现。相较于传统的简单控制系统,NCSs可以减少系统布线,能够实现对系统的实时监测与控制,易于对系统进行诊断和维护;还能通过网络实现信息共享,增加系统的灵活性,还有其他许多优点。基于这些优势,NCSs已经在航空航天系统、电力系统、工业过程控制系统、汽车控制系统等领域受到了广泛的关注与应用。
但同时,也正是因为在反馈回路中引入了通信网络,很多在传统控制理论中的很多理想性假设需要被重新考虑。比如传统控制理论中系统组件之间是点对点的,传感器-控制器通道和控制器-执行器通道之间信息传递不存在时延,而且在网络环境中,多个节点共用一个通信网络,可能会导致网络阻塞甚至中断,由此会引发网络诱导时延与数据包丢失或乱序。由此导致控制系统的分析与设计变得更加复杂。NCSs涉及的通信数据都是数字信号的,即连续信号在被传输之前必须经过数据量化的处理[3-4],这会影响控制器接收传感器发送的采样数据以及执行器接收控制器发出的控制数据,严重时会导致系统失稳。所以控制系统的分析与设计变得尤为关键。
基于此,本文针对短时延NCSs,考虑两个通道(传感器-控制器通道和控制器-执行器通道)都存在数据包丢失以及传感器-控制器通道设置量化器存时的系统稳定性问题,对系统进行了建模、稳定性分析与控制器设计,并利用Matlab的线性矩阵不等式即LMI(linear matrix inequality)工具箱[5]进行了算例仿真验证。
1 网络控制系统结构与建模
假设丢包概率一定,那么丢包过程可以等效为按一定速率切换的开关,开关闭合表示数据正常传输,开关打开表示发生数据丢包[6-8]。另外,NCSs中最常见的另外一个现象就是网络诱导时延,如果系统设计没有考虑网络诱导时延的影响,那么控制系统的性能可能会得到降低,严重时甚至使得系统失稳。因此,本文进一步考虑系统存在短时延的情况,如果将传感器-控制器通道存在的时延记为τsc,控制器-执行器通道存在的时延,记为τca,那么网络总时延τ=τsc+τca 图1 存在短时延和丢包的NCSs模型 由于网络通讯带宽受限,为保证采集的数据信号传输质量,在保证系统性能的前提下尽可能降低通信资源占用率,我们在网络传输通道中引入对数量化器,记为h(x)。通过量化器,我们可以将传感器采集到的连续信号进行量化处理,转化为一定数量的离散信号,这些离散信号可以代表传感器采集的信号,编码、传输这些离散信号可以在极大程度上降低连续信号的传输量。 量化器记为h(x)=[h1(x1)h2(x2)hn(xn)],定义如下: 记Δh=diag{Δh1,Δh2,,Δhn},其中,Δhm∈[-εhm,εhm]。根据文献[3],有: h(x)=(I+Δh)x 假设系统采用输入零阶保持器策略,即在数据包到达之前保持前一周期的输入,且传感器采用时间驱动,控制器和执行器采用事件驱动。那么,我们可以将系统描述为以下4种情况: 1)开关S1,S2都闭合: 2)开关S1闭合,开关S2打开: up(k)=up(k-1) 3)开关S1打开,开关S2闭合: xc(k)=xc(k-1) up(k)=up(k-1) 4)开关S1,S2打开: xc(k)=xc(k-1) up(k)=up(k-1) 进一步将上述结果简化为两种情况:没有发生丢包(开关S1,S2都闭合)与发生丢包(开关S1和S2中至少有一个打开)。如果引入一个二值变量i来表示系统的丢包情况: 那么,当i=1时, 当i=2时, up(k)=up(k-1) 我们可以将图1等效为如图2所示的单边丢包与短时延系统。 图2 等效的单边丢包与短时延NCSs模型 在NCSs中,被控对象一般是连续的,而控制器却是离散的,所以要对其进行离散化。假设连续时间下的被控对象状态模型为: 离散时间下的状态反馈控制器为: uc(k)=K(I+Δh)xc(k)=(K+ΔK)x(k) (1) 令ΔK=K*Δh,那么,离散时间下的被控对象状态模型为[8]: y(k)=Cx(k) (2) x(k+1)= (3) φ(k+1)=Φiφ(k) (4) 其中, 本文考虑的NCSs是同时包含连续时间的被控对象与离散事件的闭环系统,称为异步动态系统(ADS, asynchronous dynamic system),是兼具离散动态和连续动态的系统,也称为混杂系统,由Hassibi等人在1999年首次提出[6],其时间动力学模型由差分方程描述,切换开关描述离散事件动力学模型。数据包到达亦或丢失以及有限开关的开启与闭合均能使用异步动态系统模型。如传感器输出的采样值通过量化器到达控制器,采样数据和反馈数据均通过网络传输,网络的不确定性包括超时等待或拥堵均能导致数据包丢失。文献[7]给出了异步动态系统指数稳定性的条件,本节在此基础上展开NCSs稳定性分析,首先需要用到如下引理。 β1‖x‖2≤V(x)≤β2‖x‖2 其中:β1,2>0;且且存在标量α1,α2,,αN,满足: (5) 则该系统是指数稳定的。 定理3:对式(4)描述的异步动态系统φ(k+1)=Φiφ(k),存在事件Es(i) ={E1,E2},对应事件率为ri={r1,r2},r1+r2=1,选取Lyapunov函数V(φ(k))=φT(k)Pφ(k),P为一个对称正定矩阵。那么,如果存在标量α1,α2,满足: (7) 且存在X=P-1,满足: (8) 则式(4)所描述的NCSs是指数稳定的。 根据引理1中的式(5)可以得到: 即: 将V(φ(k))=φT(k)Pφ(k)代入可得: φT(k+1)Pφ(k+1)-αi(-2)φT(k)Pφ(k)≤0 将: φ(k+1)=Φiφ(k) 代入得: 化简可得: 由于P是一个对称正定矩阵,所以P-1也是对称正定矩阵,将上式分别左乘、右乘P-1,可以得到: 利用引理2可以得到: 设X=P-1,代入上式,得到: 定理3证毕。 仿真算例: 考虑被控对象状态方程描述的NCSs参数如下: (9) 采样周期为0.3 s,控制器和执行器节点都采用事件驱动,系统总网络诱导时延为0.1 s。若控制器增益为K=[-3.50 -11.55],如果系统不发生丢包时是指数稳定的。那么要考虑:当通信网络介入后,发生数据丢包,数据包的传输成功率为r1=0.90,即数据丢包发生的概率为r2=1-r1=0.10,此时,利用Matlab的LMI工具箱构造线性矩阵不等式,求解正定矩阵X,最终可以得到如下结果: 代入到Φ1、Φ2中可得: 通过该例可以验证定理3的结果是有效的,系统指数稳定性可行。 在实际的应用场合中,往往需要通过考虑闭环系统稳定性进而设计控制器参数,本节假设已知NCSs的丢包率,利用LMI工具箱设计控制器参数使闭环NCSs是指数稳定的。 将离散状态空间模型化简为: x(k+1)= i=1,不发生丢包,i=2,发生丢包。 则: (10) 为具有两个离散事件的异步动态系统,要想该系统能够指数稳定,那么需要引理1的两个条件,从而得到满足条件的状态反馈控制器的设计。式(6)可以直接获得,式(5)可以通过线性矩阵不等式[8]得到。 选取李雅普诺夫函数V(x(k))=xT(k)Px(k)+xT(k-1)Qx(k-1),P和Q均为对称的正定矩阵,那么根据引理1中的式(5): 可以得到: 将李雅普诺夫函数代入得: xT(k+1)Px(k+1)+xT(k)Qx(k)- 根据式(10)可以得到: 1)当i=1时: 这里, (11) *表示矩阵相应元素的对称项。 2)当i=2时: (12) 令X=P-1,T=P-1QP-1,Y=KX=KP-1,ΔY=(ΔK)X将式(11)和式(12)化简,最后可以得到如下线性矩阵不等式组: (13) 对式中存在的非线性项进行处理并根据Schur引理,式(13)可等价于: 利用LMI工具箱构造此线性矩阵不等式组,可以求得X、T、Y,控制器参数可以通过K=YX-1获得。 仍然考虑被控对象状态方程如式(9)所示的NCSs: 传感器采样周期0.3 s,系统总网络诱导时延为0.1s,数据包的传输成功率为r1=0.90,即数据丢包发生的概率为r2=1-r1=0.10。 根据引理1的式(6),取α1=1.07,α2=0.6时,则衰减率α=1.034 0>1,满足条件。选择ε=0.02,σ=50。再利用LMI工具箱求解如式(13)的线性矩阵不等式组,可得: 图3 系统存在时延和丢包时的状态响应曲线图 NCSs是控制领域的研究热点,但是由于网络的介入会带来许多问题,应用在分布式控制与存在丢包的情形时[9-12],系统的分析与设计显得尤为重要。本文对存在短时延的NCSs,不仅设置了对数量化器,而且考虑双通道的数据丢包问题,即传感器-控制器通道和控制器-执行器通道同时存在数据包丢失的情况,把系统建模成为具有两个离散事件的异步动态系统。在此基础上,根据异步动态系统稳定性理论进行该NCSs的指数稳定性分析,并利用MATLAB软件的LMI工具箱设计出了该异步动态系统控制器参数,同时进行实验仿真,仿真结果验证了本文方法是有效且可行的。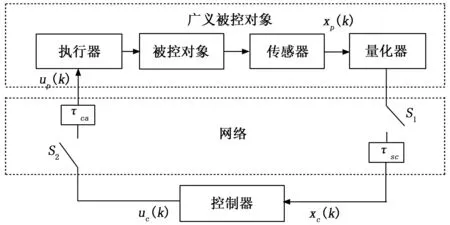
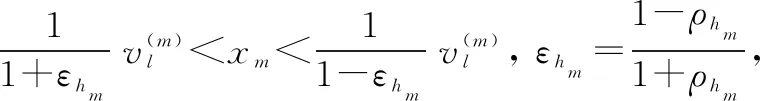




2 指数稳定性分析
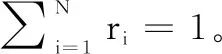





3 状态反馈控制器设计
3.1 LMI处理方法

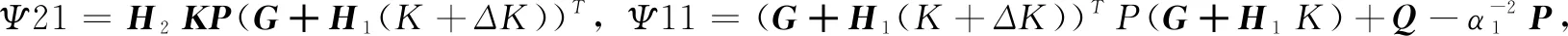
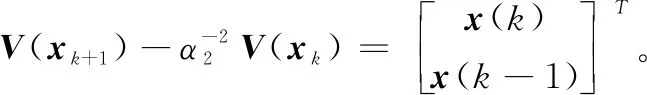
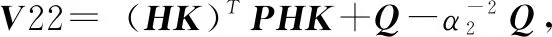
3.2 仿真实验与分析
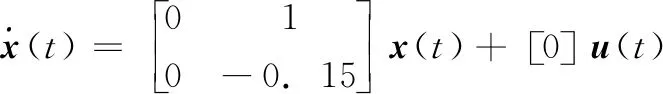
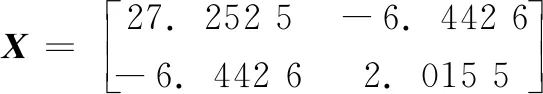



4 结束语

