滚仰式半捷联光电稳定平台误差分析与补偿
赵毅鑫 崔颢 陈晓曾 丁海山






摘 要:為了提高滚仰式半捷联光电稳定平台的视线指向测量精度, 提出一种稳定平台误差建模与参数标定的方法。 针对滚仰式导引头的结构特点, 分析了稳定平台的主要误差来源, 利用坐标变换法和泰勒公式建立了失调角的线性误差模型, 设计了通过补偿失调角误差提高稳定平台的视线指向测量精度方法。 针对稳定平台误差参数标定问题, 利用最小二乘法设计了误差参数标定方法。 仿真结果表明: 误差参数标定方法可以有效标定误差参数, 通过失调角线性误差模型补偿失调角误差的方法可以显著提高稳定平台视线指向测量精度。
关键词: 稳定平台; 装调误差; 参数标定; 补偿; 滚仰式导引头; 最小二乘法; 制导与控制
中图分类号: TJ765.3+31; V248.1文献标识码: A文章编号: 1673-5048(2021)06-0053-05
0 引 言
在现代战争中, 夺取制空权成为决定胜负的关键因素[1]。 红外制导空空导弹是空中对抗的主战武器之一, 小型化是其未来的发展需求[2-3]。 红外导引系统是红外制导空空导弹的重要子系统, 一般由跟踪稳定平台系统、 红外探测系统、 目标信号处理系统和导引信号形成系统组成, 其主要功能是目标寻的和稳定跟踪。 滚仰式半捷联光电稳定平台相较于传统稳定平台具有体积小、 探测范围大的优点, 是新一代空空导弹导引头平台结构的发展方向[4-5]。 失调角是导引头探测器直接测得的弹目视线相对于探测器的方位角和高低角, 其准确性影响着视线在弹体系下的准确指向[6-7]。 由于机械系统误差和测量系统误差的存在, 使得导引头探测器测得的失调角与理想情况下的失调角存在偏差。 对探测器所得失调角数据进行补偿后, 可以显著提高导引头视线测量精度。
为了对失调角进行补偿, 需要建立失调角的误差模型, 并对其中的误差项进行标定。 误差模型建立前, 需要建立包含误差项的平台机构运动学模型。 主要有以下建模方法: 四元数法、 局部指数积法、 球谐函数法、 基本参数法和坐标变换法[8-12]。 其中, 坐标变换法具有模型完整、 精确度高等特点, 被广泛应用[13-15]。 本文全面分析了影响稳定平台视线测量误差的来源, 建立了失调角的线性误差模型, 并设计了稳定平台误差参数标定方法。 最后通过数值仿真验证了线性误差模型和参数标定方法的正确性和有效性。
1 误差模型
滚仰式半捷联稳定平台的机械结构为滚转-俯仰两轴结构, 其中, 滚转框架作为外框架, 俯仰框架作为内框架, 探测器刚性固连在俯仰框架上, 理想情况下弹体纵轴与滚转框架转轴重合, 滚转框架转轴与俯仰框架转轴正交, 俯仰框架处于零位时, 探测器光轴和滚转框架转轴重合。
1.1 坐标系定义
为了分析滚仰式半捷联稳定平台的运动学关系, 基于右手直角坐标定义了如下坐标系。 为了简化, 分析时将各个坐标系进行平移, 使得各个坐标系的原点重合。
(1) 弹体坐标系(b系)O-XbYbZb: 原点O在导弹质心上; OXb轴和弹体的纵轴重合, 方向指向导弹头部; OYb轴在弹体的纵对称面内, 向上为正。
(2) 外环坐标系(o系)O-XoYoZo: 原点O在滚转轴和俯仰轴交点上; OXo轴和外框架转轴固连, 方向指向导弹头部; OZo轴和内框架转轴重合, 方向向外。
(3) 平台坐标系(p系)O-XpYpZp: 原点O在滚转轴和俯仰轴交点上; OZp轴和内框架转轴固连, 电机指向旋变的方向为正方向; 当内框架处于零位时, OXp轴在内框架转轴和外框架转轴确定的平面内, 方向指向导弹头部。
(4) 探测坐标系(d系)O-XdYdZd: 原点O在探测器平面中心上; OXd轴和探测器平面的中垂线重合并指向前方; OYd轴和探测器面上敏感元的行平行, 方向指向外。
理想情况下, 探测坐标系(d系)与平台坐标系(p系)重合, 弹体坐标系(b系)绕OXb轴旋转γs角与外环坐标系(o系)重合, 外环坐标系(o系)绕OZo轴旋转θs角与平台坐标系(p系)重合。
1.2 误差的描述
稳定平台在实际装配过程中, 存在一些装配调校误差, 使得稳定平台指向精度降低。 在不考虑外框架转轴和内框架转轴异面的情况下, 本文将装调误差分为四类: 外框架安装误差、 内框架安装误差、 探测器安装误差、 零位误差。 误差角度的正负由右手法则确定。
1.2.1 外框架安装误差
在理想状态下, 外框架转轴和弹体纵轴重合。 外框架安装误差可由图1中的Δ1=(α1, β1)表示。 其中, α1为OXb轴与外框架转轴在XbOZb平面上投影的夹角; β1为外框架转轴与XbOZb平面的夹角。
1.2.2 内框架安装误差
在理想状态下, 内框架转轴和弹体纵轴重合。 内框架安装误差可由图2中的Δ2=(α2, β2)表示。 其中, α2为内框架转轴与YpOZp平面的夹角, β2为OZp轴与内框架转轴在YpOZp平面上投影的夹角。
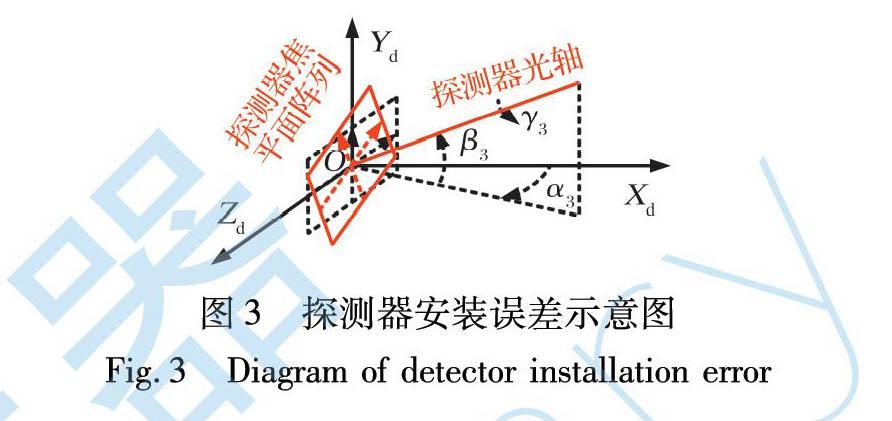
1.2.3 探测器安装误差
在理想状态下, 探测器平面中垂线和OXp轴重合。 探测器安装误差可由图3中的Δ3=(α3, β3, γ3)表示。 显然, 探测系先绕OXd轴转-γ3角, 然后绕OZd轴转-β3角, 最后绕OYd轴转-α3角就和平台坐标系重合。
1.2.4 零位误差
零位误差是由于传感器的零位与设计的框架机械零位不重合导致的, 可分为外框架零位误差δγ和内框架零位误差δθ。
1.3 误差传递建模
由1.2节分析可知, 各坐标系变换之间的误差传递如图4所示。
定义Tx(), Ty(), Tz()分别为坐标系绕相应坐标轴旋转角的坐标变换矩阵。 设弹目视线上的单位矢量r在b系下的投影为Rb。
当不存在装调误差时, 记r在d系下的投影为Rd, 可以得到以下结果:
Rb=Tx(γs)Tz(θs)Rd(1)
当存在装调误差时, 记r在d系下的投影为R′d。 根据图4中坐标系转换关系, 可得以下结果:
Rb=T1R′d(2)
式中:
T1=Ty(α1)Tz(β1)Tx(γs+γ0)Tx(β2)Ty(α2)·
Tz(θs+θ0)Ty(α3)Tz(β3)Tx(γ3)。
由式(1)~(2)联立得到R′d与Rd之间的关系:
Rd=Tz(-θs)Tx(-γs)T1R′d(3)
记理想情况下, 弹目视线在d系下的失调角为(εy, εz)。 其中, εy为方位角, εz为高低角。 则有
Rd=Ty(εy)Tz(εz)100=cosεycosεzsinεz-sinεycosεz(4)
记有误差的真实情况下, b系下的视线矢量R′d对应的失调角为(ε′y, ε′z), 可得
R′d=cosε′ycosε′zsinε′z-sinε′ycosε′z(5)
将式(4)~(5)代入式(3), 可得理想情况下的失调角与有误差情况下的失调角之间的对应关系:
cosεycosεzsinεz-sinεycosεz=Tz(-θs)Tx(-γs)T1cosε′ycosε′zsinε′z-sinε′ycosε′z(6)
1.4 线性误差模型建立
因为误差量和失调角均为小量, 故可以运用泰勒公式将式(6)中包含误差量和失调角的三角函数项展开, 并舍弃高阶小量, 即sinΔ=Δ, cosΔ=1, 可得失调角的线性误差方程为
Δεy=εy-ε′y=bycy
Δεz=εz-ε′z=bzcz (7)
式中:
by=[1 , cosθs , -sinθs, sinγscosθs, cosγscosθs]
bz=[1, cosγs, -sinγs]
cy=[δ2, δ3, δ4, δ5, δ6]T
cz=[δ1, δ5, δ6]T。
其中, cy, cz中各项常量参数与前文分析的误差项之间的对应关系: δ1=β3+δθ, δ2=α3, δ3=α2, δ4=β2+δγ, δ5=β1, δ6=α1。
式(7)中的失调角线性误差主要包含误差项和框架角项。 模型表明: 失调角的误差主要与误差项和框架角有关。
2 标定方法
误差参数标定的目标是基于探测器直接测得的失调角数据标定误差参数的最优值。 一般采用最小二乘法标定其参数。 式(7)每项均为一阶模型, 将其抽象为
f=b1×ncn×1(8)
式中: f为所求问题值; cn×1=[c1, c2, …, cn]T为待定的误差参数; b1×n=[b1, b2, …, bn]为已知变量的函数。 误差参数的辨识过程需要比较失调角的实测值和标定值, 为了更精确地辨识误差参数, 应增加实测工作点。 由仿真试验测得m(m≥n)组数据, 将测量数据按以下向量或矩阵形式表示:
fm×1=[f 1, f 2, …, f m]
Bm×n=[(b11×n)T, (b21×n)T, …, (bm1×n)T]T
假设BTm×n, Bm×n是非奇异的, 运用最小二乘法可得最优参数为
cn×1=(BTm×nBm×n)-1BTm×n fm×1(9)
对式(7)各项分别运用最小二乘法, 即可计算出误差参数标定值:
δ=[δ1, δ2, …, δ6]T
3 数值仿真
为了验证以上模型的正确性和有效性, 设计了以下数值仿真试验。 首先, 随机设计一组误差参数, 将其作为式(2)的参数构建导引头稳定平台模型, 然后由标定方法获得误差参数标定值。 将误差参数标定值代入式(7)中, 获得失调角的线性误差模型。 最后, 在不同框架角条件下, 测试失调角线性误差模型的补偿效果。
3.1 仿真模型建立
设外框架安装误差为Δ1=(-0.205°, 0.295°); 内框架安装误差为Δ2=(-0.23°, 0.3°); 探测器装调误差为Δ3=(-0.25°, 0.12°, -0.5°); 内、 外框架零位誤差分别取为θ0=0.21°, γ0=0.15°。 将以上参数代入式(2)中, 即可构建导引头稳定平台模型。
3.2 误差参数标定仿真
本文通过测量弹体系中单位矢量的失调角, 估算平台误差。 令γs在{-135°, -45°, 45°, 135°}中分别取值, θs在{-45°, 0, 45°}中分别取值, 共形成12组框架角。 设置视线与探测器光轴重合, 即令ε′y=ε′z=0。 将每一组框架角代入构建的导引头稳定平台模型中, 可得真实的弹体系下的视线矢量Rb。 将Rb代入式(1)中, 可得理想情况下的失调角数据, 进而得到该组框架角条件下的失调角误差数据。 将这12组数据代入式(9)中, 即可计算出一组误差参数标定值。 计算结果如下(保留3位有效数字):
δ=[0.327°, -0.250°, -0.233°, 0.448°, 0.295°, -0.205°]
将这组数据代入式(7)中, 构建出失调角的线性误差模型。
3.3 视线指向补偿仿真
由式(7)可知, 失调角误差主要与框架角有关, 失调角本身对于失调角误差的影响很小, 可以忽略, 且在大部分的工作过程中, 导引头光轴可以跟踪上视线。 故在仿真中, 将有误差的真实情况下的失调角项固定, 令视线与探测器光轴重合, 即令ε′y=ε′z=0。 然后, 在不同的框架角条件下, 利用构建的导引头稳定平台模型, 计算出视线上单位向量在弹体系下的真实投影Rb, 即视线的真实指向。 利用式(1)产生导引头实际输出的有误差的弹体系下的视线矢量R′b, 再利用3.2节中构建的失调角的线性误差模型, 计算此框架角条件下的失调角误差(Δεy, Δεz)。 记补偿过后的失调角为ε″y=ε′y+Δεy, ε″z=ε′z+Δεz, 将其代入式(1)中, 产生导引头实际输出补偿后的弹体系下的视线矢量R″b。 记Rb与R′b的夹角为δφ1, Rb与R″b的夹角为δφ2。 δφ1和δφ2分别为补偿前后的视线指向测量误差。
对弹体前半球进行网格数据仿真, 外框架為固定值, 内框架从-60°开始以5°步长运动到60°。 然后, 外框架从-180°开始以5°步长运动到180°重复仿真试验, 形成一个空间网格测试区域。 图5(a)给出了补偿前视线指向测量误差δφ1随框架角的变化图像, 图5(b)给出了补偿后视线指向测量误差δφ2的变化图像。
仿真结果表明: 视线的指向误差主要与空间指向位置有关, 随框架角的变化而变化。 在仿真算例的整个空间网格测试区域内, 失调角线性误差模型均可有效补偿视线的指向误差。 计算可得, 补偿前的视线指向测量误差最大为1.083°, 均值为0.629°, 标准差为0.278°; 补偿后的指向误差最大为0.006°, 均值为0.001°, 标准差为0.000 1°。 补偿后视线指向测量误差的幅值、 均值和标准差均显著减小, 稳定平台的视线指向测量精度显著提高。
4 结 论
本文研究了滚仰式半捷联光电稳定平台误差分析与补偿问题。 建立了失调角的线性误差模型, 利用最小二乘法收敛速度快与误差小的特点, 设计了稳定平台误差参数标定方法。 数值仿真实验结果证明: 视线的指向误差与空间指向位置有关, 随框架角的变化而变化; 稳定平台误差参数标定方法可以快速精确地辨识出稳定平台中的误差参数; 失调角线性误差模型补偿方法可以显著提高滚仰式半捷联光电稳定平台的视线指向测量精度。 本文的研究结果显著提高了稳定平台的视线指向测量精度,但文中主要针对稳定平台线性误差部分进行了标定与补偿分析, 后续需要研究模型简化、 环境和测量数据干扰等非线性因素的影响及其标定与补偿。
参考文献:
[1] 樊会涛, 闫俊. 自主化——机载导弹重要的发展方向[J]. 航空兵器, 2019, 26(1): 1-10.
Fan Huitao, Yan Jun. The Important Development Direction of Airborne Missile: Autonomization[J]. Aero Weaponry, 2019, 26(1): 1-10. (in Chinese)
[2] 樊会涛, 崔颢, 天光. 空空导弹70年发展综述[J]. 航空兵器, 2016(1): 3-12.
Fan Huitao, Cui Hao, Tian Guang. A Review on the 70-Year Development of Air-to-Air Missiles[J]. Aero Weaponry, 2016(1): 3-12. (in Chinese)
[3] 樊会涛, 张蓬蓬. 空空导弹面临的挑战[J]. 航空兵器, 2017(2): 3-7.
Fan Huitao, Zhang Pengpeng. The Challenges for Air-to-Air Missile[J]. Aero Weaponry, 2017(2): 3-7. (in Chinese)
[4] Rudin R T. Strapdown Stabilization for Imaging Seekers[C]∥2nd Annual AIAA SDIO Interceptor Technology Conference, 1993.
[5] 刘珂, 陈宝国, 李丽娟. 空空导弹红外导引头技术发展趋势及关键技术[J]. 激光与红外, 2011, 41(10): 1117-1121.
Liu Ke, Chen Baoguo, Li Lijuan. Development Tendency and Key Technology of IR Seeker for Air-to-Air Missile [J]. Laser & Infrared, 2011, 41(10): 1117-1121. (in Chinese)
[6] 吕常波, 丁海山, 花文涛, 等. 装调误差对滚仰式导引头视轴指向的影响分析[J]. 弹箭与制导学报, 2014, 34(5): 4-6.
Lü Changbo, Ding Haishan, Hua Wentao, et al. Analysison Influence of Installation Errors on Direction of Axis of Sight of Roll-Pitch Seeker[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(5): 4-6. (in Chinese)
[7] 赵明, 白杨, 刘慧. 导引头稳定平台指向误差建模与参数标定[J]. 红外与激光工程, 2013, 42(S2): 374-379.
Zhao Ming, Bai Yang, Liu Hui. Pointing Error Modeling and Parameter Calibration for Seeker Stabilized Platform [J]. Infrared and Laser Engineering, 2013, 42(S2): 374-379. (in Chinese)
[8] 王濤, 朱明超, 訚胜利, 等. 稳定平台轴系精度对视轴指向误差的影响分析[J]. 红外与激光工程, 2011, 40(11): 2265-2269.
Wang Tao, Zhu Mingchao, Yin Shengli, et al. Analysis of LOS Pointing Error Derived from Precision of Shafting in Stabilization Mechanism[J]. Infrared and Laser Engineering, 2011, 40(11): 2265-2269.(in Chinese)
[9] 王军平, 尚超, 吴军彪. 四元数法在光滑环系统坐标变换中的应用研究[J]. 航空兵器, 2011(3): 24-27.
Wang Junping, Shang Chao, Wu Junbiao. Application of Quaternion Method in Coordinate Conversion of Slick Chain System[J]. Aero Weaponry, 2011(3): 24-27. (in Chinese)
[10] 张良, 韩宇萌. 滚仰式半捷联稳定平台的神经网络自适应控制算法[J]. 测控技术, 2018, 37(6): 5-8.
Zhang Liang, Han Yumeng. A Neural Network Adaptive Control Algorithm for Roll-Pitch Semi-Strapdown Stabilized Platform [J]. Measurement & Control Technology, 2018, 37(6): 5-8. (in Chinese)
[11] Okamura K, Park F C. Kinematic Calibration Using the Product of Exponential Formula [J]. Robotica, 1996, 14(4): 415-421.
[12] 刘新新. 巡飞弹滚仰式导引头建模与末制导技术研究[D]. 南京: 南京理工大学, 2019: 7-20.
Liu Xinxin. Modeling and Terminal Guidance Technology of Roll-Pitch Seeker for Loitering Missile Systems [D]. Nanjing: Nanjing University of Science & Technology, 2019: 7-20. (in Chinese)
[13] 花文涛, 刘凯, 丁海山. 滚仰式红外导引头视线角速率提取方法研究[J]. 红外技术, 2015, 37(1): 63-66.
Hua Wentao, Liu Kai, Ding Haishan. Research on Roll-Pitch Infrared Seeker LOS Rate Extraction[J]. Infrared Technology, 2015, 37(1): 63-66. (in Chinese)
[14] 曾龙. 滚摆式导引头伺服稳定平台设计与研究[D]. 北京: 北京理工大学, 2016: 48-56.
Zeng Long. The Research and Design on Stabilized Platform of Roll-Pitch’s Seeker[D]. Beijing: Beijing Institute of Technology, 2016: 48-56. (in Chinese)
[15] 申帅, 张葆, 李贤涛, 等. 航空光电稳定平台质量不平衡力矩的前馈补偿[J]. 光学精密工程, 2017, 25(5): 1281-1290.
Shen Shuai, Zhang Bao, Li Xiantao, et al. Feedforward Compensation of Mass Unbalance Moment for Airborne Photoelectric Stabilized Platform [J]. Optics and Precision Engineering, 2017, 25(5): 1281-1290. (in Chinese)
Error Analysis and Compensation of Roll-Pitch
Semi-Strapdown Photo-Electricity Stabilized Platform
Zhao Yixin*, Cui Hao, Chen Xiaozeng, Ding Haishan
(China Airborne Missile Academy, Luoyang 471009, China)
Abstract: In order to improve the pointing accuracy of roll-pitch semi-strapdown photo-electricity stabilized platform, a method for error modeling and parameter calibration of stabilized platform is proposed. Based on the mechanical structure characteristics of the roll-pitch seeker, the main error sources of the stabilized platform are analyzed. Established the linear error model of the misalignment angle by using the coordinate transformation method and Taylor formula, and designed a method to improve the line-of-sight measurement accuracy of the stable platform by compensating the misalignment angle error. The least square method is used to design the calibration method of error parameters. The simulation results show that the error parameter calibration method can effectively calibrate the error parameters, and the method of compensating the misalignment angle error through the misalignment angle linear error model can significantly improve the line of sight pointing measurement accuracy of the stabilized platform.
Key words: stabilized platform; installation error; parameter calibration and compensation; roll-pitch seeker; least square method

