带两个服务等级的3台机半在线算法*
肖 满,丁 璐,张 怡
(云南大学数学与统计学院,云南 昆明 650000)
1 引言
在服务行业中,为了获得更多利益,服务商通常根据客户的消费水平将客户分为不同的服务等级,例如普通客户和VIP客户。VIP客户往往比普通客户享受更多的服务,即普通客户能享受的服务,VIP客户都能享受,而某些特殊服务只有VIP客户才能享受,因此需要制定一些策略使得服务效率更高。例如在酒店行业,酒店需要提供免费接机服务,一般情况下普通客户只能享受包车服务,而VIP客户可以享受专车服务,也可以与普通客户一起享受包车服务。若将服务的车辆看作机器,客户的需求看作需要加工的工件,预先给每台机器和每个工件安排一个服务等级标号,这就是一类带服务等级的排序问题。

带服务等级约束的排序问题最早由Bar-Noy等人[1]提出,并针对任意等级和m台同型机,他们首次给出了一个竞争比为e+1≈3.718的在线算法,当所有工件加工时间相等时,由该算法可得到竞争比为e≈2.718。Hwang等人[2]则研究了任意等级和m台同型机的离线情形,给出了一个近似算法,在m=2和m≥3时,分别得到竞争比为5/4和2-1/(m-1)。周萍等人[3]则研究了在3台同型机上带服务等级(最多有3个等级)的离线情形。

对于机器带有约束(Eligibility Constraints)的在线情形,在有2台同型机和3台同型机时,Lim等人[11]分别证明了由AW算法可得最优竞争比2和5/2。在有m台同型机时,相关研究成果可见文献[11]。在有2台同型机时,Lee等人[12]给出了一个最优在线算法HSF。Hou等人[13]研究了m台同型机的情形。

现有文献对2台机上带2个服务等级的情形研究已很充分,对3台机上带2个服务等级的半在线情形研究很少,而2台机上的半在线算法不能直接运用到3台机上,且3台机上不同半在线情形的算法并不通用,相反根据获知的工件信息不同,设计的算法差异会很大。因此,本文研究了一些带有2个服务等级约束,在3台同型机上的半在线排序问题,充分利用获知的部分工件信息,设计了有较好竞争比的在线算法。
2 问题描述
设有3台机器M1,M2,M3,一个工件序列S={J1,J2,…,Jn},机器和工件都有一个等级标号,工件一个接一个到达,只有安排好工件Jj,才能得知下一个工件Jj+1的信息(加工时间和等级)。工件Jj的加工时间记为pj,等级记为gj,一般将工件Jj记为(pj,gj)。 则对于任意工件Jj=(pj,gj),j=1,2,…,n,都有gj∈{1,2}。机器Mi的等级记为g(Mi),i=1,2,3,其中g(M1)=1,g(M2)=g(M3)=2。只有当gj≥g(Mi)时,工件Jj才能被分配给机器Mi加工,所有工件都必须被加工,且加工过程不可中断,工件Jj(j=1,2,…,n)被分配给机器Mi(i∈{1,2,3})后,不能取回再重新分配给其它机器。目标为极小化最大机器完工时间(makespan)。为方便叙述,使用三参数法将这个问题记为P(1,2,2)‖Cmax。

引理1工件Jj被分配后,最优解的目标值至少为LBj,j=1,2,…,n。
由引理1可得:
COPT≥max{T1,pmax,(T1+T2)/3}
(1)
3 P(1,2,2)|T1|Cmax
已知等级为1的工件加工时间之和为T1,本节给出了一个下界为3/2和一个竞争比为5/3的在线算法。
定理1对于P(1,2,2)|T1|Cmax,任意在线算法A的竞争比至少为3/2。

□
算法描述如算法1所示。
算法1H1算法
输入:工件序列S。
输出:工件序列S的一个分配方案。

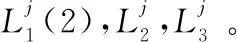
步骤3若gj=2,Jj按以下情况进行分配:
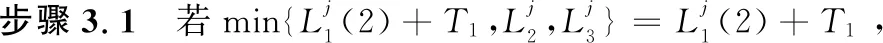

步骤4若还有新的工件到达,j=j+1,返回步骤2。
定理2对于P(1,2,2)|T1|Cmax,H1算法的竞争比至多为5/3。
证明由式(1)知COPT≥max{T1,pmax,(T1+T2)/3},下面对max{T1,pmax,T2-pmax}分3种情形进行讨论:
情形1max{T1,pmax,T2-pmax}=T1,则T1≥T2/2,且COPT=T1。由H1算法可知,所有等级为2 的工件将以贪婪原则全部分配给机器M2和M3,则任意时刻,M2与M3的负载之差不会超过pmax。因此,CH1≤max{(T2-pmax)/2+pmax,T1}。
若max{(T2-pmax)/2+pmax,T1}=T1,则CH1=T1,此时H1算法的分配达到最优。否则,
CH1≤(T2-pmax)/2+pmax≤T1/2+T1,
因此,(CH1)/COPT≤3/2。
情形2max{T1,pmax,T2-pmax}=pmax,则COPT=pmax。
情形2.1T1≥T2-pmax。由H1算法可知,在这种情形下,任意时刻,M2和M3中总有一台机器的负载不会超过T1,因此所有等级为2 的工件将以贪婪原则分配给M2和M3。则CH1=max{L2,L3}≤(T2-pmax)/2+pmax,因此,CH1/COPT≤((T2-pmax)/2+pmax)/pmax≤3/2。
情形2.2T1 CH1≤max{L1,L2,L3}≤max{(T1+ T2-pmax)/3+pmax,(T2-pmax)/2+pmax} 又 (T1+T2-pmax)/3+pmax≤ 2pmax/3+pmax=5pmax/3 且 (T2-pmax)/2+pmax≤3pmax/2 所以证得CH1/COPT≤(5pmax/3)/pmax=5/3。 情形3max{T1,pmax,T2-pmax}=T2-pmax。 pt≤(T1+T2-pmax)/3+pmax 若M1被分配了等级为2的工件,则由H1算法可知,在M1被分配等级为2的工件后,任意2台机器的负载之差不会超过Pmax。因此,CH1≤(T1+T2-pmax)/3+pmax,证得: CH1/COPT≤((T1+T2-pmax)/3+pmax)/COPT= ((T1+T2)/3+2pmax/3)/COPT≤((T1+T2)/3)/ ((T1+T2)/3)+(2pmax/3)/pmax=5/3 证毕。 □ 已知等级为2的工件加工时间之和为T2,本节给出了一个下界为3/2和一个竞争比为9/5的在线算法. 定理3对于P(1,2,2)|T2|Cmax,任意在线算法A的竞争比至少为3/2。 证明令T2=6,首先出现J1=(1,2),J2=(1,2),J3=(1,2),J4=(1,2)。 情形1M1没有被分配工件。若M2或M3至少被分配了3个工件,则出现最后1个工件J5=(2,2),在J5被分配后,可得CA≥3,COPT=2。 若M2和M3分别被分配了2个工件,则出现工件J5=(2,2),若J5分配给M2或M3,则不再有新的工件到达,此时,CA=4,COPT=2。 若J5分配给M1,则出现最后1个工件J6=(3,1),在J6被分配后,可得CA=5,COPT=3。 情形2M1被分配了1个工件。无论其余3个工件如何分配给M2和M3,出现最后1个工件J5=(2,2),在J5被分配后,可得CA≥3,此时COPT=2。 情形3M1被分配了2个工件。最后出现J5=(2,2),J6=(3,1)共2个工件,在这2个工件被分配后,则有CA≥5 ,COPT=3。 情形4M1至少被分配了3个工件。则出现最后1个工件J5=(2,2),在J5被分配后可得CA≥3,COPT=2。 因此,证得CA/COPT≥3/2。 □ 算法描述如算法2所示。 算法2H2算法 输入:工件序列S。 输出:工件序列S的一个分配方案。 步骤3若gj=2,Jj按以下情况进行分配: 步骤4若还有新的工件到达,j=j+1,返回步骤2。 定理4对于P(1,2,2)|T2|Cmax,H2算法的竞争比至多为9/5。 证明由H2算法可知,L2≤3T2/5,L1≤2T2/5+T1,令Jt=(pt,2)是分配给M3的最小工件。 情形1等级为2的工件都小于T2/3。假设L3>3T2/5,则L1(2)+L2<2T2/5,因为Jt分配给M3,则由H2算法可知,L2+pt>3T2/5,L1(2)+pt>2T2/5。若L1(2)=0,则pt>2T2/5>T2/3,与等级为2 的工件都小于T2/3矛盾。若L1(2)>0,则必有等级为2的工件分配给M1,由H2算法可知,分配给M1的任意1个等级为2的工件Js=(ps,2),有L2+ps>3T2/5。因此,L2+L1(2)>3T2/5,与L2+L1(2)<2T2/5矛盾,所以L3≤3T2/5。又由式(1)知,COPT≥max{T1,pmax,(T1+T2)/3},若CH2=L1,则: CH2/COPT≤(2(T1+T2)/5+3T1/5)/COPT≤ (2(T1+T2)/5)/((T1+T2)/3)+ (3T1/5)/T1=9/5 若CH2=max{L2,L3},则: CH2/COPT≤(3T2/5)/((T1+T2)/3)≤9/5 情形2等级为2的工件只有1个不小于T2/3。假设L3>3T2/5,则L1(2)+L2<2T2/5,由H2算法有L2+pt>3T2/5,L1(2)+pt>2T2/5。若L1(2)=0,则pt>2T2/5,因为等级为2 的工件只有1个不小于T2/3,所以pmax=pt。又Jt是分配给M3的最小工件,所以L3=pmax=pt。由H2算法可知,在这种情形,除工件Jt外,其它所有等级为2的工件全分配给了M2。因此,L1=T1,又L3>3T2/5>L2,且L3=pmax,所以CH2=max{L1,L3}=max{T1,pmax}。由式(1)知,COPT≥max{T1,pmax,(T1+T2)/3},所以此时H2算法的分配达到最优。若L1(2)>0,则必有等级为2 的工件分配给M1,由H2算法可知,L1(2)+L2>3T2/5,与L1(2)+L2<2T2/5矛盾,所以L3≤3T2/5。 由情形1可知,CH2/COPT≤9/5。 情形3等级为2的工件有2个不小于T2/3。假设L3>3T2/5,则L1(2)+L2<2T2/5,由H2算法可知,L2+pt>3T2/5,L1(2)+pt>2T2/5。若M3只被分配了工件Jt,则L3=pt,因为L3>3T2/5,则pt=pmax>3T2/5。因此,由H2算法可知,在这种情形,除工件Jt外,其它所有等级为2的工件全部分配给了M2。由情形2可知此时H2算法的分配达到最优。若M3至少被分配了2 个工件,又Jt是分配给M3的最小的工件,则L3≥2pt,可得: T2=L1(2)+L2+L3≥(L1(2)+pt)+ (L2+pt)>2T2/5+3T2/5=T2 是真假式,所以L3≤3T2/5。由情形1可得CH2/COPT≤9/5。 情形4等级为2的工件有3个不小于T2/3 (即等级为2的工件只有3个,且大小都为T2/3)。由H2算法可知,L1(2)=L2=L3=T2/3,因此,CH2=L1(2)+T1=T2/3+T1。若T1≤T2/3,此时H2算法的分配达到最优。若T2/3 因此,证得CH2/COPT≤9/5。 □ 已知等级为1的工件加工时间之和为T1,等级为2的工件加工时间之和为T2,本节给出了一个下界为4/3和一个竞争比为3/2的在线算法。 定理5P(1,2,2)|T1&T2|Cmax,任意在线算法A的竞争比至少为4/3。 证明令T1=1,T2=8,首先出现J1=(1,1),J2=(1,2),J3=(1,2)共3个工件。 情形1M1只被分配了J1,则最后出现J4=(3,2)和J5=(3,2),此时可得CA≥4,COPT=3。 情形2M1被分配了J1,J2和J3中的1个,则最后出现J4=(3,2)和J5=(3,2),此时可得CA≥4,COPT=3。 情形3M1被分配了J1,J2和J3,则最后出现J4=(2,2)和J5=(2,2),J6=(2,2),此时可得CA≥4,COPT=3。 证毕。 □ 本节算法由文献[14]中CMF(Common Machine First)算法修改得到,具体步骤如算法3所示。 算法3H3算法 输入:工件序列S。 输出:工件序列S的一个分配方案。 步骤3等级为2的工件Jj按以下情况进行分配: 步骤3.2若T2>T1,则按以下情形分配: 步骤4若还有新的工件到达,j=j+1,返回步骤2。 定理6对于P(1,2,2)|T1&T2|Cmax,H3算法的竞争比至多为3/2。 CH3/COPT≤max{(T1+T2)/2,pmax}/ max{T1,(T1+T2)/3,pmax}≤3/2 证毕。 □ 已知等级为1的工件与等级为2的工件加工时间之和为T,本节给出了一个竞争比为3/2的最优在线算法。 定理7对于P(1,2,2)|T|Cmax,任意在线算法A的竞争比至少为3/2。 证明令T=6,首先出现J1=(1,1),J2=(1,2),J3=(1,2)和J4=(1,2)。 情形1若M1未被分配J2,J3和J4,则出现最后1个工件J5=(2,2),在J5被分配后,可得CA≥3,COPT=2。 情形2若M1被分配了J2,J3和J4中的1个,则最后出现J5=(1,1)和J6=(1,2),在这2个工件被分配后,可得CA≥3,COPT=2。 情形3若M1至少被分配了J2,J3和J4中的2个,则出现最后一个工件J5=(2,2),在J5被分配后,可得CA≥3,COPT=2。 证毕。 □ 本节算法由文献[14]中CMF算法修改得到,具体步骤如算法4所示。 算法4H4算法 输入:工件序列S。 输出:工件序列S的一个分配方案。 步骤3等级为2的工件Jj按以下情况进行分配: 步骤4若还有新的工件到达,j=j+1,返回步骤2。 定理8对于P(1,2,2)|T|Cmax,H4算法的竞争比至多为3/2。 证明若T1≥T2,由H4算法可知,等级为2的工件将全部分配给M2,即L2=T2≤T/2,L3=0,此时CH4=T1达到最优分配。若T1 CH4/COPT≤max{pmax,T/2}/ max{T1,pmax,T/3}≤3/2 □ 本文研究了在3台同型机上,带2个服务等级的排序问题,考虑了4种半在线情形:(1)已知低等级工件加工时间之和;(2)已知高等级工件加工时间之和;(3)分别已知2个等级的工件加工时间之和;(4)已知总的工件加工时间之和。其中只有第4种情形得到了最优在线算法,在后续的研究中,可考虑前3种情形的最优算法,以及3台机上的其它半在线情形。
4 P(1,2,2)|T2|Cmax




5 P(1,2,2)|T1&T2|Cmax





6 P(1,2,2)|T|Cmax

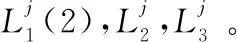


7 结束语

