全球气候变化模式和多基因遗传规划在逐日参考作物腾发量预报中的应用

姚顺秋，闫晓惠

(1.大连市庄河水利建筑勘测设计院，辽宁 大连 116400；2.加拿大渥太华大学工学院，安大略 渥太华 K1N6N5)

估算作物需水量是农业水利工程规划与设计中的关键环节[1- 2]，而作物需水量的估算主要是基于参考作物腾发量(ET0)的计算。因此，ET0的预报对水资源的精细化配置与管理工作具有非常重要的意义[3]。ET0的估算方法中较为简单的是直接估算法，即对历史ET0资料进行数据分析，并以此推测未来的ET0变化过程。近年来，全球气候变化显著，历史数据规律已经很难准确描述未来的水文气象变化趋势，因此直接估算法难以满足当前的精准化水资源管理要求。

间接估算法的原理是采用基于实际物理原理的ET0计算模型和气象预报数据进行ET0的计算，得益于气象预测能力的不断提高，间接估算法目前得到了大量的关注与研究。例如，刘梦等[4]采用天气预报数据对漳河灌区的参考作物腾发量进行了预报研究，徐俊增等[5]也对基于天气预报的参考作物腾发量预报方法进行了比较。近期，闫晓惠等[6]采用Penman-Monteith模型、全球气候变化模式和降尺度法对加拿大渥太华、温哥华等6个城市的逐日ET0进行了预报，取得良好的预报精确度。但是，该方法一方面对数据要求较高，另一方面也需要较为繁杂的降尺度操作，限定了其广泛的应用。随着人工智能与机器学习技术的不断进步，采用人工智能算法来推演模型成为重要的技术手段。近年来，闫晓惠等[7- 9]成功将人工智能与机器学习技术引入到不同的水资源相关应用中，且证明该项技术在水利领域中具有非常明显的优势。首先，采用机器学习技术代替人为分析可以大幅度节省人力成本；其次，人工智能算法不需要提供预设的模型结构，从而可以避免预设模型结构的不合理性；此外，该方法也可以深度挖掘变量之间的相互作用关系，从而可提供更为精确的模型[10]。在各类机器学习算法中，遗传编程在水利领域中具有广阔的应用前景，它的一个重要特点是可以提供一个明确的数学模型。多基因遗传规划(MGGP)是近期在传统的遗传编程算法上演变而来，相对于传统遗传编程方法，它具有精确度更高、复杂度更低等优点，因此具有非常大的发展潜力[7- 9，11]。

但据笔者所知，目前，基于多基因遗传编程和全球气候变化模式的ET0估算方法几乎没有被报道过。因此，本文旨在对该方法进行可行性研究与性能评测。首先采用大连市庄河地区2011年7月1日—2020年3月31日间的逐日最高与最低气温数据、基于Hargreaves模型计算了该地区与时间段内的逐日ET0值。分别采用本文新提出的方法(GCM-MGGP)、全球气候变化模式的原始数据法(GCM法)和全球气候变化模式与传统的遗传规划方法(单基因遗传规划；GCM-SGGP)对该ET0序列进行计算，并对各项结果进行比较分析，为ET0的预报工作提供新的方法与经验。

1 研究方法

1.1 气象数据

实测气象数据选取大连市庄河地区2011年7月1日—2020年3月31日共3197组数据的逐日最高与最低气温数据。日最高气温数据序列的最大值、最低值、平均值和中间值分别为35、-19、14.7、16°C；标准差、方差、峰度和偏度值分别为11.2、126.5、1.8、-0.3。日最低气温数据序列的最大值、最低值、平均值、和中间值分别为26、-23、5.3、6°C；标准差、方差、峰度、和偏度值分别为11.8、138.4、1.8、-0.1。

全球气候变化气象预测数据主要提取自MRI-CGCM3模式。该模式是在CMIP5(第五代耦合模式比较计划)框架下开发的全球气候模式，主要包含气温、降雨、海平面气压、风速和降雪5项气象因子。本文提取其中对应于庄河地区的模拟结果，其坐标为北纬39.6808°、东经122.9673°。在该数据中，日最高气温数据序列的最大值、最低值、平均值和中间值分别为33.3、-20.1、11.0、11.7°C；标准差、方差、峰度、和偏度值分别为12.0、142.9、1.9、-0.3。日最低气温数据序列的最大值、最低值、平均值和中间值分别为25.9、-23.6、5.3、5.8°C；标准差、方差、峰度和偏度值分别为12.0、144.7、1.9、-0.2。

1.2 Hargreaves参考作物腾发量模型

Hargreaves 模型可表示为[12]:

(1)

式中，T—日最高气温与最低气温的平均值，℃；Rs—太阳辐射，MJ/(m2·d)。

Rs可通过下式计算[13]：

(2)

式中，KRs—经验系数，对于内陆地区其值一般设定为0.16，而对于沿海地区其值一般设定为019；Tmax、Tmin—日最高和最低气温；Ra—地外辐射，MJ/(m2·d)。

Ra的计算公式为[14]:

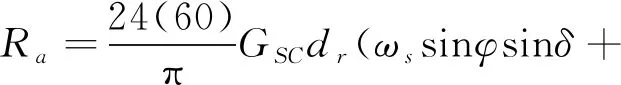
(3)

式中，GSC—太阳常数,取 0.0820;dr—日地相对距离;ωs—日落时角;φ—维度;δ—太阳偏磁角。

日地相对距离dr和太阳偏磁角δ的计算公式为：

(4)

(5)

式中，J—日序号。

日落时角ωs的计算公式为：

ωs=arccos(-tanφtanδ)

(6)

1.3 传统与多基因遗传规划

遗传规划是基于达尔文进化论和孟德尔遗传变异理论思想、参考生物演进过程而开发的一种可以构造算法与模型的算法。该方法可以随机产生模型种群，并对各模型进行评测，若不满足要求，则自动采用基因繁殖、基因突变、和基因交叉等运算来对种群进行改进，直至出现满足要求的模型。在传统的遗传规划算法中，一个模型染色体只包含有一个基因(因此也可称为单基因遗传规划)，但在多基因遗传规划算法中，一个模型染色体可以有多个基因，从而可以使得其精确度更高或复杂度更低。在本项目的模型训练过程中，选取的输入量分别为GCM最高气温和GCM最低气温，选取的输出量为实际的ET0值。因此，所得模型可以直接建立GCM模拟气温数据与实际ET0值之间的关系，而不需要进行ET0模型计算、降尺度分析、和地区修正等操作，因此采用训练后的模型进行ET0预报具有操作简便、易于上手的现实优点。

1.4 误差分析指标

采用均方根误差(RMSE)和决定系数值(R2)来量化预报值与实际值之间的误差，其公式分别为：

(7)

(8)

式中，xs—实测值；xm—模拟值。

2 研究结果与分析

2.1 基于GCM-MGGP法的ET0预报

将数据组随机分配为两个部分，分别为训练数据序列和验证数据序列。其中，训练数据占数据总量的80%，主要用于训练模型；剩余数据为验证数据，主要是当做为未知数据以评测所得模型的预报性能。图1呈现的为MGGP模型的训练演化过程。在第一代模型种群中，各模型为随机产生，因此其误差较大，RMSE值超过1mm/d，之后，MGGP算法利用演化运算来对模型进行改进，只需10代左右，模型种群的误差值变化幅度即已较小，说明运行更多的进化代数不再显著提高种群的精确度。因此，将最终的总进化代数设置为300即可满足要求。

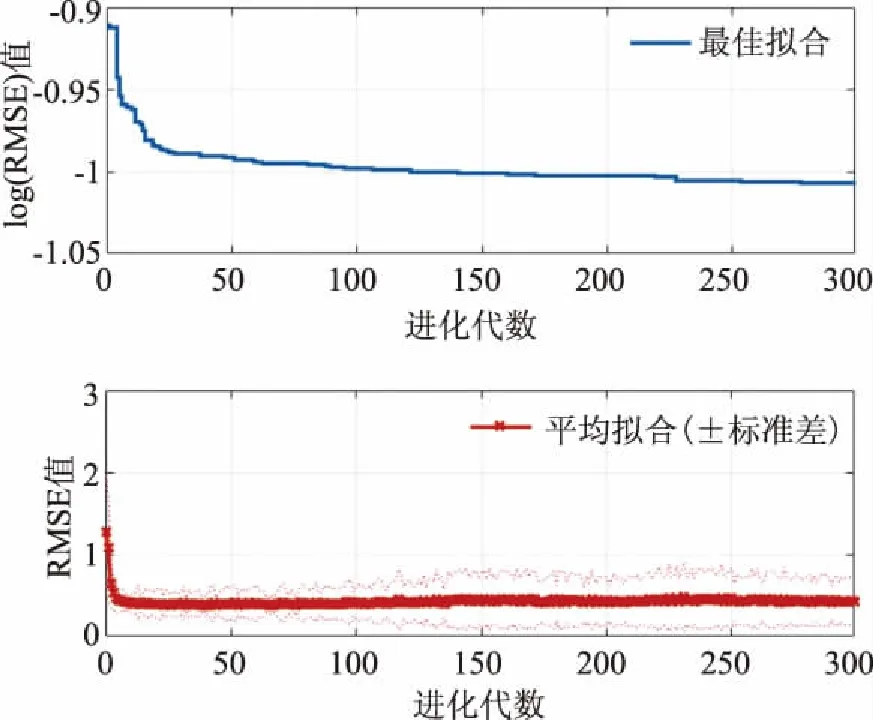
图1 MGGP模型的训练演化过程

每代种群包含500个模型，图2绘制的为最后一代种群中各模型的复杂度与性能指标值。判断一个模型的优劣一般要考虑精确性和简易性两个方面，而这两个方面却通常是矛盾的。本研究采用Pareto优化法，并将位于Pareto优化解曲线上的模型用圆圈表示。这些模型的特点是：在相同的精确度下，这些模型最为简易；而在同样的复杂度下，这些模型的结果最为精确。最终，选择这些模型中精确度最高的模型作为整个种群中的最优解。最优模型的树状结构呈现于图3中，其中x1代表日最高气温、x2代表日最低气温。

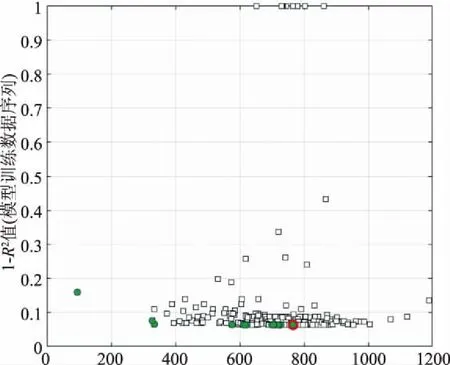
图2 MGGP模型种群中各模型的复杂度与性能值

应用该最优MGGP模型计算研究区域的逐日ET0值，并称之为“GCM-MGGP预报值”。图4对比了ET0的实际值与GCM-MGGP预报值。由图可知，GCM-MGGP数据与实际数据的变化规律基本保持一致。训练数据的RMSE值为0.365mm/d，R2值为0.936；验证数据的的RMSE值为0.364mm/d，R2值为0.938。RMSE值均较低，且R2值均较高，说明该方法可以提高满意的预报精确度。同时，训练数据序列与验证数据序列的误差水平非常接近，说明模型训练过程中的过拟合风险较低。

2.2 与GCM法和GCM-SGGP方法的比较

图5呈现了研究区域内逐日ET0的实际值与GCM法预报值的时间序列。由图可知，GCM法大体上可以准确地预报出数据的起伏变化过程，但是，较多的数据点误差较大。而且，多数误差较大的数据预报值低于实际值，不利于水资源管理的安全性。GCM法预报数据的总体RMSE值和R2值分别为1.099mm/d和0.76，因此，精确度较低。根据RMSE的关系可知，GCM-MGGP法相对于GCM法可以将误差降低约67%，成效显著。GCM-MGGP法可大幅度提高其预报精度的一个重要原因是它相当于自动增加了高精准度的数据降尺度与地区修正操作并考虑了变量之间深度隐藏的作用关系。

图6为逐日ET0的实际值与GCM-SPPG法预报值的对比散点图。图中实线为1∶1等值线。当散点接近于等值线时，说明该数据点接近于实际值，否则说明偏差较大。图6显示，大部分散点均较接近于实际值，说明该方法的预报结果较接近实际值。较多的点位于等值线的左上方，说明该方法倾向于高估实际的ET0值。训练数据的RMSE值为0.373mm/d，R2值为0.934；验证数据的的RMSE值为0.368mm/d，R2值为0.936。RMSE值均高于GCM-MGGP法的结果，而R2值均低于GCM-MGGP法的结果，说明GCM-MGGP法相对于GCM-SGGP法更为精确。此外，采用Smits与Kotanchek[15]的Expressional-Complexity法衡量所得模型的复杂度，得到GCM-SGGP最优解的复杂度为1797。如图3所示，采用MGGP法所得的模型中各个基因为低维度线性或非线性项，而这些项是通过线性方向进行组合，因此，模型的非线性维度随基因数的增加而倾向于降低，本例中最优模型的复杂度为766，远低于GCM-SGGP最优解的复杂度。因此，可以认为GCM-MGGP法相对于GCM-SGGP法不但可以提高预报精确度，也可以降低所得模型的复杂度。

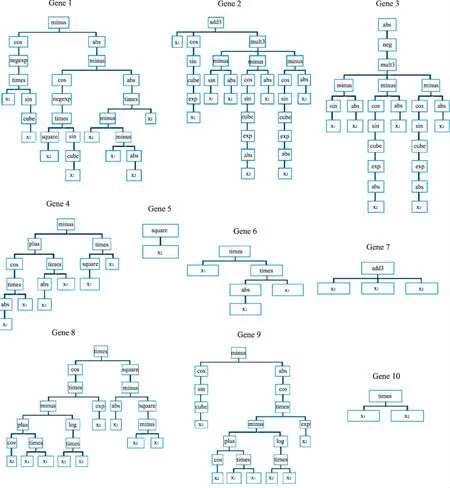
图3 最优MGGP模型的树状结构图

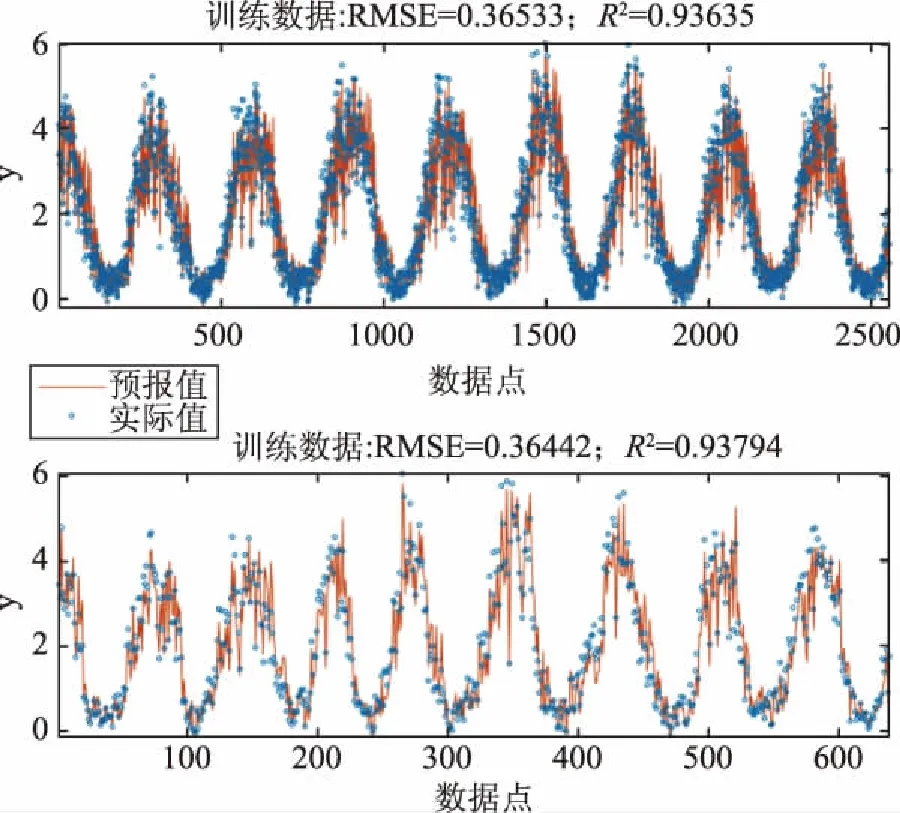
图4 ET0的实际值与GCM-MGGP预报值

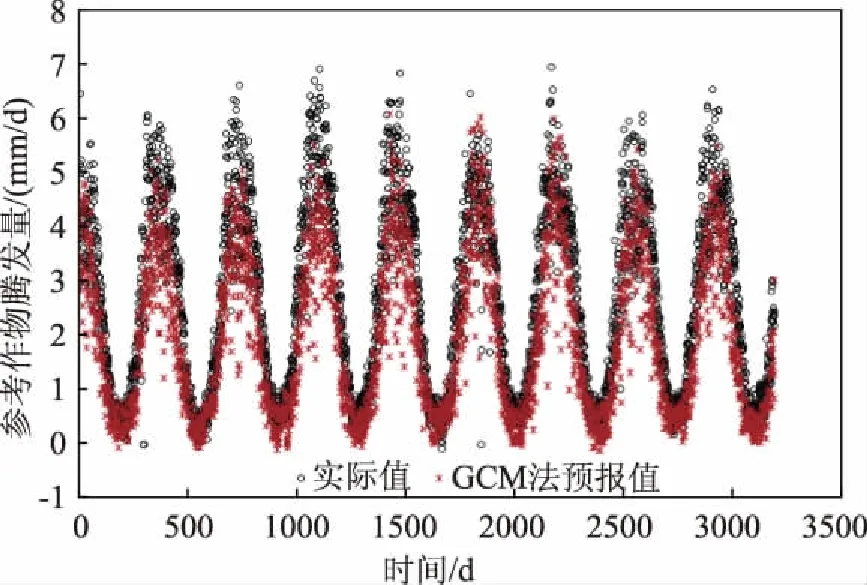
图5 逐日ET0的实际值与GCM法预报值的时间序列

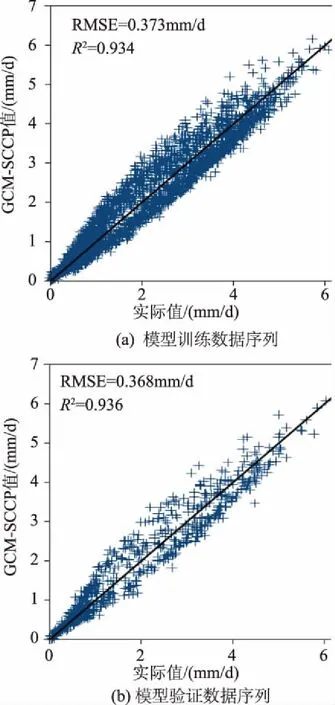
图6 逐日ET0的实际值与GCM-SPPG法预报值的对比散点图

3 结语

分别采用GCM法、GCM-SGGP法、和本文新提出的GCM-MGGP法计算了大连市庄河地区2011年7月1日—2020年3月31日间的逐日ET0值。结果显示，相对于GCM法，GCM-MGGP法可显著提高预报精确度。相对于GCM-SGGP法，GCM-MGGP法预报精度也有所提高，而其Expressional-Complexity复杂度可大幅降低。因此，GCM-MGGP法预报精确、模型简易，具有较好的发展潜力。受限于观测资料的不足，庄河地区实际ET0值的计算是基于Hargreaves模型，随着水文气象资料观测能力的提升，未来可以采用更符合现实情况的Penman-Monteith模型进行ET0计算，并采用类似方法训练出GCM-MGGP人工智能模型。此外，也可以将该方法在更多地区进行应用与验证，以进一步评测其性能。