发电电动机推力轴承弹性托盘应力及疲劳分析

黄建德，赵 锋，严天豪，崔运进，陈 骋，孙 逊

（华东桐柏抽水蓄能发电责任有限公司，浙江省天台县 317200）

0 引言

发电电动机的推力轴承支撑结构有弹性托盘、弹簧簇支撑等多种设计形式，这些支撑结构在推力负荷、热应力作用下产生的应力和变形对推力轴承的性能至关重要。弹性托盘结构简单、安装方便，但是受结构设计限制，其高度调节能力差，因此，每个弹性托盘的受力和变形的一致性不容易控制，电站运行时发现有单个弹性托盘断裂现象[12]。为防止类似故障再次发生，有必要研究弹性托盘的应力、变形和疲劳状况。抽水蓄能机组需要双向旋转，且运行工况变化特别频繁，因此结构设计必须要保证有更大的可靠性。

本文作者对过往国内推力轴承底部支撑结构研究的相关文献做了检索，文献[1]介绍了支柱式螺钉支承和弹性油箱支承时推力轴承主要受力和变形特点的理论公式计算方法，文献[2-3]用有限元方法研究了单瓦固定约束条件、双托盘支撑条件下的热弹流润滑计算得到的推力瓦瓦面压力场、温度场作用下轴瓦变形，文献[4]依据于过往的项目数据定义了推力轴瓦的变形判断和弹性托盘安全系数安全范围值，文献[5]采用实验的方法测量了老机组弹性托盘上的应力、温度和变形得出部分托盘疲劳破坏的结论，这些文献均采用了传统的静止工况计算方法，研究对象为单一产品类型且未涉及疲劳分析内容，未建立产品寿命周期设计考虑概念，对后续维护没有建立理论支持。

针对当前文献中有关水电设备承载件疲劳分析内容讨论较少的现状，提出有限元机械应力和热结构耦合分析相结合的推力轴承设计方法，通过有限元方法依据实际工况数据首先量化了某项目的弹性托盘支撑在力和热载荷下的变形应力数值，其次在明确了机械载荷为主要载荷基础上，利用Goodman疲劳预测方法综合了疲劳应力幅、材料机械性能等参数，对该项目弹性托盘高应力区域的高周疲劳寿命做了评估。

在疲劳分析过程中，本文通过调研疲劳分析的相关文献[6-8]和工业界相关成熟的实践[10]，找到解决当前材料实验参数不充分等制约疲劳分析工程实践因素的实践方法，把这些经过验证的经验参数取值和相应方法运用于某项目弹性托盘计算上，这些初步归纳的方法可以在后续被不断完善并运用于水电设备的其他重要零部件的机械疲劳校核评估工作中。

1 推力轴承弹性托盘所受工况及有限元模型的建立

在实际工程案例中，桐柏抽水蓄能电站的推力轴承采用了本文所述的方法设计校核，桐柏抽水蓄能电站自2005年投产至今，运行工况正常。

桐柏抽水蓄能电站项目的主要设计参数如下：推力轴承为单支点弹性托盘支撑结构，16块推力瓦，使用的弹性托盘外径280mm，内径260mm，托盘材料的屈服强度为1180MPa，抗拉强度在1370～1670MPa。

该项目推力轴承弹性托盘结构设计如图1所示，每块推力瓦下有一弹性托盘结构承载推力负荷。由于托盘及其受力为360°对称模型，为节约计算资源，在ANSYS软件中建立起应力和变形的四分之一模型分析结构。模型选用Solid226单元划分网格，该单元节点自由度除了空间位移UX、UY、UZ之外还有温度，采用“直接法”做有限元热结构耦合分析。上下托盘之间通过接触面传递载荷及热，因此，在交界处定义了接触对以耦合其交接处的位移和温度数值，采用了CONTA174和TARGE170单元定义接触面，接触面的接触特性定义为“Standard”允许接触面有滑移和脱离现象发生，摩擦系数定义为0.05。

图1 弹性托盘结构Figure 1 Spring disc structure

关于模型的加载和位移约束如图1所示，在有限元模型中90°分割截面上施加了对称面位移约束，在下托盘的底面施加25°的温度边界条件及全位移约束，在上托盘的顶部与推力瓦接合面上施加推力负荷及从推力瓦传来的热负荷。

对于弹性托盘而言，其主要载荷为来自推力瓦的垂直向压力。对于垂直压力的工况而言具体荷载组合列举如表1所示。

表1 推力负荷组合Table 1 Thrust load combination

根据上文的计算公式计算得到桐柏项目推力瓦的垂直承载力如表2所示。

表2 推力负荷各工况计算值Table 2 Calculated values of thrust load under various working conditions

对于热载荷，根据经验和文献查阅[13]做了预估：在上托盘与轴瓦底面接触处定义为50℃，根据其周边无明显液体流动及高低温差的热边界条件特点，仅考虑了热传导而忽略了对流和热辐射的热传递现象，上下托盘接触面采取热接触连接。

弹性托盘材料主要属性数据如表3所示。

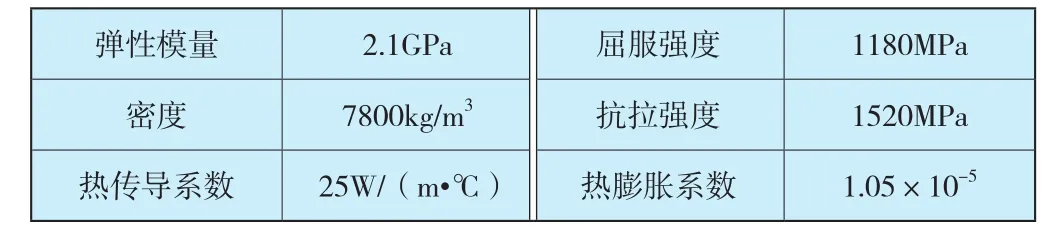
表3 弹性托盘材料物理参数Table 3 Physical parameters of spring disc material

根据上文罗列的工况和材料属性数据对有限元模型做载荷加载和材料参数定义，运行ANSYS软件计算。

2 有限元计算结果

对弹性托盘的传热模型做分析结构温度场热传导计算，结果如图2所示。

图2 弹性托盘温度分布Figure 2 Temperature distribution of spring disc

另计算了推力负荷在额定负载和瞬态荷载工况，得到各工况对应结构的变形如表4所示。

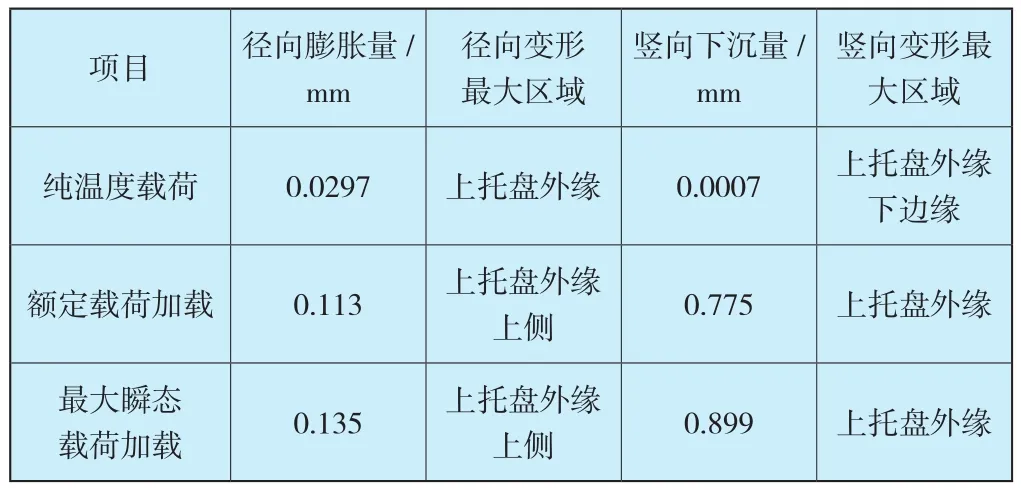
表4 各工况作用下结构最大变形Table 4 Maximum deformation of structure under various working conditions

从该表可以看到，热载荷引起的结构变形以径向膨胀变形为主：上托盘的变形是中心向上的微凸变形，上托盘边缘温度变形引起的竖向下沉量仅为受到额定载荷时下沉量的0.1%。另在热载荷下上托盘上的最大应力仅为17.7MPa，相对于推力负荷引起的应力而言热负荷的影响微乎其微，故在下文的计算中仅考虑推力载荷的影响，不同推力载荷下的下沉量计算结果总结如表5所示。

表5 各工况托盘下沉量Table 5 Spring disc subsidence under various working conditions

取上托盘与推力轴承轴瓦接触面边缘的下沉量、上托盘中心处下沉量为结果得出推力负荷和两处位移的拟合公式如图3所示，从所得的拟合受力变形公式可以得出结论：

（1） 上托盘的变形和载荷（单位：kN）的对应关系更接近于线性关系。

（2） 上托盘边缘处的变形很大程度源自托盘自身受力发生的弯曲变形。

对结构本身的应力做分析评估，选取最大瞬态推力负荷工况作为最恶劣工况计算结构的应力。应力（单位：Pa）分布如图4所示。

对这些应力的风险评估采用压力容器评价标准考核受力截面的安全性，对于这些高应力截面取路径做应力线性化后处理工作，路径定义如图4所示。

图3 弹性托盘受力变形关系拟合曲线Figure 3 Fitting curve of stress and deformation relationship of spring disc

图4 结构Von-Mises综合应力分布Figure 4 Von-Mises comprehensive stress distribution of structure

关于高应力区域在极限载荷下的评价，首先明确设计应力Sm的大小，根据规范定义，当SF为锻造或者轧制钢时取1.5，通过计算取最小值Sm为506.7MPa。对于截面上的应力分布，根据规范定义评判准则如下：

Pm+Pb≤K×Sm

式中Pm为应力线性化后的薄膜应力；Pb为弯曲应力；K为应力截面的形状系数。

根据规范定义当截面为正圆抗弯截面时取1.7，即861MPa。对两条路径上的应力线性化，得到结果如图5所示，红色线代表应力，紫色线代表Pm+Pb及薄膜应力和弯曲应力之和，淡蓝色线代表Pm，可以观察到两条路径上的应力值均没有超过861MPa的限值。

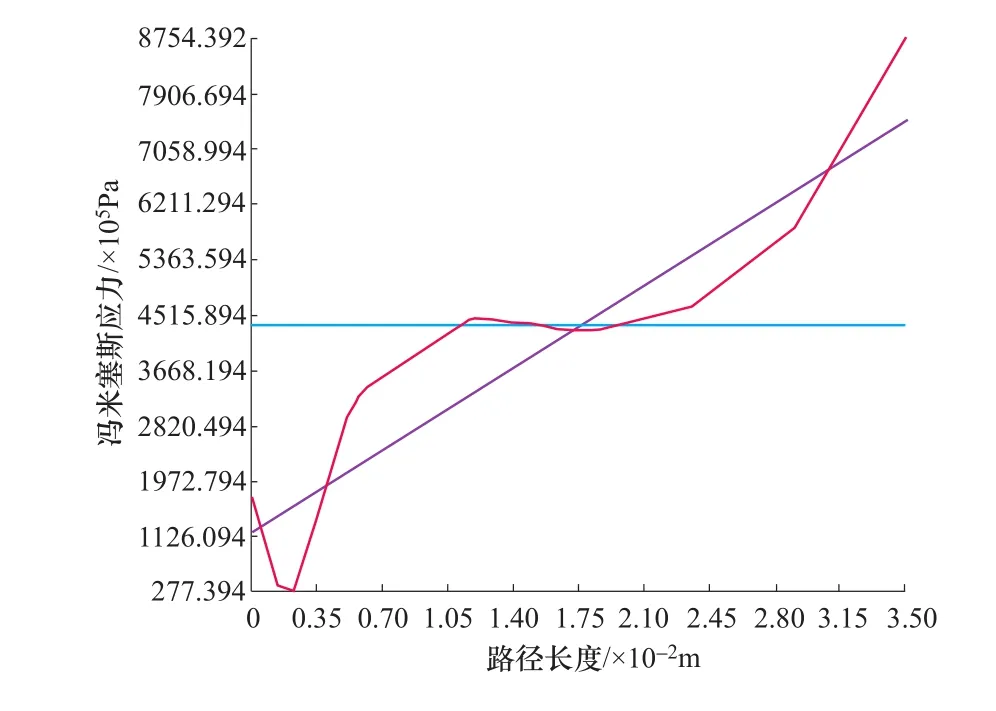
图5 路径A应力线性化结果Figure 5 Path a stress linearization results

图6 路径B应力线性化结果Figure 6 Path b stress linearization results

以上按照压力容器的评判标准做了应力线性化评估，且结构应力不超过屈服强度可以有效回避低周疲劳的风险。列出最大瞬态推力负荷时弹性托盘结构上所受的高应力区域应力值，3个高应力区的应力及结论如表6所示。

表6 弹性托盘高应力区域Table 6 High stress area of elastic tray

3 疲劳分析

上文采用了传统的静强度法根据压力容器理论，从截面的承载力角度评判结构应力低于限值是安全的，而缺乏对于结构承受的动态循环载荷造成的构件疲劳破坏风险的考虑，因此需要从疲劳分析的角度去补充评估结构安全性。

弹性托盘受到的载荷是如本文中列举的额定、瞬态等几个工况下交替变化的，鉴于弹性托盘承载推力轴承为水电设备重要的承载件，一旦失效必须停机检修维护工作麻烦，在过往水电站检修过程中确实有发现推力瓦托盘破碎现象[11-12]，因此对其疲劳寿命设计目标为“趋于无穷”，业内从工程实践角度来对钢质构件的“趋于无穷时设计寿命”的定义为循环次数为N=107。

关于目前工业界常用的几类疲劳寿命预测方法的等寿命曲线列举如图7所示，从原点出发的横纵坐标轴和相关评估标准的等寿命曲线构成的封闭区域为结构的目标疲劳寿命安全区间，本文将选用Goodman方法作为一个常规的工程实践办法对弹性托盘结构的疲劳寿命做评估。 Goodman方法是假设疲劳极限线经过对称循环疲劳极限点和拉伸强度极限点的一条直线，可以看到Goodman方法是这些方法中一个相对保守的评估方法。

图7 疲劳方法比较Figure 7 Comparison of fatigue methods

关于Goodman单向拉伸疲劳实验等寿命曲线的公式定义如式（1）所示，式中σa为疲劳点应力幅值，σm为疲劳点应力均值，Se为材料最大应力幅值，Su为材料的抗拉强度。

疲劳分析工程应用的一个难点在于疲劳实验的试件和实际构件在尺寸形状、表面加工质量、工作环境、平均应力大小及加载速率和频率等各个方面的种种差异而影响到的疲劳强度影响因子修正，参考文献[6]虽可找到相关影响因子的有代表性表格和公式数据但仍有其局限性。借鉴国外企业的成熟做法在疲劳分析流程上引入了构件疲劳强度衰减因子的办法来量化这种不确定性的影响：

式中KS为表面加工质量系数（≥1.0）；KC为表面涂层系数（≥1.0）；KE为材料强度衰减系数（≥1.0）；常规室温情况下的K可以取值1.5。

材料试件疲劳实验的结果是通过单项荷载加载实验做出的，而现实中结构受力疲劳是多轴应力分量的结果，多轴应力状态疲劳分析与单轴实验疲劳分析的转化对应关系是被深入研究的现实问题，查阅到文献[8]中归纳的把多轴应力转化为单轴应力的工程方法有以下3种：

（1） 最大主应力法，铁路工业ORE B12/RP17报告中给出了多轴应力状态向单向应力转化的方法并且其合理性已被广泛验证。

（2） 等效应力幅和等效应力均值，采用Mises应力计算均值和幅值，该方法在西门子等公司燃气轮机行业被广泛采用。

（3） 等效应力幅和SINES平均应力法，等效应力幅与方法2相同，sines等效平均应力为：

本文选用方法1做相关计算，基于最大主应变作为多轴疲劳寿命参量的公式如下：

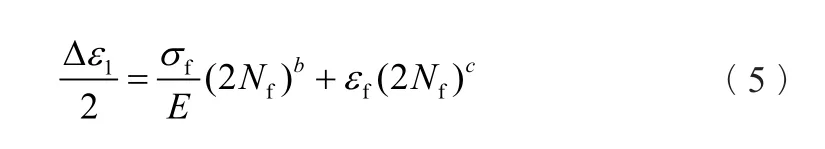
式中 Δε1为最大主应变；Nf为疲劳寿命；σf为疲劳强度系数；εf为疲劳延性系数，b为疲劳强度指数；c为疲劳延性指数；E为材料弹性模量。

另根据文献[9]，Se材料最大应力幅值在缺乏实验结果时可根据极限强度Su作简单估计，对于合金钢可定义Se为0.45的Su。采用主应力法评估结果计算弹性托盘在最大瞬态推力和最小载荷时的第一主应力，通过提取高应力区的节点结果做计算结果的筛选比对，找出4处位置的节点结果列在表7中。

根据表格中的数据绘制出Goodman疲劳分析图如图8所示，可以看到A、B、D三点落在Goodman的安全区域内，有接近无穷大的疲劳寿命，而C点即上托盘底面接触区高应力点落在区域之外，说明该处在若干多次应力循环之后不排除有疲劳破坏的可能性，可以在后续的检修工作中有意地观察该区域裂纹是否有发生。

表7 不同工况下结构高应力区应力数值Table 7 Stress value of high stress area of structure under different working conditions

图8 Goodman疲劳分析图Figure 8 Goodman fatigue analysis chart

值得一提的是，当前甄别出的疲劳破坏潜在区域并不意味着立刻判断该处失效，后续仍可以通过断裂力学模型计算来评估假如结构此处存在初始裂纹，该处裂纹扩展导致贯通失效的可能性及寿命预估，由于文章篇幅有限，在此不再展开叙述。

4 结论

本文通过对桐柏项目弹性托盘做有限元计算及采用Goodman疲劳分析方法实践，得出可以拓展到弹性托盘设计和后期维护的若干条结论如下：

（1） 弹性托盘的应力和变形主要受推力负荷影响，常规热载荷对综合受力和变形的影响极小。

（2） 通过计算结果找出了弹性托盘上托盘结构变形与承载力数值上的拟合关系，上托盘自身的抗弯变形占据了变形的60%以上比例，因此需确保上托盘的抗弯刚度设计。

（3） 用静态方法甄别了弹性托盘结构上的高应力区域的位置和截面的整体承载能力，鉴于弹性托盘为推力轴承关键承载部件，须确保结构应力不超过屈服强度避免低周疲劳的发生。

（4） 较常规的静态极限工况分析方法无法预判结构疲劳寿命的不足之处，本文在总结和借鉴了常用的疲劳参数假设和应力选取规则的基础上，采用了Goodman方法来有效的在设计阶段对结构的疲劳寿命做出评判，有助于量化了解结构各位置的疲劳风险，电站用户可结合发电电动机检修对缺陷的产生原因做评估及更换零部件。

（5） 通过本文的计算方法调研和应用举例，可以帮助设计人员在设计阶段从疲劳计算的角度对水电设备的核心承载构件做相应分析，水电设备企业在后续的工作中可以在该工程实践的基础上，就相应系数的定义和应力的处理方法做更深入的研究和程序开发，建立起一套成熟的计算规范指导实际工作。