高水头水泵水轮机无叶区压力脉动综述

徐连琛，刘德民，2，刘小兵，王小龙

（1. 西华大学流体及动力机械教育部重点实验室，四川省成都市 610039；2. 东方电机有限公司研究试验中心，四川省德阳市 618000）

0 引言

随着我国近几十年来经济的不断发展，对电力的需求不断地增大，近年来由于风电、光电等新能源大规模接入电网，电网调峰调频的需求不断增大，而抽水蓄能电站由于工作方式较为特殊，既能发电又能蓄能，同时与传统水电站一样，也具有启停快速和调节灵活的优点，能很有效的应付负荷的变化[1]，因而具有十分重要的研究意义。

作为火电和核电的补充，抽水蓄能电站自20世纪50年代开启了快速发展的进程，60～80年代进入了建设的黄金期[2]，作为调节电网运行的重要电站，广泛应用在世界各国。抽水蓄能电站在我国起步则较晚，1968年，国内第一座混合式抽水蓄能电站——河北岗南混合式抽水蓄能电站投入运行，截至2020年，国内抽水蓄能机组总装机容量突破3000万kW。

19世纪80年代，世界第一座抽水蓄能电站（组合式机组）在瑞士苏黎世建成，扬程为153m，随着技术的不断发展，可逆式机组逐渐成为主流的设计方案[1]。由于考虑到电站建设和运行过程中的经济性问题，当前修建的抽水蓄能电站普遍采用高水头机组，2014年投入运行的日本葛野川电站的最高扬程达到了782m[3]。在建的广东阳江抽水蓄能电站的最高扬程为705m。由于高水头抽水蓄能机组引水流道过长，且机组的设计偏向于径流式，无叶区的空间被压缩，又因为机组运行工况复杂，导致无叶区流动不稳定，无叶区压力脉动已经成为影响抽水蓄能电站运行稳定性的重要原因之一。

1978年投入运行的日本奥吉野电站机组的第一期三台水泵水轮机在运行一年后，所有机组的转轮都由于无叶区的压力脉动产生了疲劳裂纹[3]。Egusquiza等[4]报告了一个由无叶区压力脉动引起的大型水泵水轮机的故障调查。张河湾电站[5]由于水泵水轮机无叶区压力脉动造成了厂房和机组的振动。国内外研究表明，水泵水轮机的无叶区压力脉动是影响水泵水轮机运行稳定性的重要安全因素之一。因此，本文主要讨论了在实际工程和实验研究中的成果和结论，综合国内外研究人员的工作成果，其重点在于高水头水泵水轮机的无叶区压力脉动特性研究。

1 无叶区压力脉动机理研究

1.1 动静干涉作用涉及的流动现象

研究表明，无叶区的压力脉动主要是由动静干涉作用引发。不同转轮叶片流道中的压力分布是不同的，压力差的存在为机组的工作提供了力矩。在机组工作的过程中，压力场的变化具有一定的周期性。在静止坐标系中，同一旋转方向下的对称流场中，存在由于转轮旋转而引起压力流速的周期性变化，同时在活动导叶中也存在周期性的流态变化，因此将这种转轮与活动导叶的周期性扰动称为无叶区的动静干涉作用。动静干涉作用是旋转的和静止的叶栅之间的非稳态相互作用，其中导叶尾流及非设计工况下的旋转脱流与转轮叶栅发生的相互作用都是导致动静干涉的重要原因。

1.2 动静干涉作用机制

1.2.1 势流及尾迹对动静干涉的影响

Dring等[6]提出动静干涉可以分为两个部分，一是势流（无黏）相互作用，另一个是尾迹（黏性）相互作用。

势流干扰即叶栅之间存在的非定常位势干涉。旋转的转轮叶片通过静止的活动导叶的流场时，活动导叶流道的出流和转轮流道的入流相互作用，两者周期性叠加的压力场和速度场能够引起压力波动。Giesing等[7]提出当转轮叶片中一个叶片与导叶距离最近时，势流相互作用达到最强，对导叶的完全开启产生影响（见图1）。Lefcort等[8]提到，相对运动的相邻两叶栅之间的势流相互作用是由于叶片周围的环流和叶片周围的势流场（而非环流）导致的，这些势流场是由叶片的有限厚度（边界层厚度可包含在叶片厚度中）所引起的。叶片周围的势流场在叶片的上游和下游延伸，如果翼型之间的径向间隙近似的小于翼型弦长，则通过翼型的势流会导致上下游流动不稳定。

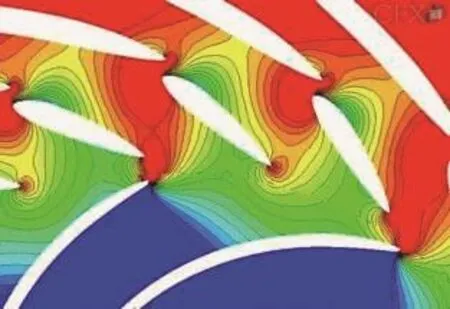
图1 势流相互作用最强时的压力场Figure 1 The pressure field when the potential interaction is strongest

对于黏性流动效应来说，蜗壳内流场流速的均匀性，导水部分的水流角度，脱流[9]以及尾迹作用都对动静干涉存在影响。

尾迹干扰是因为上游叶片尾迹进入下游叶片时，因被下游叶片截断而造成了尾迹切割，在多级叶轮机械内将呈多次交叉切割，形成叶栅后的脉动。Gallus[10]提到当翼型径向间距小于十分之一的翼型弦长时，势流干涉的作用才能达到尾迹干涉作用的效果，尾迹干扰效果随着翼型径向间距的增加而越来越强，而势流干涉的影响则越来越小， 尾迹由于对流作用存在且其衰减速度较慢，即使相隔很远也会存在尾迹的相互作用。因此，尾迹干涉成为研究人员研究的重点。尾迹对环栅的周期性冲击使得叶片表面产生压力脉动，是导致叶片振动以及无叶区压力脉动的主要原因之一。

尾迹效应是由于导叶本身存在而造成的流动损失，以及导叶叶片压力面和吸力面之间的压力梯度造成的。尾迹相互作用主要影响下游流场，其主要体现在无叶区和转轮叶片表面的低频压力波动，其主导频率为活动导叶尾迹频率及其倍频，压力波动的幅度沿流向逐渐减小。尾迹作用会导致在下游流道中产生涡旋分离和扩展，可以诱发结构振动。这些由涡引起的流动不稳定现象可以增强湍流耗散率以及能量耗散[11]。尾迹通过转轮叶片和活动导叶之间的交互运动产生的干涉形成周期性的尾迹结构，这些流动结构可以通过对流作用影响叶片的边界层，导致边界层结构的不稳定[12]。Hobbs等[13]以及 Capece等[14]通过试验研究尾迹的损失、宽度以及尾迹引起的下游叶栅流道内的非定常压力波动都会随着叶片负荷的增加而增加。杨彤等[15]提到尾迹周期性的通过叶片表面使得叶片升力系数波动幅值超过 5%，同时下游流道内的速度矢量波动增加几倍。Tsukamoto等[16]通过试验研究了动静干涉现象，结果表明导叶上监测点的压力随着叶频和高次谐波的基本频率而波动，最大值出现在导叶吸力面的前缘。Uzol等[17]和Chow等[18]通过PIV试验发现，尾迹—尾迹干涉和尾迹—叶片干涉会导致流动的不稳定，尾迹流动会被下游叶片切断，由于平均速度的差异，位于上游叶片的压力面的尾迹区比吸力面的尾迹区对流更快，因此尾迹的轨迹会产生间断，导致下游速度场的紊乱，增加了湍流强度。

1.2.2 动静干涉引起转轮振动的节径判断方法

Nicolet等[19][20]采用一维方法对水轮机的动静部件进行了水声模型的构建，分析了导叶和转轮的厚度，转轮叶片和导叶的波速以及转轮转频对动静干涉压力脉动的影响，通过研究发现由于转轮叶片旋转所产生的压力场和活动导叶尾迹造成的压力场的相互作用是动静干涉的产生原因，动静干涉作用会导致流体机械内部产生活动导叶与转轮叶片间的周期性激振，即径向振动模式和蜗壳中的压力波干涉。

由于高水头水泵水轮机的活动导叶较厚，导叶出口的尾迹对转轮叶片造成的水力激振力比较大。由转轮叶片和固定导叶之间的水力干涉引起的水力激励力使得转轮受到一个规律的周期性的激励，从而导致转轮的振动，转轮叶片每经过导叶尾流时就产生一次激振。

如图2所示，是一个有6个转轮叶片和20个活动导叶的水泵水轮机的动静干涉示意图。转轮叶片1和转轮叶片4首先被活动导叶1和活动导叶11的尾迹所激励。顺时针旋转6°之后，转轮叶片2和转轮叶片5同时被活动导叶4和活动导叶14的尾迹所激励，再旋转6°之后，转轮叶片3和转轮叶片6又同时被活动导叶7和活动导叶17所激励。由于总是两个转轮叶片被激励，转轮会发生一种径向振动[21]。

图2 动静干涉现象示意图Figure 2 Diagrammatic sketch of rotor-stator interaction

对于这种径向振动，Tanaka[4][22]通过理论和试验研究，开发了一个模型来确定高水头水泵水轮机的径向振动模式。当转轮叶片穿过导叶尾流时，会产生明显的水力激振，导致转轮的振动，提出公式（1）：

式中Zs——活动导叶数；

Zr——转轮叶片数；

k——节径数；

n，m——任意整数（一般n=1）。

压力脉动以如图3所示的模式旋转。

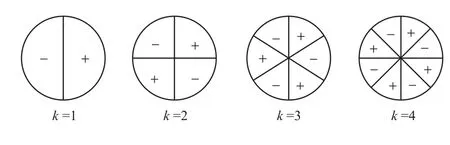
图3 压力脉动旋转模式Figure 3 Rotational mode of water pressure pulsation

对真机转轮的振动特性提出公式（2）：

式中fr——转轮在动静干涉作用下导致的激励振荡的振动频率；

N——转轮转频。

式中Nmr——水压振动的模式相对于转轮的转速。

式中fs——静止坐标系下因动静干涉作用发生水压脉动时的频率。

式中Nms——静止坐标系下水压振动的模式的转速。

Tanaka等[22]以及Kubota等[23]做了进一步的推导。由于受到转轮叶片旋转运动的影响，转轮进口和活动导叶出口的压力场在圆周方向上存在不均匀分布的现象，假设任意活动导叶流道的压力分布相同且任意转轮流道的压力分布也相同，此时在圆周方向上，导叶出口以及转轮进口的压力场具有周期性特征，傅里叶级数能够表示这种周期性变化 ［见式（6），式（7）］。

活动导叶出口圆周方向周期性压力变化（静止坐标系下）：

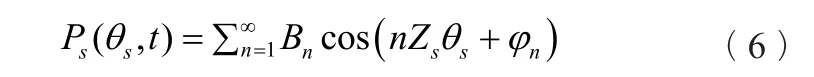
转轮进口圆周方向周期性压力变化（旋转坐标系下）：

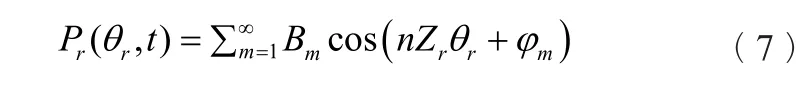
式中Ps——静止坐标系下活动导叶出口压力场；

Pr——旋转坐标系下转轮进口压力场；

m，n——谐波阶数；

Bn，φn——n阶谐波幅值和相位；

Bm，φm——m阶谐波幅值和相位；

θs，θr——静止坐标系和旋转坐标系下的角坐标。

两种不同的压力场相互干涉，在无叶区叠加产生的压力场可以表示为式（8）：

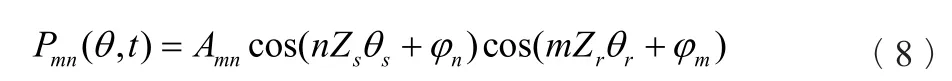
式中Amn——叠加合成的压力幅值。

进行三角恒等变化得：

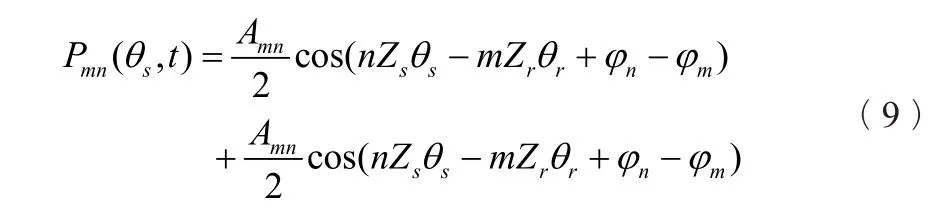
得到转动坐标系和静止坐标系的关系：

式中ω——转轮的角速度。

静止坐标系下，由势流干涉引起的无叶区压力脉动表示为：

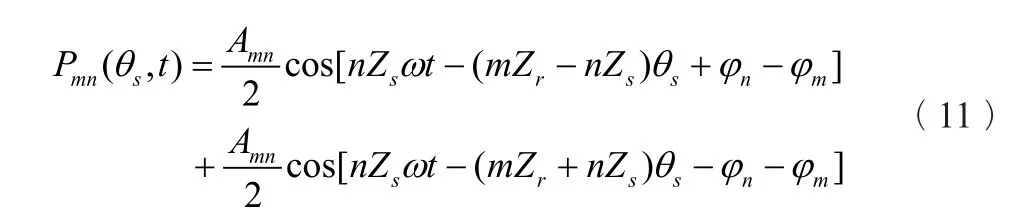
由此动静干涉作用而引发的压力场实际上可以表示为时间和空间的函数。

在此定义两个节径数k1和k2：

由于无叶区动静干涉产生的压力场受转轮转动的影响，圆周方向某个频率分量的压力分布随着时间的推移而旋转，其旋转角速度为：

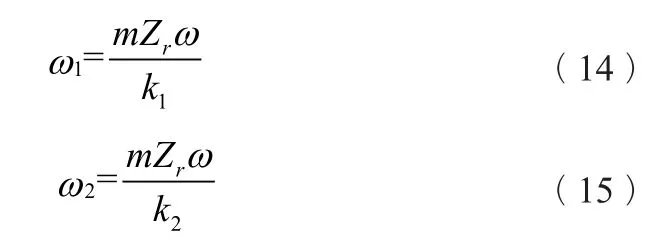
节径数k的符号决定了旋转方向，当k为正值时，ω的方向与转轮同向；反之，ω的方向与转轮反向。

转轮叶片数为偶数时，节径k的范围为0～Zr/2，转轮叶片数为奇数时，节径k的范围为0～（Zr-1）/2。强度随着谐波阶数m和n的增大而递减。

1.2.3 动静干涉的强度判断方法

影响水泵水轮机动静干涉作用的主要因素包括几何参数以及流动参数。几何参数如叶片数、导叶数、导叶与叶片的距离等，流动参数如转轮转频、流速、压力等。袁寿其等[24]提到采用式（16）判断动静干涉强度最方便。

式中——最大单位流量，m³/s；

——最优点单位流量，m³/s；

Qmax——最大流量，m³/s；

Qopt——最优点流量，m³/s；

Hmin——最危险点水头或扬程，m；

Hopt——最优点水头或扬程，m。

对于常规的水泵水轮机，随着导叶开度的增大，无叶区空间随之减少，在这两方面的同时作用下，会诱导压力脉动幅值的增大。

徐洪泉等[25]研究发现，无叶区压力脉动幅值是水泵水轮机所有位置中最大的，而且水轮机工况的压力脉动幅值要大于水泵工况。在水轮机工况下，压力脉动幅值在低水头工况时较大，压力脉动最大值出现在飞逸工况。水泵水轮机的无叶区压力脉动远大于常规的混流式水轮机。水泵水轮机无叶区压力脉动无论是在水泵工况还是水轮机工况，主频多数为叶片通过频率，这是由于高压侧压力分布不均的转轮高速旋转通过无叶区造成的，无叶区压力脉动的幅值随着压力分布的不均匀程度的增大而增大。水轮机工况转轮叶片进口脱流漩涡会导致高幅值的无叶区压力脉动。作者还指出水泵水轮机工况无叶区压力脉动幅值大的主要原因是运行范围的发电水头均低于最优工况水头。

1.3 其他原因对无叶区压力脉动影响的研究

国内外研究人员研究发现，除了动静干涉作用的直接影响之外，还有一些能导致或增强无叶区压力脉动的因素。如在机组切换工况的过程中：E. Vagnonia等[26]通过对水泵水轮机无叶区中旋转气—水环的研究，探讨了旋转气—水环对无叶区动静干涉的影响。提出旋转气—水环与运动的转轮叶片和静止的活动导叶的相互作用可以引发压力脉动，指出空化现象对无叶区的压力脉动存在影响。

刘骥生[27]对混流式水泵水轮机进行模型试验，用压力传感器对三种转轮在水泵工况和空化工况下的转轮高压侧及尾水管压力脉动进行了测量，并比较了三种转轮的压力脉动特性。实验表明在临界空化条件下压力脉动的幅度比非空化条件下高约30%～40%。提出了导叶开度，无叶区间隙，空化条件等对压力脉动的影响。

管子武等[28]对某水泵水轮机进行模型试验以及数值计算，发现对于5+5长段叶片转轮，在所有的工况点均出现了1倍转频的压力脉动，且在40%～50%负荷区间成为第一主频，文章中判断，产生1倍转频压力脉动的原因与尾水管的回流有关。

Staubli[29]等采用数值模拟分析得到水泵水轮机在“S”区运行时，转轮进口处存在的局部的涡结构是导致无叶区不稳定流动的根本原因。

Sun等[30][31]通过对不同导叶开度，不同导叶分布圆直径的水泵水轮机压力脉动进行分析，提出压力脉动与导叶开度有关，在最优开度下远低于其他开度。无叶区压力脉动的频率与导叶分布圆的直径存在一定的关系，但是与幅值的关系不大。

水泵水轮机在水轮机制动象限的旋转失速会引起活动导叶上的压力脉动，该旋转失速现象在水轮机制动工况区是很常见的现象，是引起飞逸工况点以上区域主轴强烈振动的主要原因[32]。

在以往的研究中，一般认为水是不可压缩的，但研究人员发现，对于一些小流量工况下的低频的压力脉动，数值计算对其幅值的预测往往差距很大，当考虑到水的压缩性时对这些压力脉动的预测往往能取得很好的效果。

Yin等[33]将水的压缩性加入到非定常流动的控制方程中，假设密度与温度无关。则水的状态方程为：

基于密度的连续性方程为：

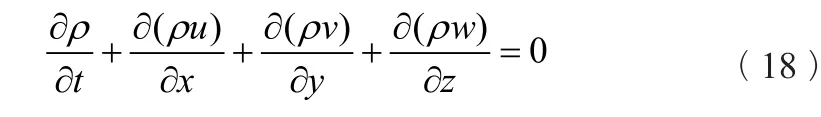
将密度代入式（17）得到关于压力的连续性方程：

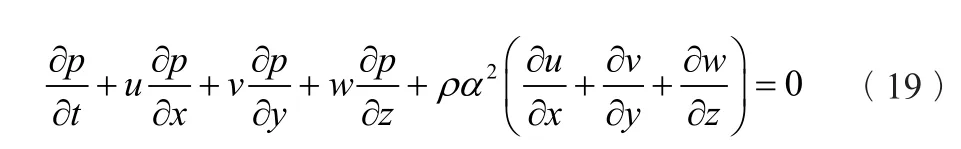
简化为：

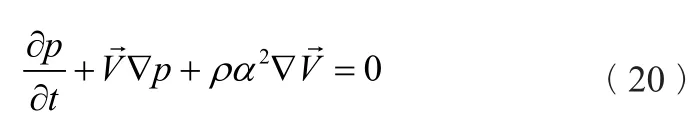
对于N-S方程，有：

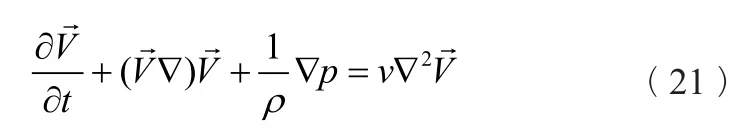
由于密度的变化很小，简化为：

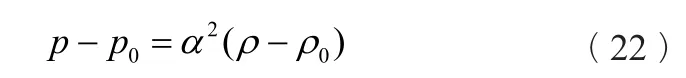
在工程中，水的压缩性通常用体积弹性模量表示：式

中ρ——水的密度；

ρ0——水的参考密度，1000kg/m3；

p0——水的参考压力，101325Pa ；

α——声速；

K——水的体积弹性模量，通常情况下为常数，K=2×109Pa。

Yin通过计算发现，考虑到压缩性后得到了与试验结果更加吻合的压力脉动幅值，而且可以更加精确的模拟低频压力脉动。

刘德民等[34]通过试验及数值模拟研究，发现对于高水头水泵水轮机，水的压缩性不可忽略。使用可压缩模型对水泵水轮机的压力脉动进行了计算，发现可压缩效应对水泵水轮机全域的压力脉动都有影响，压缩性对无叶区压力脉动的影响见图4。

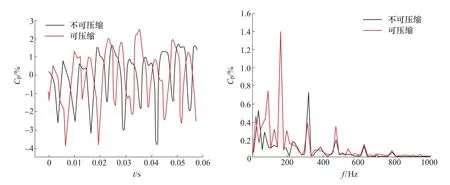
图4 压缩性对无叶区压力脉动的影响Figure 4 Influence of compressibility on pressure pulsation in vaneless space

Nicolet等[19]对某一水泵水轮机进行了水声建模，并对其进行仿真分析，发现动静干涉激励与蜗壳之间的水声共振对无叶区压力脉动的幅值以及相位的影响。

Xiao等[35]通过基于雷诺平均的N-S方程和SSTK-ω模型对某带有非同步导叶（MGV）的水泵水轮机模型进行了数值模拟，选取了三种不同开度的MGV布置方式，发现无叶区压力脉动明显减小。

2 动静干涉作用引起的结构振动现象研究

转轮相对于静止的蜗壳及导叶旋转会导致一些周期现象，他们叠加在流道中流体的平均流速和压力上，转速的变化引起的周期性特性会以单个频率的方式出现在频谱中，如果这个频率与结构中某个固件的固有频率相同，就会引发共振现象，又叫做相位共振现象。影响水泵水轮机的共振现象的主要因素和动静干涉一样，包括几何参数和流动参数，几何参数不再赘述，流动参数不同于动静干涉现象，在这里还要考虑波速。

袁寿其[24]文中提到了用下式评判相位共振：

式中M——马赫数；

α——波速， m/s；

Dsp——蜗壳沿着圆周流动轨迹等效的管道直径，m；

n——转轮每秒内旋转的圈数，r/s。

文中还提到了避免相位振动的标准：

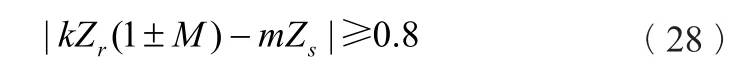
式中Zr——转轮叶片数；

Zs——导叶数量；

m——导叶通过频率下谐波的阶数。

由于在电站运行过程中，n一直在波动，且α无法准确确定，因此马赫数和避免振动的标准存在不确定性。

在式（27）的基础上提出了下式作为发生相位共振的条件：

式中ωe——压力模态的旋转速度；

v——带符号的节径，整数。

袁寿其[24]指出M*与M基本是倒数的关系。

Roth等[36][37]通过一套先进的仪器，对试验台上建立的水泵水轮机导叶的流固耦合问题进行分析，得到了导叶的振动可以局部的影响无叶区流体的压力脉动。而且导叶振动能够直接的影响上游和下游的压力脉动幅度，压力脉动的幅值随着与导叶距离的减小而增大。导叶的振动特性对压力脉动的幅度影响很大，他们的振幅能在导叶共振时下降50%，作者得出结论，振动之间所产生的相移可能是压力脉动幅度衰减的原因。

Tanaka[22]表明振动的激发力是由叶栅干涉引起的无叶区压力脉动产生的，Tanaka还提出，由于转轮的振动，导致静止部位存留的水从图3所示的“+”部分移动到“-”部分，由于水的附加质量效果较大，相对于在空气中的固有频率，水泵水轮机转轮的固有频率明显降低，k是较小的节径数时，下降的比例越大，当空气中的振动频率达到水中固有振动频率的两倍以上时，就有更大的可能性发生共振。

何玲艳等[21][38]根据Tanaka提出的公式，对某水泵水轮机的水力激振力频率及振型进行了分析，并结合水泵水轮机真机水头模型试验。发现k值较小的振型容易被激发且这些振型容易引发共振现象，也就是k=-2和k=+4的振型。

李启章等[39]对某抽水蓄能电站的水泵水轮机水泵工况下自激振动进行了研究，发现振动来源于导水机构的固有频率和转轮出口的压力脉动。水泵工况下转轮出口的水压是导致和维持振动的根源，与常规水轮机迷宫泄漏引发的自激振动在机理上相似。

3 无叶区压力脉动的试验研究和数值模拟

3.1 无叶区压力脉动的试验研究

试验研究是研究无叶区压力脉动的重要途径，一是对模型机或真机无叶区压力脉动的幅值频率等的影响因素进行研究，另外就是运用现代技术进行无叶区可视化的研究。各国研究人员对水泵水轮机中的压力脉动现象进行了大量的试验。

1974年，Grein等[40]对某型水泵水轮机的模型和原型进行测试，在流道内不同位置进行测量，得到了压力脉动的幅值及频率，并对得到的数据和预期的结果进行了讨论，分析了影响流道内不同位置压力脉动幅值及频率的因素。Vlad等[41]对某水泵水轮机在非设计工况下进行了试验研究，得到在最佳效率点时，压力脉动幅值主频为叶片通过频率，主要为无叶区压力脉动，在进入S形特征工况时，无叶区压力脉动明显增大。在低开度下，无叶区空间较大，流道内发生旋转流动分离，使得振动变得更加严重。杨建东等[42]对某原型混流式水泵水轮机在50%和75%满负荷进行突然甩负荷，得到当经过飞逸点进入水轮机制动区时，无叶区的压力脉动幅值最大。由于受到低频旋转失速的影响，无叶区压力脉动无量纲幅值范围达到了-1.0到1.0。还得到随着转速的增大，无叶区动静干涉频率对应的幅值也不断地增大，极值在飞逸时出现。任岩等[43]运用PIV技术对某模型水泵水轮机的转轮进行可视化研究，试验模型的主体部分均采用有机玻璃制成，采用数字粒子图像测速法对在不同工况下转轮内的流态特性进行研究，得到转轮叶片冲角和导叶开度对转轮内部流态的影响。

Zobeiri等[44]对某水泵水轮机模型的动静干涉现象进行了试验以及数值模拟研究，为减小无叶区的间隙采用了最大的导叶开度，结果显示在叶片通过频率下不同位置压力脉动幅值有所不同。在距离转轮最近的测点上，在同一部件上测到了最大的压力脉动幅值，表明该区域的动静干涉现象最严重。

刘燕生[45]对潘家口电站的水泵水轮机进行了模型试验，在四象限全特性试验过程中用压力脉动传感器进行了压力脉动的测量，结果显示水泵工况下无叶区压力脉动值最大，在同一牵引速度系数下，水轮机工况下无叶区压力脉动较大。在水泵制动工况中，无叶区压力脉动过大，超过了100%甚至达到180%（见图5）。得到水泵工况下的无叶区压力脉动频率主要是叶片通过频率，制动工况和反泵工况的压力脉动频率一般低于转频。

孙跃坤等[46]对某混流式水泵水轮机进行了开机过程中压力脉动特性的真机试验研究，结果表明在水轮机开机工况下，压力脉动随着开机进程不断减小，在导叶开启阶段为最大值，满负荷时压力脉动较小。在导叶开启阶段，见图6，压力脉动的主要来源是无叶区的动静干涉压力脉动。50%负载时，由于导叶开度较小，其压力脉动幅值最大。

在水泵开机过程中，排气阶段中压力脉动相对值达到最大，导叶开启阶段有压力脉动极值。在导叶开启和正常抽水阶段，如图7所示，动静干涉引起的无叶区压力脉动较大。

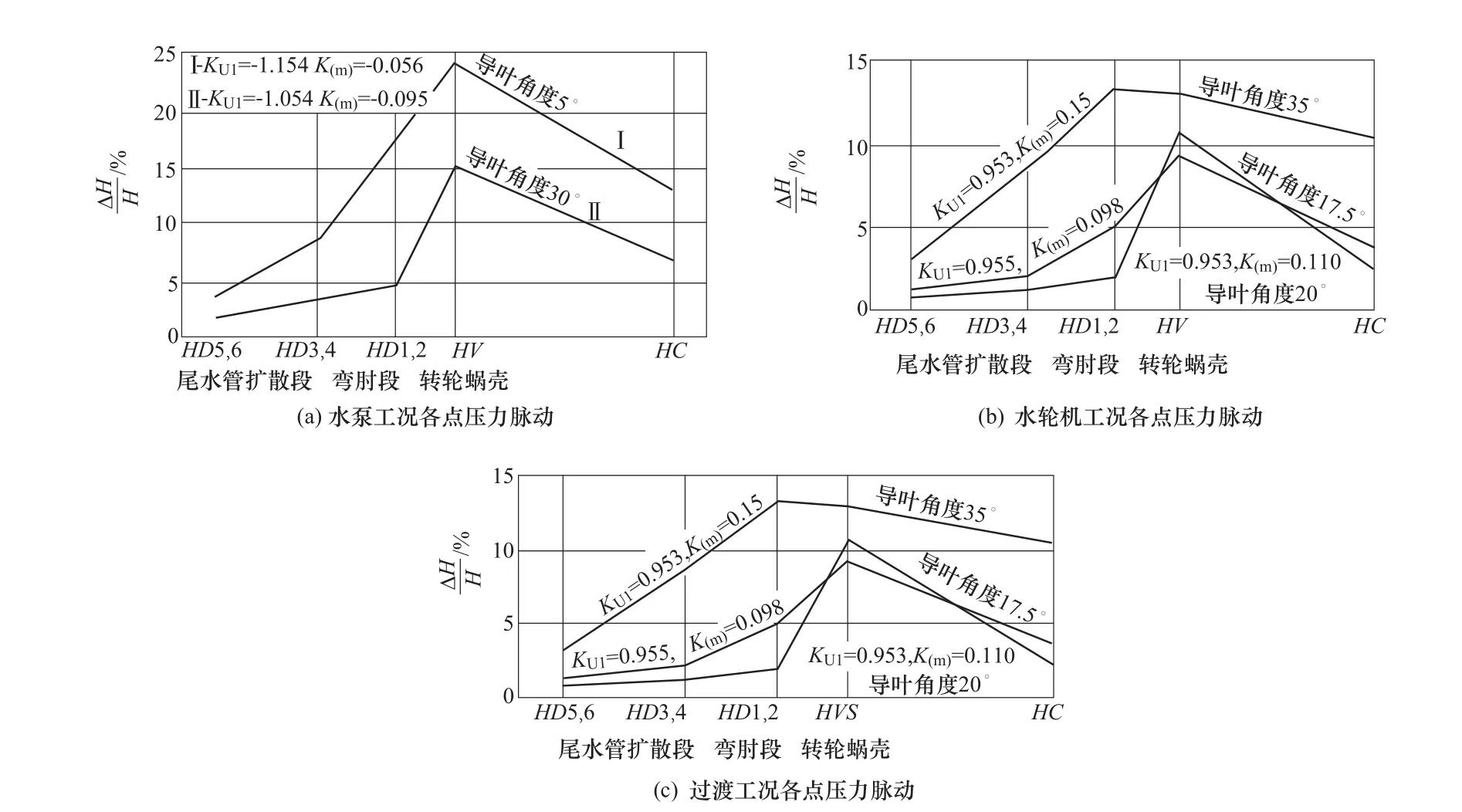
图5 不同工况下各点的压力脉动Figure 5 Pressure fluctuation of each point under different working conditions

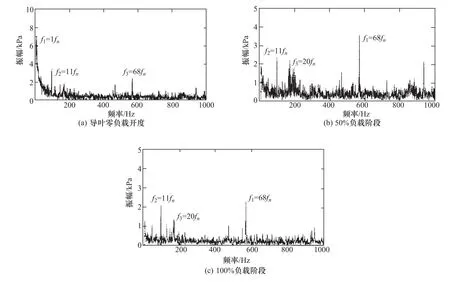
图6 水轮机开机过程压力脉动频域图Figure 6 Frequency domain diagram of pressure fluctuation during turbine startup

Gabriel等[47]通过PIV，LDV的方法对某水泵水轮机（见图8）无叶区的流场及压力场等进行了详细的试验研究。对小流量工况，最佳效率工况以及大流量工况对模型机的运行状态进行测试。

试验测量得到了湍流动能，二维瞬时空间速度分布以及无叶区流态分布，通过总压测量得到其压力波动信息，对水轮机工况和水泵工况下的动静干涉效应进行了分析，确定了该水轮机的最佳效率点。

国内外研究人员通过大量的试验，得到了许多关于不同工况下无叶区压力脉动幅值及主频变化规律等的研究成果，对无叶区压力脉动的产生机理何影响因素得到了初步的了解，为进一步研究无叶区压力脉动提供了坚实的基础。

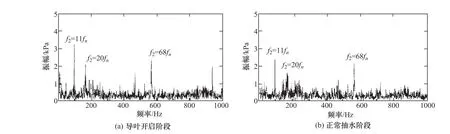
图7 水泵开机过程压力脉动频域图Figure 7 Frequency domain diagram of pressure fluctuation during pump startup

图8 水泵水轮机试验模型Figure 8 Experimental model of pump turbine

3.2 无叶区压力脉动的数值模拟研究

尽管在水力相似条件下模型试验中得到了无叶区压力脉动的某些结论，但一些结论可能只能在一定的范围内是可靠的，某些结论甚至存在争议。模型试验只能帮助人们认识无叶区压力脉动的外部特征，但无法得到流道内部全面的流动情况，为研究流道内部全面的流动情况，国内外研究人员引入了数值模拟的方法，对无叶区的压力脉动现象进行更加深入的研究。

湍流模型的选择对数值模拟的结果有着决定性的影响，因此对与无叶区压力脉动的数值模拟研究，选择合适的湍流模型显得十分重要。

目前应用于水轮机的流体动力学数值方法主要有：①解Laplace方程；②解雷诺平均 N-S方程（RANS）；③解瞬态 N-S方程（DANS）；④大涡模拟（LES）。

对于动静干涉的数值模拟研究主要基于三维非定常的CFD方法，动静部件通常采用滑移面模型，这种模型由于考虑到了动静之间相对位置和坐标系的变化，对非定常流动的模拟能够取得较为准确的效果，大量地应用于动静干涉的计算[48～53]。

Li等[54]使用SST K-ω模型对某混流式水泵水轮机模型进行了三维非定常数值模拟，分析了无叶区压力脉动的变化情况，得到第一主频和第二主频分别为18fn和9fn，主要来源为导叶和转轮叶片间的动静干涉，并分析了不同频率分量的压力分布和传播特性。计算结果与试验结果进行对比，其水头，扭矩，效率的差异均小于5%。

Huang等[55]以LES模型为基础，LES（大涡模拟）是一种求解大尺度的脉动运动的方法，对紊流中的压力脉动细节有良好的模拟效果。Huang提出了一种DCNM的模型，并对某离心泵的动静干涉现象进行了数值模拟，该模型对势流及尾流的模拟效果良好，对压力脉动频率的预测基本符合，但幅值较实测值低。

王正伟等[56]使用PNG K-ω模型对某水泵水轮机的动静干涉现象进行了数值模拟。计算结果显示，叶片转频和倍频是主要的压力脉动频率，计算结果与试验结论吻合良好。

李琪飞等[57]采用了基于单方程Spalart-Allmaras湍流模型的DES方法对某水泵水轮机的反水泵工况进行了数值模拟。计算得到了该水泵水轮机在反水泵工况下的压力脉动特性及传播规律，无叶区压力脉动主频为0.143倍转频，幅值达到100kPa左右，次频为叶频。无叶区复杂的压力脉动频率来源于两方面，一是动静干涉作用；二是在水轮机的旋转方向下，水泵方向出口的水流与活动导叶的碰撞导致的脉动增加，是水力机组的主要激振源之一。该模型成功的捕捉到了无叶区的中高频压力脉动，以及锥管内旋涡结构引起的低频压力脉动，与试验结果相差不大。

通过以上不同的模拟方法与计算模型，不难看出对于无叶区压力脉动的计算方法有很多，与试验结果的对比也都在允许范围之内，在以后的研究工作中，应当根据条件选择适合的湍流模型以及模拟方法，以得到更加准确的数值模拟结果。

4 抑制无叶区压力脉动的方法

由于无叶区压力脉动对于水泵水轮机及电站的稳定运行都存在影响，各国研究人员对改善无叶区压力脉动的方法进行了许多的研究。主要是分为在结构设计上降低脉动和在运行过程中降低脉动。

王焕茂等[58]总结了2009年以来哈尔滨电机厂在混流式水泵水轮机转轮长短叶片研究的进展。进行了长短叶片转轮的模型试验以及数值模拟，长短叶片的水泵水轮机无叶区压力脉动幅值相对常规叶片有较大降低（见图9、图10）。

图9 叶片数不同的转轮在水泵工况下的无叶区压力脉动Figure 9 Pressure fluctuation in vaneless space of pump operating condition with different blade number

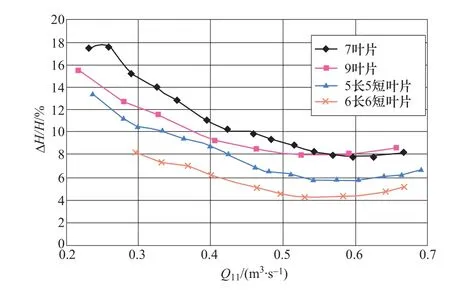
图10 叶片数不同的转轮在水轮机额定水头下的无叶区压力脉动Figure 10 Pressure fluctuation in vaneless space of turbine operating condition with different blade number at rated head

赵永智等[59]通过对20个活动导叶和22个活动导叶的两个水泵水轮机模型进行CFD计算，发现增加活动导叶的数目有利于提高水泵水轮机机组的稳定性，改善了无叶区的流动状态，有效降低了无叶区压力脉动的幅值。

川本一俊等[60]通过对三种导叶厚度或高度不同的水泵水轮机模型进行试验，提出提高导叶高度可以有效地降低无叶区的压力脉动，导叶高度提高40%时，无叶区压力脉动幅值降低了20%～30%。

陈元林等[61]通过数值模拟研究对几种不同设计方案的水泵水轮机进行了比较，采用面积变化规律更为平缓的转轮轴面流道和轴面流线方向相距较远的叶片高低压边轴面位置能够使压力脉动的相对幅值降低，增加转轮叶片数也可以降低压力脉动的相对幅值，模拟中发现随着叶片数的不断增加，压力脉动相对幅值降低的幅度不断减小。文章中还指出，随着导叶分布圆直径D0和转轮高压侧直径D的比值D0/D1的增加，无叶区压力脉动的幅值会明显减小。在同一导叶分布圆直径D0下，适当增大转轮相对低压侧直径D2与转轮高压侧直径D1的比值D2/D1，能够减小无叶区压力脉动的相对幅值。

Hongjuan Ran等[62]通过对某高水头水泵水轮机的两种转轮进行了数值模拟研究，发现使用扭曲的叶片有助于减小无叶区的压力脉动。白利等[63]对五个具有不同转轮高压边倾角的转轮进行了对比，提出在水轮机额定工况下，大的正倾角转轮可以降低无叶区压力脉动的幅值，小流量工况下。负倾角转轮可以降低无叶区压力脉动的幅值，综合考虑后提出小负倾角转轮对降低无叶区压力脉动的幅值最有利。Zhu[64]等，Xuhe W等[65]，Ma等[66]通过试验及数值模拟的方法，发现倾斜的转轮叶片对正常运行工况下及S形特征工况下的无叶区压力脉动具有抑制效果。

赵英男等[67]在某抽水蓄能电站水泵启动过程中进行了压力脉动试验，采用压水启动的方式，用压缩空气压低转轮处的水位，由于在转轮室排尽空气的瞬间产生了较大的压力脉动，建议在启动过程中完全排尽空气之前开启导叶。

钱忠东等[68]对混流式水轮机非同步导叶下的压力脉动进行研究，发现非同步导叶可以降低无叶区的低频压力脉动，但由于改变了原有的动静干涉特性，形成了新的振源，无叶区高频压力脉动有所增强。

Xiao等[35]，李琪飞等[69]，发现非同步导叶可以减小无叶区的压力脉动，通过对不同布置方案的比较，发现集中分布预开导叶比等间隔分布预开导叶的优化效果要好，能更有效的缓解机组的振动。水泵水轮机在小开度启动时，预开导叶可以有效缓解机组振动。郭雷等[70]提出非同步导叶的使用会影响导叶周围的脉动特性，压力脉动的在吸力面一侧较大，在压力面一侧偏小。

根据以上研究人员的研究，在以后的工作中必须在设计阶段考虑无叶区压力脉动的问题，对转轮叶片，导叶等的结构进行优化。并且在运行过程中，考虑各瞬态条件对无叶区压力脉动的影响。

5 结论

本文中根据国内外学者对于高水头水泵水轮机的压力脉动现象的研究进行了总结，得出以下结论：

（1） 无叶区的压力脉动主要是由于动静干涉现象引起。

（2） 水泵水轮机的几何参数和流动参数对无叶区压力脉动影响很大，应当在设计阶段对几何参数进行优化，对工况切换中的各瞬态阶段的流动不稳定现象进行预防以降低无叶区的压力脉动。

（3） 无叶区压力脉动的主频为叶片通过频率，无叶区的低频压力脉动来自尾水管回流等因素的影响。

（4） 对无叶区压力脉动应当继续深入对水的弱压缩性，空化等影响因素的研究。继续深入研究压力脉动引起的共振现象。