基于机器学习的原油管输能耗预测方法研究

徐磊 ，侯磊 *，李雨 ，张鑫儒 ，白小众，雷婷 ，朱振宇 ，刘金海，谷文渊，孙欣

1 中国石油大学(北京)机械与储运工程学院，北京 102249

2 中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室，北京 102249

3 国家管网集团北方管道有限责任公司锦州输油气分公司，锦州 121000

*通信作者, houleicup@126.com

0 引言

原油是重要的战略储备物资，主要通过铁路、水路、公路和管道4种方式运输。其中，管道运输因其运量大、封闭安全、易于管理等优点而被广泛应用。原油管道是将油田生产的原油输送至炼厂、港口或铁路转运站，具有管径大、输量大、运输距离长、分输点少的特点[1]。我国原油管道2020年的规划里程为32 000 km，2025年在此基础上要新增15.63%的里程。目前，我国所产原油80%以上为凝点较高的含蜡原油和黏稠的重质原油，输送过程耗能很大[2]。其中，泵机组的电耗是总能耗的主要部分，通过对泵机组电耗预测，能够做出一些关键决策，如能耗目标设定、批量调度和机组组合。依据能耗预测时间间隔长短，可分为短期预测、中期预测和长期预测，三者分别是指一天到一周、一周到一月、一月到一年的时间间隔[3]。本研究的能耗数据是以天为间隔进行采集的，因此，可视为短期能耗预测。

在实际管输过程中，能耗相关数据存在信息冗余、噪声干扰及非线性等特征，加大了预测难度。近年来，随着软计算技术的快速发展，机器学习方法已在能耗预测领域中得到广泛应用，该方法具有较强的容错性，较好的预测性能[4-6]。图1统计了2000年1月至2020年6月机器学习方法在能耗预测领域所发表论文的数量趋势，数据来源于Web of Science数据库。通过统计分析可得，机器学习方法在能耗预测领域的研究呈现逐年递增的趋势。随着“智慧管道”概念的提出，姜昌亮[7]、黄维和[8-9]、宫敬[10-11]、张劲军[12]、吴长春[13]、董绍华[14-15]等众多行业学者围绕智慧管道开展了大量研究工作，以数据驱动为依托的机器学习方法在油气管道行业的应用与发展势在必行[16-22]。

图1 机器学习方法在能耗预测领域发表论文数量Fig. 1 Number of papers occupied by machine learning method in the field of energy consumption prediction

在油气管输行业，若干学者对基于神经网络的油气管道能耗预测展开了相关研究。ZENG[23]利用神经网络对成品油管道电耗进行预测，并与线性回归和支持向量机展开对比，研究表明，所提出的神经网络模型有助于批次调度和能耗目标的设定。吴倩[24]提出一种基于BP神经网络的原油管道能耗预测方法，研究表明，与线性回归和灰色模型相比，建立的模型预测精度较高，适用于预测多种原油管道的耗电量和耗油量。温馨[25]将神经网络、支持向量机和极限学习机分别用于成品油管道能耗预测，研究表明，神经网络学习能力强、收敛能力强，拥有较高的预测精度。侯磊[26]利用BP神经网络建立输油管道能耗预测模型。预测结果表明，该模型预测偏差不超过4%，为输油管道能耗预测提供了一种新思路。高山卜[27]建立基于改进的BP神经网络原油管道能耗预测模型，得到该模型的误差在3%以内，且模拟值能够反映真实值的变化趋势。林冉[28]以某条输油管道几年来输量及生产油耗、电耗数据为基础，用人工神经网络的方法建立了管道输量与生产油耗、电耗的预测模型。分析表明，该模型的计算结果相对偏差在±5%以内，满足工程实际需要，能够用该模型来预测热油管道的生产油耗和电耗。

但以上方法对数据非线性和数据噪声考虑均不够充分，预测精度仍有一定的提升空间。图2～4统计了各类机器学习方法在能耗预测领域的应用。通过调研可得，智能优化算法和数据分解技术已被运用到风能、太阳能、核能等领域，用来解决数据非线性难以准确拟合、数据噪声难以高效去除的问题，但在油气行业运用甚少[29-32]。因此，本研究提出一种数据分解算法(CEEMDAN)、改进粒子群优化算法(IPSO)和反向传播神经网络(BPNN)相结合的混合预测模型。采用自适应噪声完整集成经验模态分解(CEEMDAN)去除冗余噪声，提取原始数据的主要特征，采用IPSO优化反向传播神经网络。结合国内3条原油管道，对提出的模型展开准确性评价。

图2 能耗预测领域的基准模型统计Fig. 2 Statistics of benchmark models in the field of energy consumption prediction

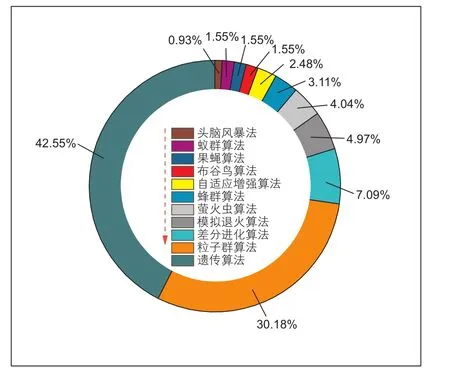
图3 能耗预测领域的优化算法统计Fig. 3 Statistics of optimization algorithms in the field of energy consumption prediction

图4 能耗预测领域的分解算法统计Fig. 4 Statistics of decomposition algorithms in the field of energy consumption prediction

1 基本方法

1.1 自适应噪声完整集成经验模态分解

实际现场采集的数据通常含有噪声，常规方法无法提取数据的主要特征。前人学者对此做了诸多研究，Huang[33]提出经验模态分解(EMD)方法将原始信号分解为多个内涵模态分量(IMF)，但模型和EMD无法很好的融合。针对此问题，Wu和Huang[34]提出集成经验模态分解(EEMD)方法，EEMD在稳定性方面有明显的改善，但很难完全抵消所增加的噪声。为了提高EEMD的性能，Torres[35]提出一种高级的自适应噪声完整集成经验模式分解算法(CEEMDAN)。CEEMDAN算法不仅能够解决EMD中模态混合的问题，而且通过加入成对白噪声，可以高效消除噪声，实现较好预测效果。因此，CEEMDAN算法作为一种实用的数据预处理工具，能够提高预测性能。

1.2 反向传播神经网络

人工神经网络(ANN)目前被广泛应用于各行业。其中，神经元是人工神经网络的基本处理单元，在输入节点处接收非线性信息，经内部处理后在输出节点处生成响应[36]。反向传播神经网络(BPNN)典型的三层前馈神经网络结构如图5所示。在反向传播神经网络中，神经元分层排列，包括输入层、隐藏层和输出层。人工神经网络将多个神经元相互连接，每个连接都有相应的权重。假设Wij是神经元i和j之间的连接权重，Xi是神经网络的输入向量，则两个连续层(k-1，k)的神经元j的输出值由公(1)式确定

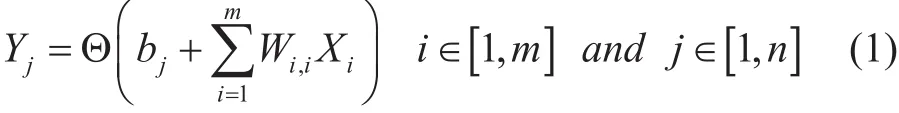
其中bj是阈值，Θ是激活函数，m是k-1层中神经元的数量，n是k层中神经元的数量。

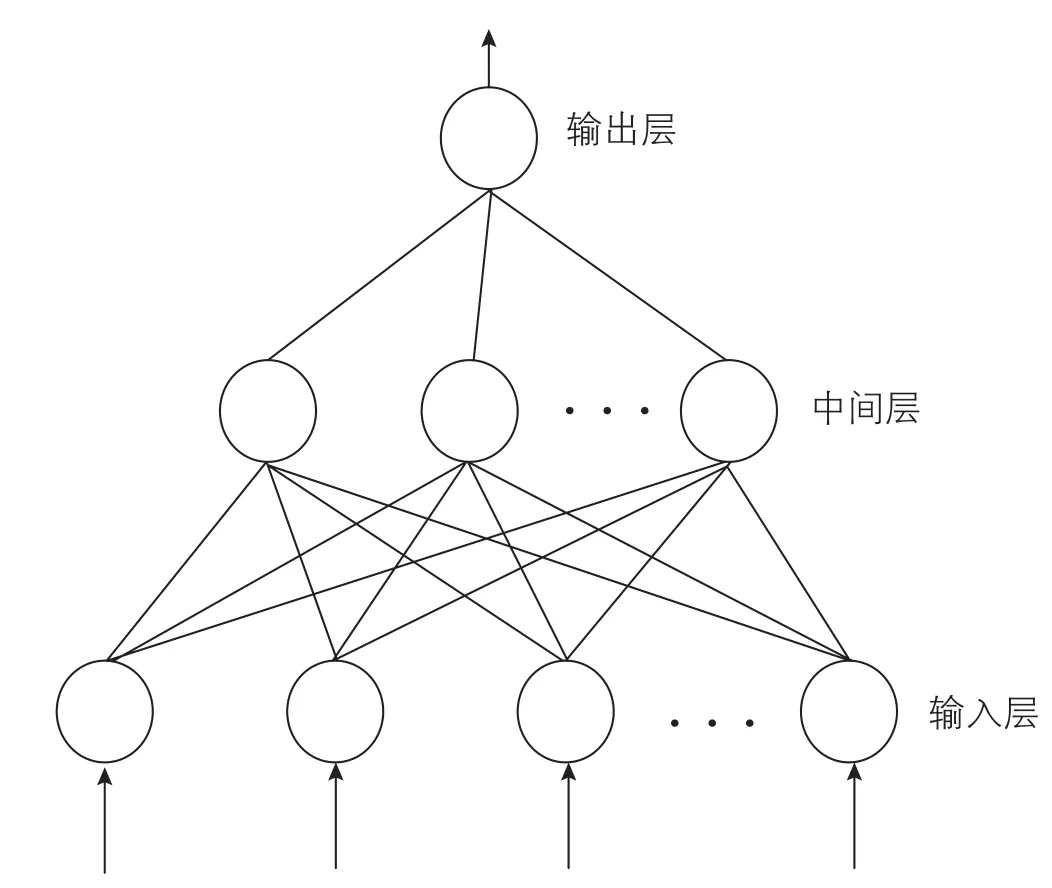
图5 三层前馈神经网络结构图Fig. 5 Structure diagram of 3-layers feed-forward neural network

1.3 改进粒子群算法

粒子群优化算法最早是由Eberhart和Kennedy[37]于1995年提出，能够解决复杂约束优化问题，同时又有较快的收敛速度。然而，传统的粒子群优化算法有时会陷入局部最优，因此提出改进粒子群优化算法(IPSO)来解决该问题。改进粒子群优化算法基于分布函数确定粒子位置，与传统的粒子群优化算法相比，改进粒子群优化算法需要调整的参数少，工作效率高、不容易陷入局部最优[38]。根据改进粒子群优化算法，计算种群的最佳位置如下：

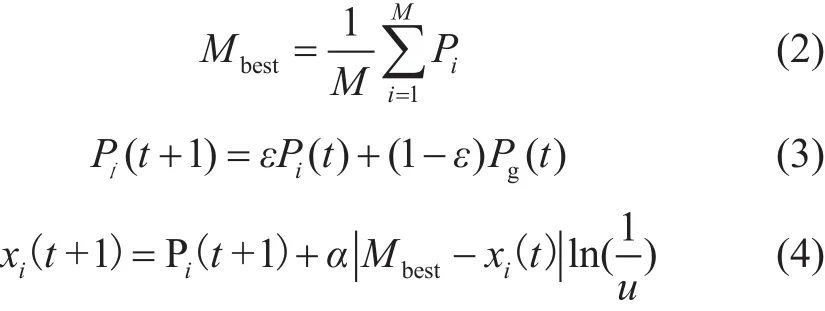
其中Mbest表示粒子的平均历史最佳位置，M是粒子群的大小，Pi是第i个粒子的历史最佳位置，Pi(t)是在第i个粒子在时间t的最佳位置，Pg(t)是在时间t的全局最佳位置，xi(t)是第i个粒子在时间t的位置，α是创新参数，值不大于1，ε和μ为在(0，1)之间的均匀分布。结合式(3)和等式(4)，可得到后代粒子的位置。

1.4 分层抽样方法

本研究生产数据来源于东北3条原油管道，记为A、B、C，以天为周期，采集2019年01月01日至2019年6月29日的数据，共计180组数据，管道A的部分数据如表1所示。在这项研究中，对于输入参数的选取需要满足两个条件，参数是变量且与电耗间存在相关性，因此，选取管输过程中的排量、平均进压、平均汇压、平均出压、平均泵出、平均进温、平均汇温、平均出温、地温、下站进压和下站进温等11个参数作为预测模型的输入参数。电耗是预测值，所以选取电耗作为输出参数。

训练集和测试集按4:1的比例进行划分。由于传统的随机抽样方法可能会导致测试集的分布规律与原始数据集分布规律有较大偏差，使预测结果不客观。因此，考虑采用分层抽样方法来划分数据集[39-40]。在原油运输过程中，输量对电耗影响最大，根据输量的分布规律可知，某些特定范围内的数据量较少，采用抽样时可能会遗漏该范围内的数据，为了保证每一数据范围内的数据都能够按比例被抽取，因此，依据数据的分布规律，将采集的数据划分为4个区间。以管道A为例，两种抽样方法得到的测试集与初始样本的偏差如表2所示。3条管线的随机抽样和分层抽样的平均绝对百分比误差(MAPE)见图6。对于A、B、C管道，随机抽样的MAPE分别为26.44%、19.20%、17.46%，分层抽样的MAPE分别为2.16%、2.16%、1.05%。结果表明，分层抽样得到的测试集与初始样本有较好的一致性。因此，本文采用分层抽样来划分训练集和测试集。

表1 管道A的部分数据Table 1 Partial data of Pipeline A

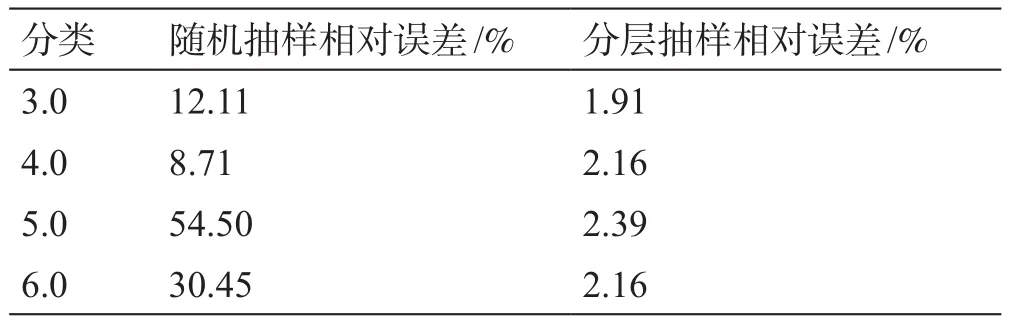
表2 基于管道A随机抽样和分层抽样的平均绝对百分误差Table 2 Mean absolute percentage error of random sampling and strati fied sampling based on pipeline A

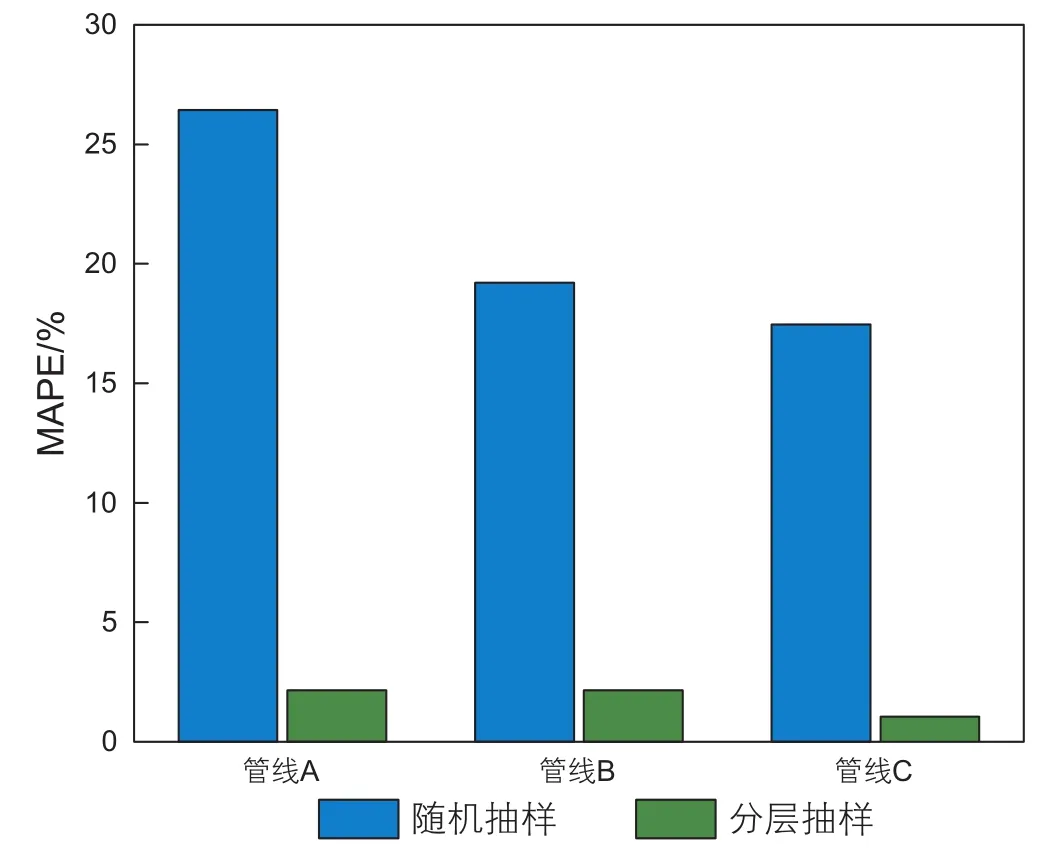
图6 3条管线随机抽样和分层抽样平均绝对百分比误差Fig. 6 Mean absolute percentage error of random sampling and strati fied sampling based on the 3 pipelines

2 预测模型框架

根据分解技术(CEEMDAN)和改进粒子群算法的BP神经网络(IPSO-BPNN)建立混合预测模型。采用CEEMDAN去除冗余噪声，提取原始数据的主要特征；采用IPSO拟合非线性特征，优化BPNN网络结构。结合国内3条原油管道，对比机器学习方法和SPS能耗预测模块，对所提出混合模型(CEEMDAN-IPSO-BPNN)的预测效果进行准确性评价，混合预测系统的建立流程如图7所示。

3 预测结果分析

实验过程通过Python 3.6.6语言实现，处理器为Intel Xeon E5-2643 v4，计算机内存为96.0 GB。以管道A为例，CEEMDAN-IPSO-BPNN混合模型的主要实验参数如表3所示。将CEEMDAN-IPSO-BPNN混合模型与主流机器学习方法和SPS能耗模块的预测性能分别展开对比，全面评价CEEMDAN-IPSO-BPNN的预测性能。

3.1 精度评估指标

通过大量文献调研，选取相对误差(RE)、决定系数(R2)、平均绝对百分误差(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE)、泰尔不等式系数(TIC)、分数偏差(FB)、预测结果统计1(U1)、预测结果统计2(U2)和方向精度(DA)10个主流指标来评价模型的预测性能[41-44]，表达式如表4所示。

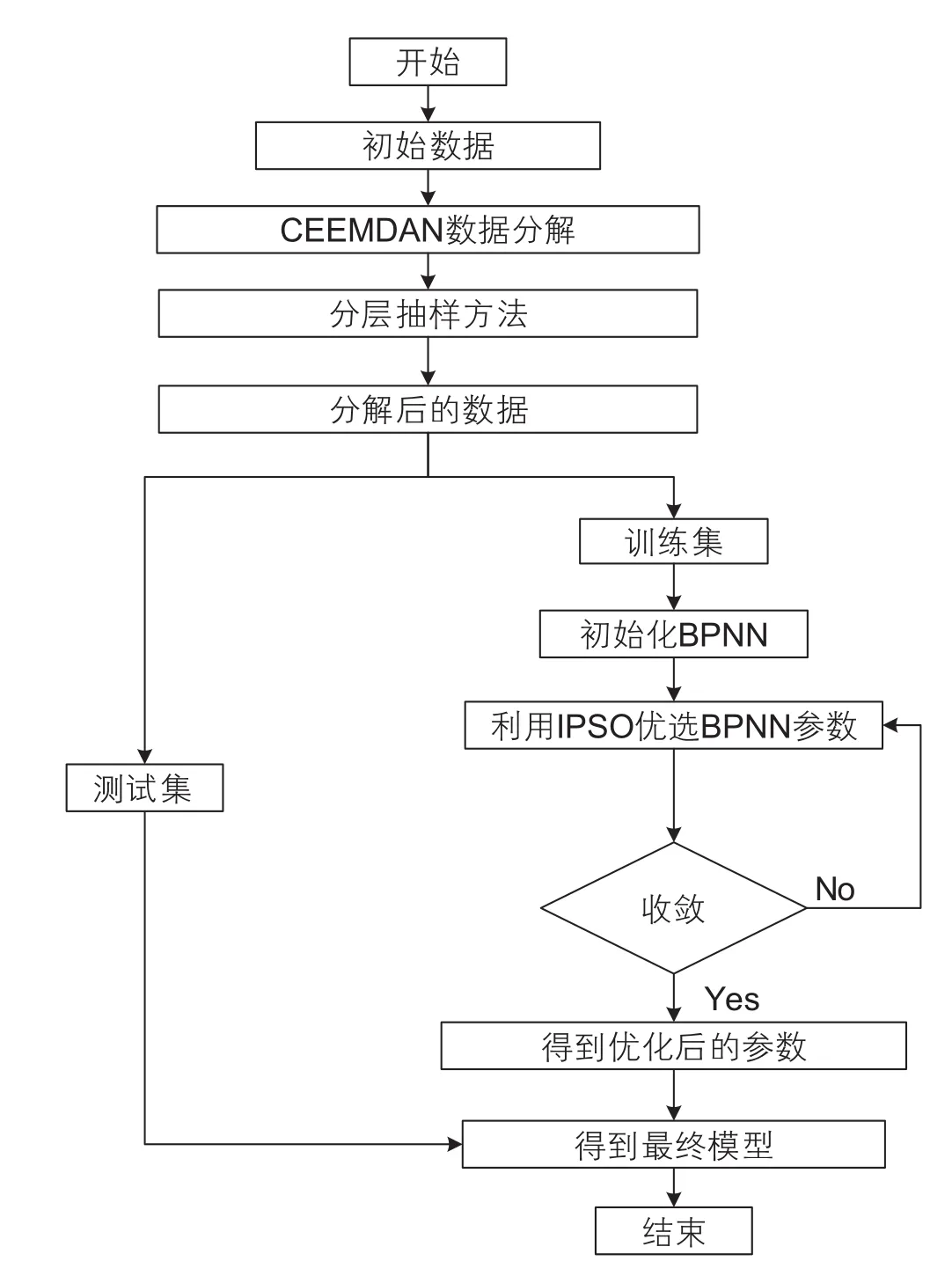
图7 CEEMDAN-IPSO-BPNN混合预测模型的流程图Fig. 7 Flow chart of CEEMDAN-IPSO-BPNN

3.2 与常规机器学习方法对比

将建立的混合预测模型CEEMDAN-IPSO-BPNN与GA-BPNN、PSO-BPNN、IPSO-BPNN、EMDIPSO-BPNN和EEMD-IPSO-BPNN 等5个模型展开预测性能对比，评价混合模型的预测性能。对3条管道的10个指标分别取平均值得到表5和图8，为了全面评价所提出混合模型的预测性能，开展了对比研究。

(1)通过GA-BPNN与PSO-BPNN的预测结果对比发现，PSO-BPNN的预测性能优于GA-BPNN，证明PSO对于预测性能的提高优于GA，相比主流优化算法，PSO对于预测性能的提高幅度较大。

(2)通过PSO-BPNN与IPSO-BPNN的预测结果对比发现，IPSO-BPNN的预测性能优于PSO-BPNN，证明改进粒子群算法在一定程度上提高了粒子群算法的性能，有效解决了优化算法容易出现局部最优解的问题。

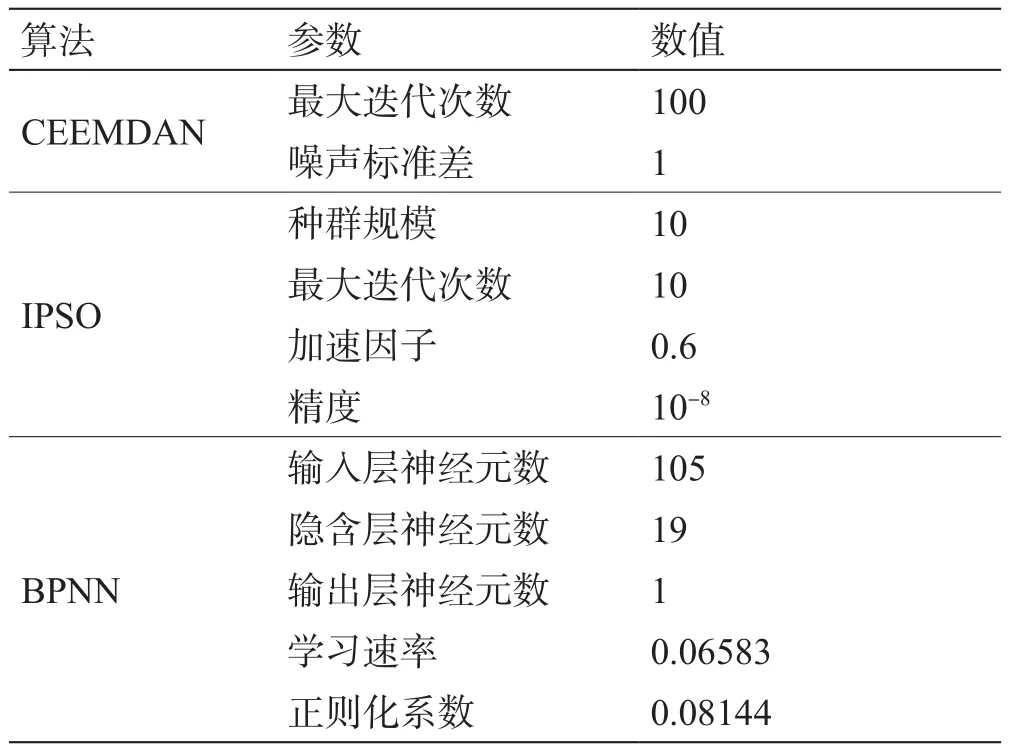
表3 实验参数值Table 3 Experimental parameters

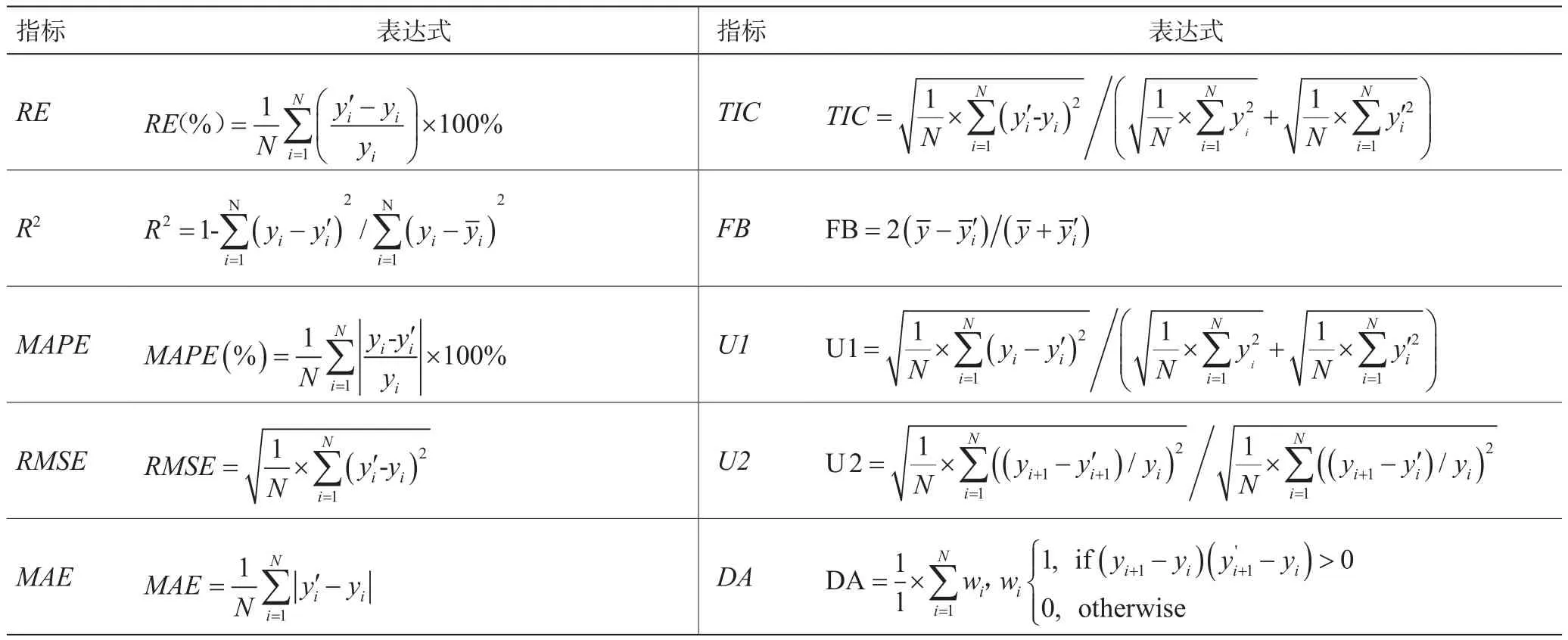
表4 模型预测性能评价的十个主流指标Table 4 Ten mainstream indicators for performance evaluation

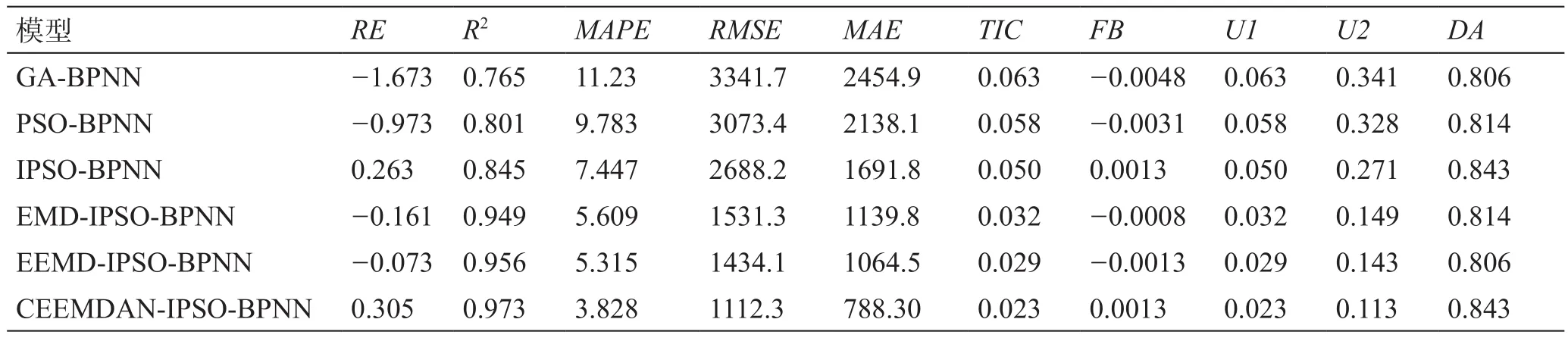
表5 3条管道上十个评价指标的平均值Table 5 Average values of ten evaluation indicators for the 3 pipelines

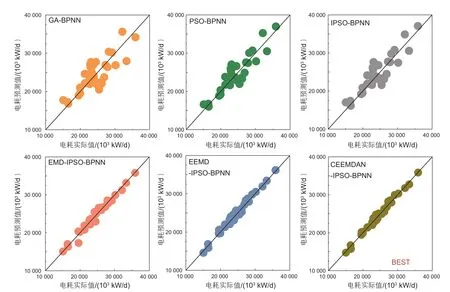
图8 建立的模型和对比模型的预测值Fig. 8 Predicted values of the proposed model and the comparison models

(3)通过IPSO-BPNN与EMD-IPSO-BPNN、EEMD-IPSO-BPNN和CEEMDAN-IPSO-BPNN预测结果对比发现，IPSO-BPNN预测效果相对最差，证明分解算法能够在一定程度上提高模型的预测性能。

(4)通过CEEMDAN-IPSO-BPNN与EMD-IPSOBPNN和EEMD-IPSO-BPNN预测结果展开对比发现，相比EMD和EEMD数据分解技术，CEEMDAN具有更好的分解效果，能够深入地捕获数据特征，提高模型预测结果。

因此，通过与5个机器学习模型的对比可知，建立的混合模型CEEMDAN-IPSO-BPNN具有最好的预测性能。

3.3 与SPS能耗预测软件对比

SPS是款成熟的瞬态水力模拟软件，能够模拟单一流体、批次流体和单相混合流体在管道中的输送过程。利用软件内置的管道、泵、压缩机、阀和控制器等，SPS能建立对应的数学模型，通过计算流量、压力、密度、温度和其它一些沿线随时间变化的参数来开展仿真研究。在油气储运领域，SPS软件使用广泛，主要功能包括停输再启动分析、管输能耗分析、泵和压缩机操作计划分析、水击泄压系统设计、批次计划、不同操作方案和不同设计的经济性分析等。

为保证预测结果具有可对比性，本研究以上文提到的管道A、B和C为例，运用SPS软件分别建立管输能耗预测模型。将预测结果与CEEMDAN-IPSO-BPNN的预测结果进行对比，深入评价CEEMDAN-IPSO-BPNN模型的预测性能。

首先建立站间管道系统模型，通过计算泵功率得到每天耗电量，模型采用设备Pump来模拟中间站的输油泵，采用General Pipe来模拟站间管道，管道输送介质采用出站掺混后的原油，泵的特性曲线、管道内径、管线长度以及掺混原油特性等数据通过现场获取。模型以进口控制压力、出口控制流量作为边界条件，计算泵机组每天耗电量。以管道A为例，图9为建立的SPS能耗预测简易流程，预测得到的部分结果如表6所示。对3条管道模拟得到的10个指标取平均值得到统计表7，图11为CEEMDAN-IPSO-BPNN与SPS预测结果相对误差绝对值的箱型图。

从结果上来看，SPS模拟得到的MAPE为10.72%，对造成现有误差的原因进行了思考，主要包括：(1)管道服役时间长，管道内壁产生磨损，粗糙度难以估计，与设计规范的推荐值有差别；(2)管道输送介质含蜡量较高，管道在长时间运行过程中会积蜡，并且管道的清管效果未知，影响了管道的实际水力半径；(3)站内管线复杂，模拟中只能粗略考虑站内的摩阻损失，直接影响了模拟数据的精确度；(4)总传热系数难以准确确定；(5)采集传感器的精度不准；(6)泵的实际运行特性跟厂家提供的特性曲线有偏差；(7)现场数据为一天的平均值或累计值，而不同时刻的数据存在波动性，仿真数据是根据一天的累计输量和平均压力稳态模拟所得到的，这与真实情况存在差别。

图9 基于管道A建立的SPS能耗预测流程Fig. 9 The SPS energy consumption prediction process based on pipeline A

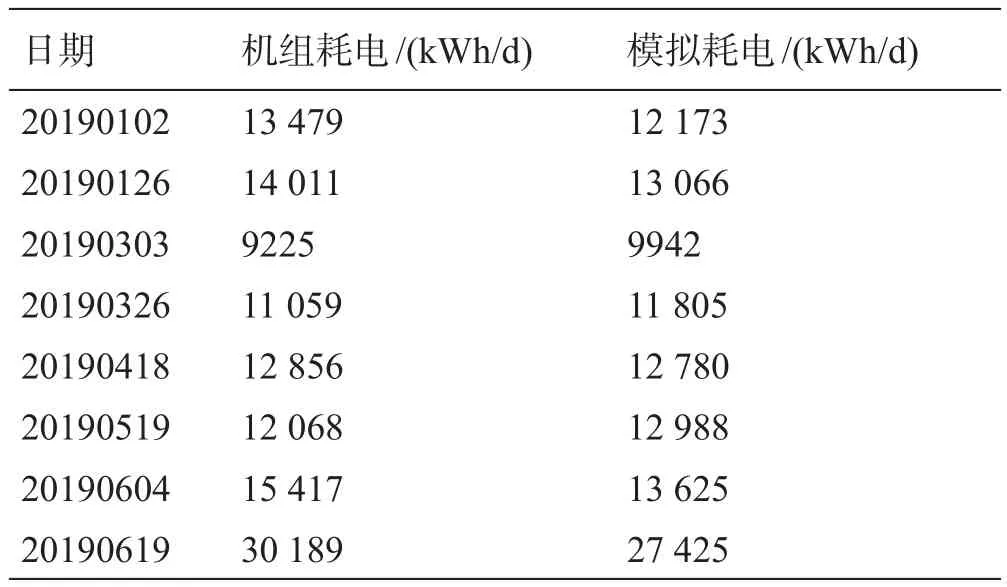
表6 基于管道A的部分预测值Table 6 Partial predicted value based on pipeline A

通过表7和图10分析可得，针对相同数据集，CEEMDAN-IPSO-BPNN相较于主流商业软件SPS拥有更好的预测性能。表明机器学习预测效果对于数据的依赖性要弱于SPS软件，运用SPS展开预测，若想取得理想的预测效果，需要详细的参数信息，在实际生产运行中部分参数较难获取。而机器学习能通过数据分解技术和非线性映射功提高模型的预测性能，也间接表明了基于数据驱动的机器学习方法在油气储运行业的优势和潜力。

表7 建立的模型预测值和SPS能耗模块预测值的对比Table 7 Comparison of the predicted values between the proposed model and the SPS energy consumption module

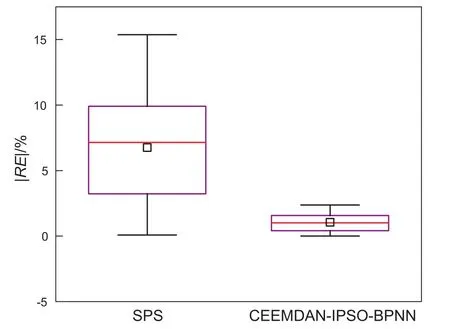
图10 混合模型与SPS预测相对误差绝对值箱型图Fig. 10 Box plot for the absolute value of the relative error between the hybrid model and SPS

4 结论

采用分层抽样方法对初始数据进行划分，避免出现简单随机抽样遗漏某些特性的问题，保证预测结果的客观性和可靠性。提出了基于反向传播神经网络的改进粒子群优化算法，提高了粒子群的搜索能力、避免了局部最优解。将自适应噪声完整集成经验模态分解技术应用到油气管道领域，与其他分解技术相比，该分解技术能够高效消除预测过程中的冗余噪声，捕捉原始数据集的主要特征。在此基础上，建立的混合预测模型综合了数据分解技术和优化算法的优势，对比5类主流机器学习方法和管输能耗预测软件SPS，建立的能耗预测模型平均绝对百分误差降低7.402%、5.955%、3.619%、1.781%、1.487%和6.887%，拥有较高的预测精度和较强的泛化能力，能有效指导能耗目标设定、调度优化和机组组合。提出的预测方法以机器学习为基础，解决了传统物理数学建模复杂等缺点，关注输入和输出参数的映射关系，在实际管道甚至是更加复杂的管道系统中也有一定的适用性。