分数阶对流扩散方程在大气污染中的应用浅析

刘桃花，尹修草

(湖南科技大学 数学与计算科学学院，湖南 湘潭，411201)

随着经济的快速发展和人类活动的增强，大气污染问题尤其是PM2.5污染问题日益严重，因此，准确预测PM2.5浓度对控制和治理PM2.5以及改善社会民生都具有非常重要的意义。目前，国际上主要通过大气环境定点监测方式获取各城市PM2.5的污染状况，运用多元线性回归统计方法、统计空间插值方法、神经网络方法等对PM2.5的浓度进行预测[1-6]。

XIE等[7]在研究广州市空气中PM2.5的扩散情况时，讨论了一类带Dirichelet边界条件的分数阶对流扩散方程，给出了数值方法及其应用。分数阶对流扩散方程用于模拟物理、生物、经济上的许多问题[8-10]。带分数阶边界条件的这类方程更适合实际问题的应用[11-15]，据此，对带有分数阶边界条件的分数阶对流扩散方程进行了数值研究，建立了隐性差分格式，然后分析了该方法的解的相容性、存在唯一性、稳定性以及收敛性，并探讨了该方法在长株潭地区大气污染中的应用。考虑污染物的分布情况及风速、温度、湿度等因素，建立长株潭地区PM2.5的扩散方程，对污染物的浓度进行预测，从而对该地区PM2.5的浓度进行预测。

考虑如下一类带有分数阶边界条件的分数阶对流扩散方程：

(1)

分数阶初边值条件为

(2)

u(x，0)=q(x)，0≤x≤R

(3)

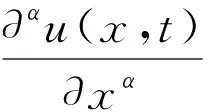
(4)

其中：Γ(·)为Gamma函数。

1 差分格式的建立

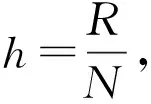
移位的Grünwald-Letnikov分数阶算子定义为

(5)

标准的Grünwald-Letnikov分数阶算子定义为

(6)

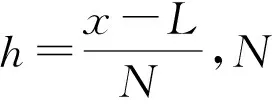
(7)

并且Grünwald系数满足如下引理。

引理1[16]假设α为正实数且整数n≥1，有

采用移位的Grünwald-Letnikov分数阶算子对方程中Riemann-Liouville分数阶导数进行离散，采用标准的Grünwald-Letnikov分数阶算子对分数阶边界条件中Riemann-Liouville分数阶导数进行离散，得到：

利用向后Euler差分方法，定义一阶时间和空间导数：

得到方程式(1)～(3)在点(xi，tm)处的隐性差分格式为

(8)

(9)

(10)

(11)

(12)

由方程(11)～(12)可知，建立的隐性差分格式是相容的。

2 隐性差分格式的理论分析

上面已经建立了方程(1)～(3)的隐性差分格式，下面讨论该格式的解的存在唯一性，稳定性以及收敛性。将方程(8)～(10)整理为

(13)

(14)

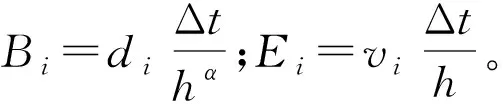
(15)

其中：

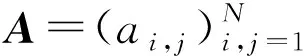
(16)

定理1如果β>0，方程(1)～(3)的隐性差分格式(8)～(10)的解存在且唯一的。

证明假设ri是第i行除了对角线元素ai，i之外所有元素绝对值之和，根据引理1，则有

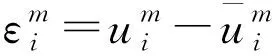
(17)

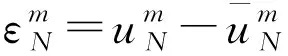
(18)

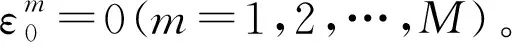
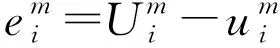
(19)

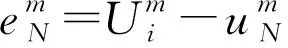
(20)

定理2若β>0，则方程(1)～(3)的差分格式(8)～(10)是无条件稳定的。

由引理1得

(21)

结合上面的不等式，由方程(20)可得

(22)

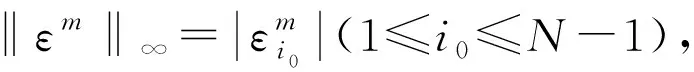
重复利用不等式(22)m-1次，则有

‖εm‖∞<‖ε0‖∞，1≤m≤M。

综上，方程(1)～(3)的差分格式(8)～(10)是无条件稳定的。

定理3若β>0，则存在不依赖于h和Δt的非负常数C，使得

(23)

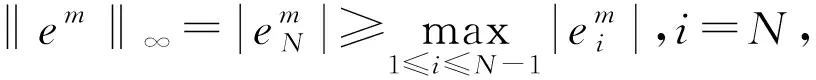
(24)

由Gamma函数的Stirling公式[17]，则有

(25)

结合方程(24)和(25)，则有

(26)

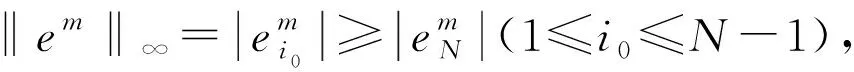
(27)

重复利用不等式(27)共m-1次，有

‖em‖∞≤(m-1)ΔtC2(Δt+h)。

又因为(m-1)Δt≤T，所以，存在一个常数C=C2T，使得

‖em‖∞≤C(Δt+h)

(28)

即存在不依赖于h和Δt的非负常数C，‖em‖∞≤C(Δt+h)，所以，此格式收敛。

3 分数阶扩散方程在长株潭地区大气污染中的应用探讨

本文中t表示扩散时间，x表示扩散距离；d(x)≥0，v(x)≥0，k(x)≥0，分别表示x轴方向的扩散系数(m2/s)、风速(m/s)和衰减系数(s-1)；f(x，t)表示点x在t时刻污染物的排放量；u(x，t)为污染物的质量浓度(μg/m3)。首先，根据长株潭地区的风速情况，估计v(x)的值。根据斐克定律，求出扩散系数d(x)。若PM2.5在不治理的情况下很难自动消失，则可以考虑k(x)=0。近几年来，国家致力于生态文明建设，空气质量明显好转。可以通过这几年的PM2.5估计出k(x)。根据检测数据，一般使用实测法计算，只需要查找某些数据，或者通过调查实测等估算污染物的排放量。其次，可以采用化学质量平衡CMB受体模型，通过分析污染源和受体样品中的化学成分来评价不同类型的污染源对环境污染物质浓度的贡献。其中，NKCMB 1.0是南开大学国家环境保护城市空气颗粒物污染防治重点实验室基于此模型开发的一个工具软件，使用此软件，可以得到长株潭地区的污染源类型和化学成分，然后，使用最小二乘法计算出各类污染源的贡献值，从而得出污染物的浓度。根据PM2.5的浓度变化评估治理效果等。

4 结论

本文考虑了一个带有分数阶边界条件的分数阶对流扩散方程，给出了一个隐性差分格式，证明该格式的解的存在唯一性，稳定性以及收敛性。结合该模型的实际背景，探讨了该分数阶对流扩散方程在长株潭地区大气污染中的应用。