基于双精英蚁群算法的配电网故障区段定位
陶维青, 肖松庆, 李 林, 曹 军
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.科大智能电气技术有限公司,安徽 合肥 230088)
0 引 言
分布式电源(distributed generator, DG)并网[1]使得配电网故障特性发生改变,基于传统故障信号的诊断方法[2]可靠性降低,而坚强智能电网的发展使得配电自动化[3-4]程度和覆盖率大大提高,中高压配网普遍安装了故障指示设备(fault indicating device, FID),如馈线终端单元(feeder terminal unit, FTU)[5]、开闭所终端单元(distribution terminal unit, DTU)、故障指示器等,提高了故障定位、隔离和供电恢复可靠性。故障定位方法一般分为直接法和间接法。直接法如典型的矩阵法虽然计算量小、运算速度快,但定位精度不高、容错性低。间接法包括各种智能优化算法,文献[6]基于遗传算法将传统行波测距方法中的预设波速替代为最优波速从而优化定位结果,但实际波速与优化波速相差较大时仍会降低定位精度;文献[7]结合模糊推理与模拟退火算法改进了传统遗传算法的评价函数和遗传机制,提高了定位的准确性;文献[8]提出一种基于分层结构模型和智能校验算法的定位方法,并对定位结果进行反馈校验,具有较好的容错性和稳定性;文献[9]提出对配电线路上的故障指示器状态采用二进制编码,通过人工鱼群算法进行故障诊断,但其仿真结果仍存在不少故障漏报的情况;文献[10]针对含DG的配电网提出一种基于故障电流的免疫算法,通过计算抗体的匹配程度和浓度来评价个体适应度,具有良好的收敛特性;文献[11]基于树状图搜索算法,利用FID信息、电话投诉信息建立网络树状图进行故障搜索,通过D-S证据理论融合故障信息提高了定位的准确性。
蚁群优化算法(ant colony optimization, ACO)是一种源于蚂蚁觅食行为的仿生智能算法,其基本模型最早由意大利学者Dorigo于1991年提出,并成功应用于解决著名的旅行商问题(travelling salesman problem, TSP)。精英蚂蚁系统是对基本蚁群算法的优化和改进,并在TSP问题中表现出更加优越的性能。文献[12]基于蚁群算法自适应动态修改信息素浓度,但尚未考虑DG接入配网的影响,只适用于单电源网络;文献[13]利用蚁群算法进行全局搜索,模拟退火算法进行局部优化,提高了定位精度,但仿真结果显示定位速度尚未得到明显改善;文献[14]基于FTU上传信息对多电源配网系统进行区段定位仿真,提高了定位精度,但没有提出FTU上传信息缺失和畸变情况的解决办法。
本文利用配电网各个节点FID的故障指示信息,将故障定位问题转化为TSP问题,采用蚁群优化算法中的双精英蚂蚁策略动态更新信息素浓度,建立适于含DG网络的开关函数和目标函数迭代寻优选出故障路径。对于多分支的配网可以划分为多个子区域进行分段故障诊断从而提高搜索速度。对FID上传信息缺失或畸变的情况提出了信息修复处理方法,最后仿真验证了定位的准确性、快速性和高容错性。
1 精英蚁群算法基本原理
1.1 蚁群算法
蚂蚁在觅食过程中会在路径上释放特殊的信息素来寻找路径,路径越短,信息素浓度越大。当蚂蚁碰到未走过的路口时会随机选择一条路径,而当碰到有蚂蚁走过的路口时,会选择信息素浓度大的路径,从而使最短路径上的信息素浓度越来越大,而其他路径上的信息素浓度会随着时间的流逝越来越低,最终找到最优觅食路径。
蚁群算法最初用于解决TSP问题。假定t时刻路径(i,j)上的信息素为τij,蚂蚁总量为m,各条路径上的信息素量决定了蚂蚁运动方向,定义pijk(t)为t时刻蚂蚁k从节点(i,j)转移到节点j的概率,由各条路径上的信息素和启发信息决定,计算公式如下:
(1)
其中,Ck为第k只蚂蚁即将选取的城市集合;Rk为第k只蚂蚁在当次循环中所走的路径区段集合;s为城市节点;ηij(t)=1/dij为蚂蚁从城市i转移到城市j的期望函数,dij为2个相邻城市之间的距离;α为信息启发式因子,表示蚂蚁觅食过程中积累的信息素对路径选取的影响程度;β为期望启发式因子,表示期望函数在路径转移中的作用程度。t+n时刻(i,j)路径上的信息素更新规则如下:
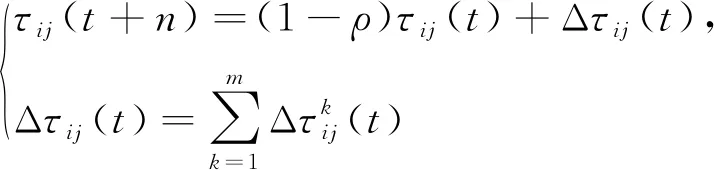
(2)
其中,ρ为信息素挥发系数;Δτij(t)为蚁群在路径(i,j)上留下的总的信息素增量。第k只蚂蚁经过路径(i,j)留下的信息素增量采用如下蚁周模型:
(3)
其中,Q为信息素强度;Lk为路径Rk的总长度。
1.2 精英蚂蚁策略
精英蚂蚁指的是蚁群算法迭代到当前次数为止,k只蚂蚁中所选路径最优的那一只蚂蚁。精英蚂蚁策略指的是对精英蚂蚁搜索到的路径上的信息素进行额外增强,利用当前最优路径代替每只蚂蚁各自所走的路径,从而达到优化算法收敛速度的目的。对(3)式进行改进得到(4)式,形成精英蚁群优化算法。
(4)
其中,Rbest为到当前循环次数为止k只蚂蚁中精英蚂蚁所走过的最优路径区段集合;Lbest为最优路径长度。
2 双精英蚁群算法用于故障区段定位
2.1 蚁群算法定位模型
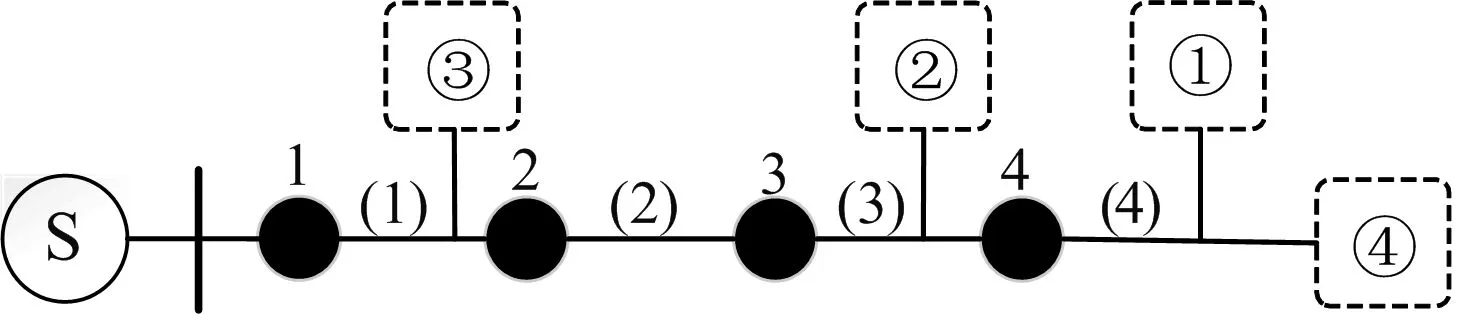
将蚁群算法应用于配电网的故障定位,就是要将网络节点之间各个区段状态的选择转换为TSP问题的最优路径选取,每一个安装了FID的节点相当于TSP问题中的不同城市,相邻区段之间有故障和非故障2个状态,相当于有2条路径约定故障状态为1,非故障为0,如图1所示,1~7为各个FID编号,a、b、c、d、e为各个区段编号。

图1 蚁群算法定位模型
蚁群会根据0、1路径上不同信息素浓度大小选择相应的路径,经过信息素浓度不断更新,最终会形成一条各个区段不同状态的集合,这个集合就是最优解,集合中为1的元素对应的区段号就是故障区段。
在TSP问题中蚁群算法的结果就是搜索到最短路径,目标函数即为所走各段路径长度的标量和,总长度最小时目标函数达到最优。在配电网故障定位问题中,区段的0和1状态没有大小关系区别,并不对应于传统蚁群算法解决TSP问题中相邻城市间的距离大小。因此需要对算法进行改进,建立适于配电网络故障诊断的目标函数和开关函数模型。
2.2 双精英蚂蚁策略
精英蚂蚁优化算法加快了收敛速度,但是每次迭代的最优解存在较大偶然性,极可能陷入局部最优,导致得出伪故障点。因此本文采用双精英蚂蚁优化算法,即在精英蚂蚁之外再增加一只蚂蚁,其所选取的路径长度次优,2条路径上的信息素浓度同步更新,相互制约,从而扩大了搜索范围,避免了过早陷入局部最优。
信息素浓度更新规则即在(4)式的基础上乘以约束系数ε,得到信息素增量如下:
(5)
其中,ε=1+2(Lb2-Lb1)/(Lb1+Lb2);Rb1、Rb2分别为2只精英蚂蚁所选路径区段集合;Rb1为最优路径集合,Rb2为次优路径集合;Lb1、Lb2分别为2条路径的长度,且Lb1 蚁群算法的相关参数选取范围见表1所列。 表1 蚁群算法相关参数 因为蚂蚁选择路径0和路径1的期望程度是未知的,所以约定2条路径被选择的期望程度一致,取均值为1,即β为1,同时α取1具有较好的收敛特性,也减小了(1)式的计算量,提高了算法的计算速度。参数Q取值如下: (6) 其中,Nc为迭代次数。Q随着Nc的增大而增大从而提高优化速度,一般计算迭代不超过15次就出现全局最优解,故设定Nc大于15时系数Q不再变化。同理参数ρ的取值如下: (7) 本文取最大迭代次数Ncmax为30次,即当Nc=30时停止迭代,蚁群数目m=4。 含DG的配电网络发生短路故障时, DG相对于主电源可能提供反向短路电流,从而造成FID状态具有方向性,因此对FID节点上开关s的状态上传值Is进行如下编码,即 (8) (9) 其中,ku、kd分别为开关s上游接入主电源和下游接入DG的状态,接入为1,未接入为0;Sd、Su分别为开关s至上游主电源各区段及下游DG各区段的状态,故障为1,非故障为0;P、Q分别为从开关s至上游主电源及下游DG的区段个数。(9)式求和运算取0-1编码的求和运算,即 “或”运算。 发生多重故障时,可能存在同一个节点既有流过主电源提供的故障电流,又有DG提供的反向故障电流,由于DG容量远小于主电源容量,因此约定此时电流方向由主电源决定。对于图1所示网络,当故障发生在f1处时,节点1、2流入正向故障电流,节点3、6、7流入反向故障电流,节点4、5无故障电流,此时FID信息上传值为[1 1 -1 0 0 -1 -1],当故障发生在f2时, FID信息上传值为[1 1 1 1 0 -1 -1]。当f1、f2同时发生故障时,节点3既流过正向故障电流又流过DG提供的反向故障电流,取其状态为1, FID信息上传值为[1 1 1 1 0 -1 -1]。 可见故障一般出现在支路末端节点状态为1的区段。而当发生有故障路径重复时的多重故障时,只能检测到最末端的故障,与文献[15]利用邻接表和关系表得到的定位结果一致,此时需要将故障切除后再次诊断。 建立合适的目标函数是改进蚁群算法的核心。配电网故障区间诊断的原则是使得各馈线段FID状态信息的实际值和上传值最小,本文根据实际配电网在一条故障路径上多以单点故障为主,得到目标函数如下: (10) 其中,σ为故障权重因子;Sb为目标函数解集,由(9)式知(Sd,Su)为Sb的子集;N为蚁群所走路径的区段数。 当某个FID开关状态上传值与期望值不相等时,(10)式求和运算内第1项值为1,此时若权重因子σ取1则易发生混淆,本文取σ为0.7。 实际配电网络结构相对复杂,具有多个分支,实际开环运行的配电网络为含双DG的25节点系统,1~25为各个FID编号,(1)~(17)为各个区段编号,如图2所示。蚁群算法的复杂度随着节点个数的增多而增大,使得算法的效率降低,从而需要进行网络分区以简化计算。 图2 含双DG配电网络 选取图2中不含DG且节点较多的支路为主支路,即由FID 1~8组成的支路。将含DG的支路分别划分为区域①和区域②。其次由于节点9、10和节点11~15位于同一主支路连接点且不含DG,故划分为同一区域③,同时由于区域③的节点距离DG较远,实际情况下考虑到DG的弱馈作用,DG对区域③节点状态的影响较小可以忽略不计。 此外由于节点5~8均位于主电源和分布式电源的下游,发生短路时电流方向均为正向,节点状态不受DG影响,故划分为区域④。简化后的网络如图3所示。 图3 简化网络 各个区域之间的节点状态互不影响,但各个区域内部发生故障与否会对主支路节点状态产生影响。为了提高计算效率,实际配网中每个区域对应于一台独立计算机,各计算机同时对各区域节点FID上传的故障信息进行故障搜索,完成局部区段定位,此时每个分区可以等效为单个节点,再连同主支路4个节点的故障信息在同一主站计算机进行故障搜索,完成全局区段定位。 网络分区处理将25节点系统转化为8节点系统,使得可行解个数大大降低,从而提高了算法的运算速度与定位速度。 信息缺失相当于FID状态信息数量减少,使系统维数减少,定位结果准确率降低。信息畸变使得FID状态信息失效,可能导致定位失误,产生伪故障点。 为了尽量提高算法的容错性,总结文献[13]对信息缺失时的处理办法,本文对某一开关s的缺失状态信息Is作如下修正: (11) 其中,Isu、Isd分别为与开关s相邻的上下游FID信息上传值。若与开关s下游只有一个FID,则Isd的取值即为此下游FID信息值;若开关s下游有多个相邻FID,则Isd取值如下: (12) 即有1取1,无1时有-1取-1,全0取0。当s上下游FID开关状态不一致时可能导致修正失误,此时会将信息缺失转化为信息畸变。 当某支路发生短路故障且有节点信息畸变时,根据含DG复杂配网的拓扑结构有:当支路包含2个电源且其中一个为主电源时,则该支路节点FID上传值不为0;当支路只包含主电源或支路节点位于主电源和分布式电源下游时,这些节点的FID上传值不为-1;当支路上某个上游节点所属的子节点上传的信息都为1时,则该上游节点FID上传值不为-1。 不符合上述规则的畸变节点保持其畸变状态不变。 双精英ACO算法流程如图4所示,取Ncmax=30,m=4,在CPU型号为酷睿i5、主频2.85 GHz的个人计算机Matlab环境下,分别对FID信息上传值不同状态下的情况进行仿真。 图4 算法流程 FID上传值无信息缺失和畸变情况如下: (1) 设置区段(12)发生单点故障。 (2) 设置区段(12)、(15)发生双重故障。 对上述2种情况分别进行仿真,结果见表2所列。算法运行时各代全局目标函数值曲线和CPU时耗曲线如图5所示。 表2 上传信息正常时仿真结果 表2中未标出的区域FID上传值均为0。由表2可知,当某一分区内出现单点故障时,最优目标函数值为0.7。图5a显示目标函数首次出现最优值时,发生单点故障和双重故障的迭代次数分别为4、5次,目标函数值分别为0.7、1.4,均达到全局最优。图5b显示达到最优时CPU时耗分别为3.5、5.6 ms,时耗随着迭代次数增多而增大,双重故障时耗略大于单重故障时耗。 (a) 目标函数值 在设置同一双重故障条件下采用传统ACO算法和双精英ACO算法分别进行200次仿真,每次仿真均进行60次迭代运算,得到各算法运行时CPU平均时耗以及目标函数值首次达到最优时的迭代次数,见表3所列。 表3 不同ACO算法结果对比 由表3可知,在同一故障条件下双精英蚁群算法有着更优越的定位速度和收敛特性,能够在较少的算法迭代次数下进行快速定位。 将其与文献[16]中的遗传算法(genetic algorithm,GA)和人类进化算法(human evolutionary algorithm,HEA)分别比较,结果见表4所列,依旧显示出优越的收敛性能和定位速度。 表4 算法比较结果 (1) 设置区段(14)、(16) 发生双重故障FID4和FID17信息缺失,上传值分别记为x和y时,根据上文的信息缺失处理方法将信息补全后有x=0,y=1。 (2) 设置区段(11)、(12)、(17)发生三重故障, 正常情况下FID3、 FID19和FID21上传值分别为1、0、1,假定他们分别畸变为0、1、0,畸变信号用下划线标出。根据信息畸变修正方法将FID3和FID21的状态均修正为1,而FID19不符合上文的信息畸变修正规则,其状态保持不变。 定位结果见表5所列,表5中未标出的区域FID上传值为0。算法运行时各代全局目标函数值曲线和CPU时耗曲线如图6所示。 由表5可知,算法对于信息缺失和畸变的情况均定位准确。当发生信息缺失时,根据信息补全方法得到的主支路FID4信息补全值与期望值相反,同时主支路区域内无故障区域最优目标函数值为1,全局最优目标函数值为2.4,从而将信息缺失转变为信息畸变。当发生信息畸变时,由于区域② 内的FID19仍处于畸变状态,同时区域有单点故障,因此区域最优目标函数值为1.7,全局最优目标函数值为3.1。 表5 信息缺失和畸变时仿真结果 (a) 目标函数值 图6b显示在多重故障下,发生信息缺失和信息畸变时,目标函数首次达到全局最优时的迭代次数分别为5、6次。达到最优时CPU时耗分别为5.7、7.5 ms,时耗随着迭代次数增多而增大,三重故障时耗略大于双重故障时耗,2种情况下均能快速准确定位,同时显示算法良好的容错性。 本文利用双精英ACO算法对含DG复杂配网进行故障区段定位,通过动态调整信息素浓度及其他参数建立适于DG接入配网系统的开关函数和目标函数,将故障区段的定位问题转化为最优路径的求取问题。其次对复杂配网进行区域划分,先进行局部故障搜索,再转化为全局定位结果,降低了配网的复杂度,通过仿真与传统ACO及其他智能算法进行对比,优化了算法的收敛特性,同时提高了定位速度。 对于FID上传信息缺失和畸变情况,通过对含DG配网的拓扑分析总结了信息缺失修正方法,将部分信息缺失转化为信息畸变;其次针对配网结构提出了信息畸变的修正规则,并通过仿真分析了双精英ACO算法在不同故障情况下的速度特性和收敛特性,结果显示该算法具有优越的定位准确性、快速性以及良好的容错性。2.3 参数选取

2.4 开关函数和目标函数

3 网络分区处理

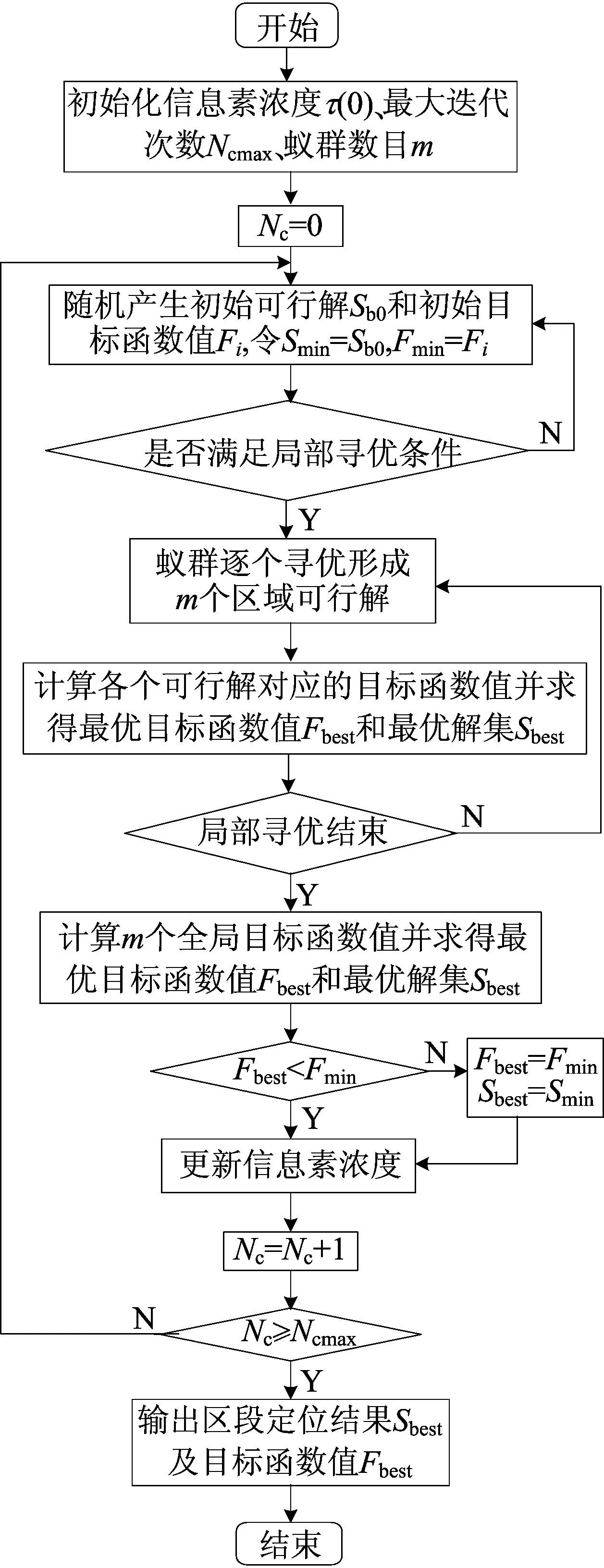
4 信息缺失和畸变处理
4.1 信息缺失修正
4.2 信息畸变修正
5 仿真验证
5.1 上传信息无缺失和畸变

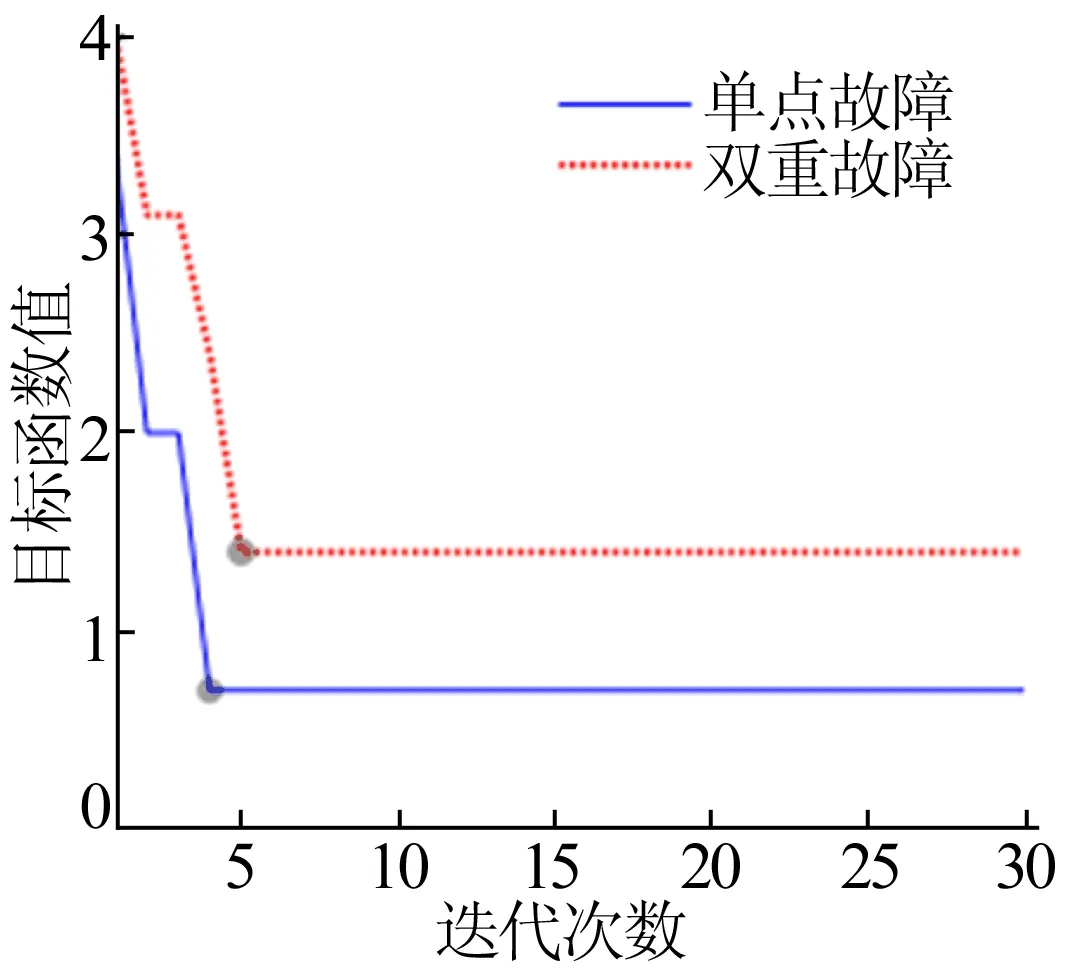


5.2 信息缺失和畸变

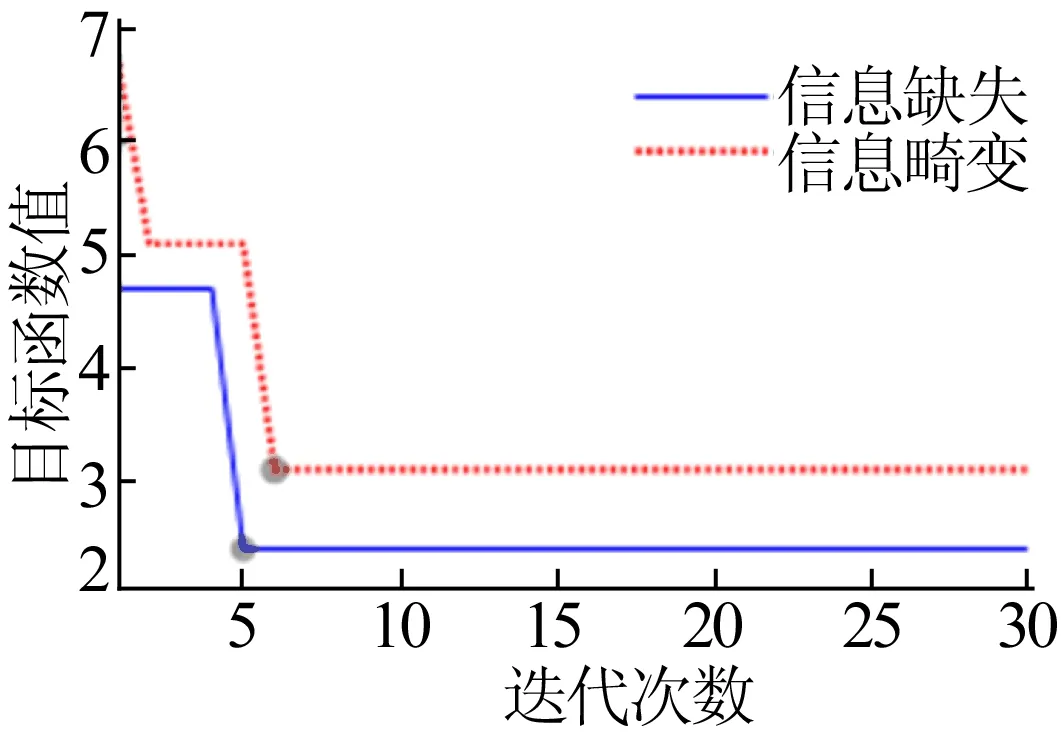
6 结 论

