复合材料构件成型模具型板改进设计

花蕾蕾，安鲁陵，赵一鸣，魏灵航

(1.南京航空航天大学 机电学院，江苏 南京 210016; 2.航空工业金城南京机电液压工程研究中心，江苏 南京 210016)

0 引言

近50年来，先进复合材料因其高强度、耐高温、抗疲劳等优点，在航空航天、机械工程、医疗、交通等行业得到了日益广泛的应用与发展。尤其是航空制造业，复合材料在飞机中的应用比例逐年提升，成为航空工业中主要发展和研究的对象[1-2]。

热压罐工艺依旧是目前航空企业在复合材料构件成型中主要使用的一种成型方法[3]。复合材料构件的温度场主要分为内部温度场和外部温度场。其中，构件与热压罐内空气的热对流为外部温度场，模具与构件之间、模具及构件本身的热传导则为内部温度场。成型模具与构件在罐内压力的作用下始终紧紧贴合，因此成型模具型板表面温度的均匀性对构件的温度场形成起到了不可忽视的作用。随着罐内空气的循环流动，根据对流换热的特点，复合材料构件温度场始终呈现随加热方向梯度变化趋势[4]，其中成型模具型板表面与构件之间的热传递对这一现象起到了主导作用。复合材料上温度梯度的存在，则会在成型过程中导致构件内部固化度不同步，形成残余应力，在最终脱模时释放，形成固化变形。固化变形不仅会影响构件成型精度，还会影响使用寿命甚至报废[5]。

目前国内外对于成型模具温度场的改进主要从工艺参数和成型模具入手，其中针对成型模具，大多通过模具支撑结构与模具结构改进。张铖等[6-7]提出风速、温度速率等工艺环境参数对于模具型面温差具有重要影响。林家冠等[8]通过对框架式模具温度分布的规律研究，设计了一种在支撑结构散热口附近安装风扇的方法，以达到加强底部气体流通的作用从而增强型板表面温度分布均匀性。傅承阳等[9]则通过有限元仿真，研究确定成型模具表面低温区域，设计了一种在低温区域安装加热器的方法以改善成型模具温度分布。张旭生等[10]通过改变模具支撑结构散热口的闭合改变底部气体流动风道，研究发现T型风道对于型板表面温度均匀性的提高效果最佳。

本文从模具结构出发，根据仿真结果确定模具型板表面低温区域，通过对模具型板变厚度设计，改善气体在流通中的热量损耗，以实现温度均匀地提高。

1 数值模拟分析

复合材料构件热压罐成型是一个多场耦合的复杂过程。对复合材料传热情况分析如下。

1)罐内空气与固体区域(模具和构件)之间通过气体流动以对流换热的方式传递热量。

2)由于脱模剂传导率低且厚度比较薄，因此可忽略其对传热的影响。本文仿真时假设成型模具与构件在固化中受压力作用，模具型板上表面与构件下表面紧密贴合，两者之间进行热传导。此外模具本身存在热传导。

3)复合材料构件内部树脂基固化放热，同时存在自身热传递。

在以上传热规律的基础上，对热压罐固化过程中成型模具温度场进行模拟仿真。

1.1 基本方程

根据连续介质假设，质量守恒、动量守恒和能量守恒3个基本方程的微分形式如下：

质量守恒方程：

(1)

动量守恒方程：

(2)

能量守恒方程：

-pdiv(U)+div(λ·grad(T))+Sh+φ

(3)

理想气体状态方程：

ρ=f(p·T)

(4)

式中：ρ为流体密度；U为流体速度；η为流体动力黏度；p为压力；Su、Sv、Sw为动量方程的广义源项；h与流体压强和流体温度相关；λ是导热系数；Sh为内热源；φ为耗散函数；T为温度。

对于固体区域，其能量方程为

(5)

式中：ρs为固体密度；cs为固体比热；Ts为固体温度；QT为内部热源项。

1.2 模型建立与网格划分

热压罐在航空领域常用于为复合材料构件成型时提供所需温度和压力。成型前需将预浸料、脱膜材料、透气毡等材料按序铺放于模具之上，进行密封处理，再在真空袋中入罐。一般固化过程将经过升温—加压—保温—降温—降压的过程，其中罐内热量主要通过空气的流动进行传递。

本文将热压罐工作内腔简化为圆柱体，成型模具为传统框架式模具，如图1所示。研究所用模具尺寸大小为1 500 mm×1 500 mm×400 mm，金属钢。热压罐工作内腔直径为2.5 m，长7 m。

图1 框架式成型模具结构

在FLUENT流体仿真之前，需要对简化后模型进行网格划分。本文所用模型为框架式模具，结构简单，可采用网格质量高、计算精度高的结构网格进行划分，得到近15×104结构网格。

1.3 流体流动模型和边界条件

将上一步所得热压罐及模具的网格文件导入FLUENT进行计算。本文使用的传热介质为空气，密度为1.237 kg·m-3，气体流速为1.5 m·s-1，动力黏度为1.79×10-5Pa·s。一般来说可通过对雷诺数Re判断流体流动模型。

(6)

由式(6)可知Re≥8 000～12 000，判断流体流动为湍流，FLUENT计算模型选择标准k-ε模型。

根据热压罐工作原理设定边界条件如下：

1)热压罐入口设为速度入口(velocity-inlet)，通过UDF(user defined function)编译固化温度曲线如图2所示[4]。

图2 简化工艺曲线

2)热压罐尾端采用压力出口(pressure-outflow)。

3)壁面设置为Wall。

1.4 模拟结果和分析

将仿真结果与文献[4]中的实验数据进行验证比对(图3)，两者误差在5%左右，验证了仿真的准确性。图4为升温结束时型板表面温度分布，此时最大温差为50.1 K，温度方差为166.27 K2，温度整体呈阶梯状分布趋势，其中在距迎风端80%的地方出现低温区域，占总面积的25%。

图3 实验数据曲线和仿真数据曲线对比

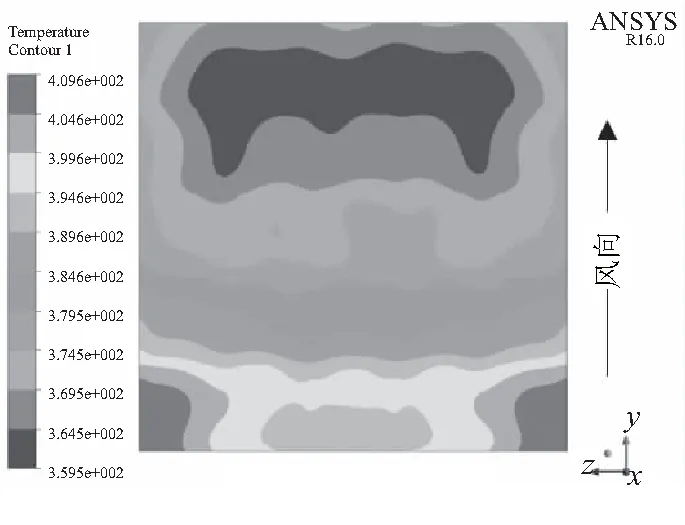
图4 T=7 200 s时型面表面温度分布

2 非等厚型板模具温度场模拟

导致上文型板表面出现阶梯状分布趋势主要原因为：一方面，流体在外掠过型板表面时，由于其黏性会在交界处形成边界层，而随着流体的流动方向动能逐渐耗损，边界层越来越厚，热阻随之变大[11-12]。另一方面，模具底部支撑结构在射流冲击换热时入风端处的隔板起到了阻碍作用，导致冲击强度随着气体的流向降低。因此可设计一种非等厚型板以适应型板表面不同热阻作用。

2.1 梯形非等厚度型板

根据图4可知高温区域出现在迎风端端口附近区域。因此设计4组梯形非等厚型板，从迎风端口处开始，分别至距迎风端400 mm、450 mm、500 mm和600 mm处。原框架式成型模具型板厚度为15 mm，此处对型板进行变厚度处理，将高温区域厚度调整为20 mm，其他区域降至10 mm。T=7 200 s时型板表面温度分布如图5所示。

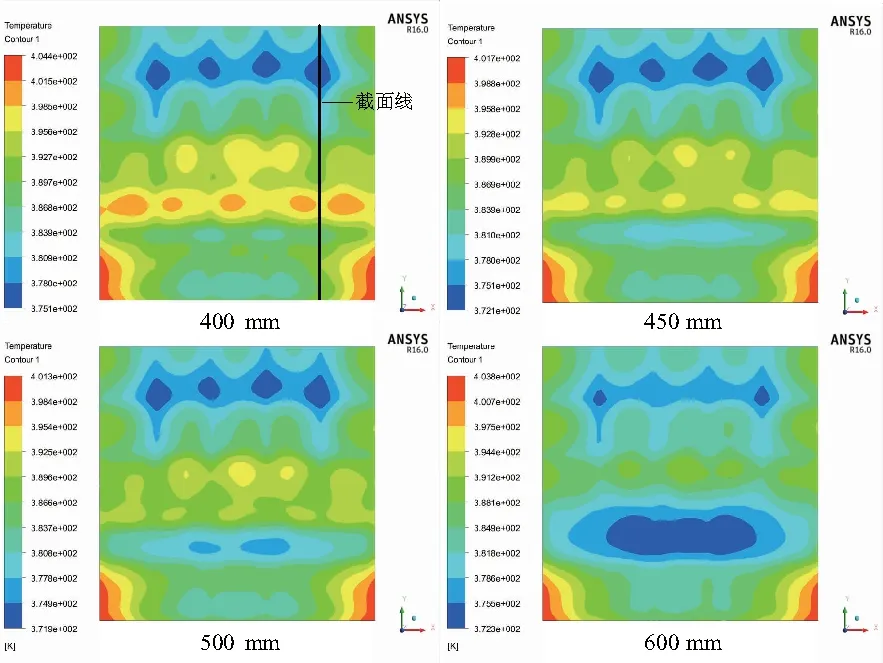
图5 T=7 200 s时梯形型板表面温度云图

由图6(a)可知，以上4种梯形型板在不同程度上对于型板表面温度均匀性均有所改善。其中距离迎风端500 mm时，最大温差为29.81 K，相较原始型板降低了40.51%，最大温度方差43.8 K2，降低了73.65%。如图5所示，所有型板表面在过渡区均出现温度起伏区域，其中400 mm和600 mm在厚度过渡区域更为明显，因此可通过对距离迎风端30%～33.3%处进行加厚处理。

根据图6(b)和表1可知，在厚度从20 mm～10 mm突变区域，型板表面出现最大温度起伏，其中最大温度起伏区域多出现于厚度突变交界处。随着距迎风端距离增大，突变区域距离迎风端越远，温度起伏区域也随之后移，且区域长度及温度差随之增大。此外由图6(b)可知梯形型板并未对低温区域位置产生影响，仍出现在距离迎风端115 mm左右。

图6 梯形型板表面温度曲线分析

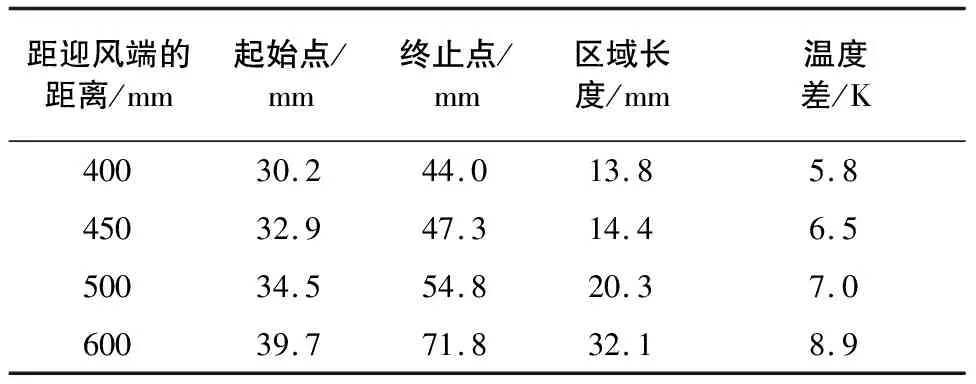
表1 不同距离温度起伏区域及温差

2.2 阶梯形非等厚度型板

由上节可知，梯形型板虽然在一定程度上有效地提高了型板表面温度均匀性，但在厚度突变区域都出现了明显的温度起伏区域。在此基础上，设计一种阶梯形型板，在高温区域将厚度采用逐渐递减的方式，将厚度从20 mm递减至10 mm并保持。同时，根据上节所产生的突变处温度起伏，将距迎风端距离增大，采用阶梯形变化趋势，取消厚度突变区域，使得高温区域后面区域更接近于原厚度，从而缓解突变改善均匀性。本文共设计6组实验，分别距离迎风端600 mm、700 mm、800 mm、900 mm、1 000 mm和1 100 mm。T=7 200 s时型板表面温度分布如图7所示，阶梯形型板表面温度曲线如图8所示。

图7 T=7 200 s时阶梯形型板表面温度云图

图8 阶梯形型板表面温度曲线分析

根据图7和图8可知，相较于梯形型板，阶梯形型板表面云图未出现明显的起伏现象。此外，根据图8(a)对比这6组数据，阶梯形型板对于温度均匀性改善起到了一定作用，其中当距离迎风端900 mm时，最大温差与温度方差都达到了最小值，即温度均匀性达到最佳状态。此时最大温差为32.78 K，相较于原始温差降低了34.56%，温度方差为32.26 K2，下降了70.25%。

2.3 连续变厚度型板

前两种变厚度方式均为对固定区域进行厚度变厚处理，本节中提出一种从迎风端开始处幂函数连续变厚度方式。本文采用s∝xn厚度变化函数，其中s为型板厚度，x为距迎风端距离，其中n取0.5～1。其型板表面温度分布与温度均匀性参数结果如图9和图10所示。

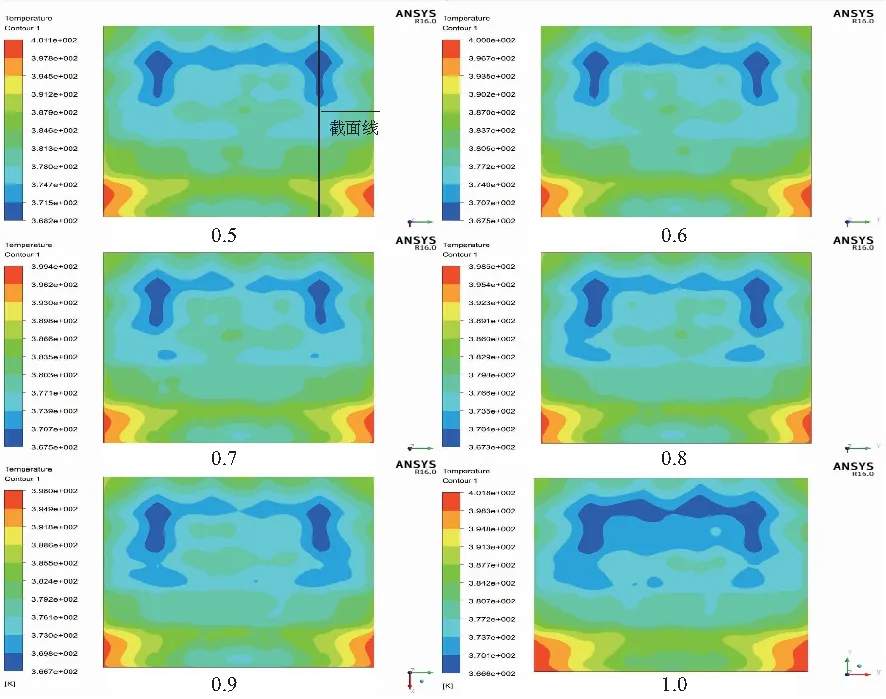
图9 连续变厚度型板表面温度分布

图10 连续变厚度型板表面温度曲线分析

根据图9和图10(a)可知，当n为0.8时，最大温差及温度方差达到最小，即型板表面温度均匀性最好，此时温度方差为25.98 K2。而随着n的增大或减小，温度方差也随之增大或减小。周光炯等[12]研究表明，温度边界层与速度边界层成正比相关，且δt∝x0.8。当n为0.8时，即s∝x0.8时，型板厚度变化规律与温度边界层厚度变化规律同步，因此型板表面温度均匀性达到最佳。

3 结语

本文利用FLUENT进行热压罐固化过程中温度场模拟。研究发现型板表面低温区域出现在距迎风端115 mm处，约占面积25%。为有效提高型板表面温度均匀性，本文提出一种对型板不同区域变厚度方法，分别对型板低温区域减厚和高温区域加厚。主要包括3种厚度方法：梯形、阶梯形、连续变厚度，通过有限元仿真对改善后型板分别进行模拟型板表面温度分布均匀性，分析得到以下结果：

1)梯形型板在突然变厚度区域存在明显的温度起伏现象，其中400 mm与600 mm尤为明显，因此可通过对距离迎风端30%～33.3%处进行加厚处理。

2)阶梯形型板未出现明显温度起伏现象，当距离迎风端900 mm区域加厚时，温度均匀性达到最佳状态，温度方差降低近70.25%。

3)连续变厚度型板采用s∝x0.8函数关系时，型板厚度变化规律与温度边界层厚度规律一致，此时温度均匀性最佳，结果表明此时温度方差降低了84.37%。