不确定条件下机场群系统均衡配流模型研究

盛 寅，陈 欣，毛 亿

(1.空中交通管理系统与技术国家重点实验室，南京210014；2.南京财经大学管理科学与工程学院，南京210023)

0 引 言

从世界范围来看，城市群内航空运输发展到一定阶段都纷纷由单机场模式向机场群模式转变，其典型特征是在城市群内部存在多个机场并共同服务于区域航空市场，国内如京津冀、长三角、珠三角等城市群的机场群系统已基本形成，并逐渐成为我国民航机场体系发展的一种重要模式.然而，世界主要大都市区机场资源利用不均衡，表现在核心城市机场的旅客过多，资源使用情况紧张，造成航班延误和机场服务质量下降；周边城市的旅客量少，机场设施闲置，资源得不到充分利用并出现亏损.

从航空客运组织过程来看，上述矛盾的根本原因在于航空客流在区域机场群系统内分布不均衡，导致系统在时空和功能上混沌无序，使区域航空需求与航空资源供给不能实现合理匹配.因而单纯的机场容量提升和航线补贴[1]方法对机场群系统资源利用不均衡的治理效果不理想.

学者尝试从旅客对机场的选择偏好角度入手探寻客流分布规律，从而优化客流分布.Yang 等[2]基于旅客出行效用提出Nested-Logit 机场选择模型，分别利用美国旧金山和上海的数据验证了方法的合理性.Luca等[3]建立随机效用离散选择模型用于研究出发机场的选择，随机效用综合考虑了费用，航班的频率，到机场的地面时间等因素.Hess[4]研究了在机场群选择时旅客的偏好，结果表明，旅客更偏向于选择大且近的机场.

然而，旅客出行不仅包含空中航线，还包含地面路径.在对地面交通模型研究方面：Yang 等[5]提出在动态交通网络中，基于线性整数规划的道路建模与选择方法，实现以一定的可靠性准时到达；Chen等[6]同时考虑道路的通行时间及可靠性，提出基于时刻匹配的混合遗传算法为个人道路选择提供指导；Zhang 等[7]在道路随机通行时间只有部分分布信息的前提下，提出近似的道路选择方法，并验证了方法的鲁棒性；徐爱庆等[8]从用户的偏好出发，以累积前景理论建立用户的效用，分析旅客出行特征.

上述研究成果缺乏对整个航空出行链的考察.从航空出行全过程来看，机场选择问题并不只是机场间的竞争问题，而是航空出行路径选择问题.地面交通研究中对空中交通的不确定性大、出行成本变动大等特征缺乏分析.

因此，本文综合考虑空中与地面交通，从旅客偏好角度出发，以出行时间、出行票价、机场服务水平为主要参考属性，研究客流在机场群系统中的分布规律，建立均衡配流模型，探索机场群客流分布规律.为提升机场利用率，降低旅客出行成本提供理论支撑.

1 配流问题建模

1.1 出行模型

假设G=(N,A)表示一个机场群交通网络，其中，N为节点集，表示机场、汽车站、火车站等交通枢纽，A为路段集，表示各枢纽间的路线.对于某一OD(Origin-Destination)对，设p(rs)为起点r与终点s之间所有路径的集合，机场群旅客出行时一般选择成本最小的一条路径p(p∈p(rs)).

机场群旅客出行成本不仅包括路径上的出行时间(简称路径时间)，还包括在机场停留时间及出行票价，记为

式中：η、D、H分别为路径时间、机场停留时间和出行票价；ω为旅客的时间价值.

旅客主要分为两类：商务型和休闲型.商务型旅客的时间价值较高，休闲型旅客的时间价值较低.本文基于上述因素分析机场群的客流分布规律.

1.2 路径时间

一般情况下，路径时间是旅客考虑的最重要因素.在机场群系统中，路径时间存在很大的不确定性.影响路径时间不确定性的原因主要分为两类：供给的不确定性和需求的不确定性.供给的不确定性指交通系统容量的变化，例如突发事故导致的地面交通拥堵，天气原因或军事活动导致的流量控制等；需求的不确定性是出行旅客数量的波动，例如节假日或重大事件期间旅客人数增加，淡季旅客人数减少等.因此，路径时间不仅应考虑平均值，还应考虑风险.

行程时间与人数相关时，路段时间ta采用BPR(Bureau of Public Road)函数计算，即

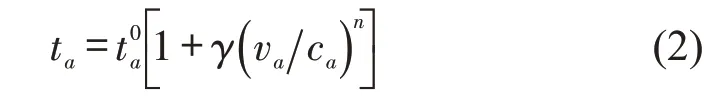
式中：、va、ca分别为路段a的自由流行程时间、流量、容量；γ、n为BPR函数的参数.

路段时间均值分为两类：一类与路段上总人数相关，如公交、出租车等地面交通，此时n＞0；另一类与人数无关，如高铁、航线等，此时n=0.

受交通供需影响，路段a的行程时间ta为随机变量，本文假设其服从正态分布，即

式中：、分别为行程时间ta的数学期望、方差.

对路径时间的不确定性有多种衡量方法，由于预算超出时间(Mean-Excess Travel Time，METT)将路径时间的均值与方差统一表示，故采用METT来综合评估路径时间成本.

定义1起点r与终点s之间的路径p在置信度α下的路径时间预算(Travel Time Budget，TTB)(α)为路径时间变量ξ的最小值，ξ满足实际路径时间不超过ξ的概率不小于α.表达式为

定义2METT为起点r与终点s之间的路径p在预先定义的置信度α下，超过相应路径时间预算的条件概率，表示为

式中：(α)为路径时间预算.

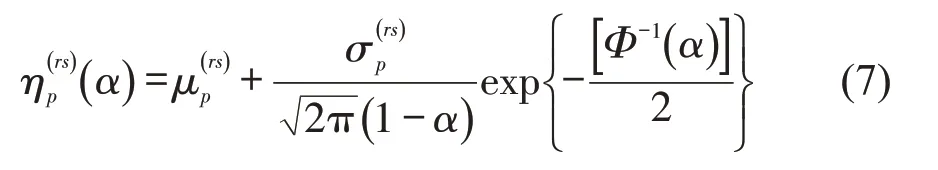
对于确定的置信度α，路径时间的不确定越大(即越大)，TTB 越大，METT 也越大.TTB 强调了能到达终点的路径时间，而METT 更强调TTB 时间内到达不了会产生什么结果，更好地描述了不确定性条件下的出行风险，为风险厌恶型的出行决策提供参考依据.

1.3 出行票价

根据民航局发布的《民航国内航空运输价格改革方案》《进一步完善民航国内航空运输价格政策有关问题的通知》，从2018年1月开始，只要有5家航空公司参与运营的国内航线，都将实施市场调节价，可以上调不超过10%的票价.由于航空属于稀缺资源，航班的价格对供需关系比较敏感.从各航空公司历史票价可以看出，同一条航线，旺季比淡季票价高.

因此，本文假设旅客出行需求量增加会促使航空公司提升机票价格，且价格与旅客人数呈线性关系.对每个旅客，出行票价为H为

式中：fa为路段a流量；kh、bh为费用的系数.对地面交通来说，出行费用不随旅客人数的变化而改变，即kh=0.

1.4 机场服务水平

机场群系统中，旅客出行必然会经过机场.而机场服务水平直接影响出行成本.旅客在机场出发时，需要办理登机手续、行李托运、安检、护照检查、登机；从机场到达时，涉及提取拖运行李、护照检查等.根据IATA 对机场服务水平的评价体系，上述各环节耗时越短，旅客对服务满意度就越高.然而，每个环节的耗时都会随着机场人数的增加而增加.此外，大机场航线网络更通达，航班频次更密集，固定等待的时间短；小机场航班频次低，固定等待的时间长.

因此，本文假设在机场容量范围内，旅客在机场停留时间与机场服务总人数承线性关系，超出机场容量时，旅客在机场停留时间为一固定且较大的数值，即

式中：Q为机场容量；kd，bd为机场服务水平的系数，大机场的bd小于小机场的bd；Ω为固定且较大的数.

2 配流模型求解

机场群系统中旅客出行选择可表示为一条由不同路段组成的路径.每条路径的起讫点为出发到达城市对.机场群系统均衡配流问题为固定需求下，出行时间与费用不确定的用户均衡问题.本文出行路径选择采用Logit 模型，且假设感知偏差服从Gumbel分布，某条路径被选择的概率为

式中：θ与感知偏差大小成反比，反映人们对网络阻抗的认知程度；l为路径的序号变量；、分别为起点r与终点s间路径p、l上的出行成本.

起点r与终点s之间的出行需求为q(rs)时，用户均衡模型等价的凸规划为

式中：为起点r与终点s之间路径p的流量；为所有路径流量组成的向量；ta(x)为路段a在流量为x时的行程时间.

定理1式(11)与式(10)等价.

证明 式(11)的拉格朗日函数为

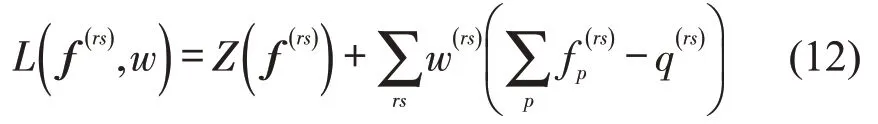
式中：Z(f(rs))为用户均衡模型需要优化的目标函数；w(rs)为拉格朗日乘子.

Z(f(rs))最小时有

式中：1 表示OD 对上的第p条路径经过路段a，0 表示p不经过a，因此有

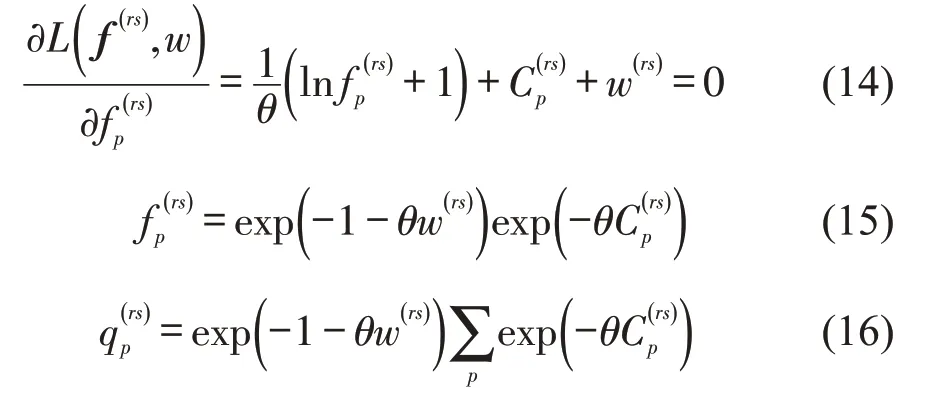
证毕.

上述均衡条件可表达为变分不等式，即寻找向量u*，使得

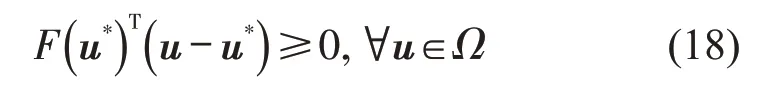
式中：y为构造变分不等式的中间变量；u=；

变分不等式已有多种求解方法，而投影收缩算法收敛速度较快，故采用该算法求解，如图1所示.

图1 变分不等式求解流程图Fig.1 Solution flow of variational inequality

图1中，PΩ为投影，PΩ(v)=Argmin{||u-v|||u∈Ω}，:=为赋值操作，所有变量的下标k为第k次迭代，β为对F(u) 线性变换的系数，r为对β调整的系数，μ为对β调整的边界值，为投影结果，d(·) 为步长，φ为步长的系数，Niter为算法最大迭代次数.基于上述算法可求解各路径的流量f(rs).

3 算 例

算例交通网络如图2所示.旅客从R点出发至S点，M1～M4为机场，L1～L3为高铁站，M与L之间为地面交通，L之间为轨道交通，M之间为空中航线.

实验中，设定一个评价指标，即机场饱和度ψ，定义为机场旅客流量f与旅客容量Q之比，即

假设有1 000 单位RS 间的出行需求，机场M1为大机场，往M4方向的容量为600，机场M2、M3为小型机场，容量为400.β=0.15，n=2，休闲型旅客ω=21.2(元/h)，ω的取值依据为2019年城镇居民人均可支配收入42 359元，每年工作250 d，每天工作8 h.其他参数如表1所示，路径时间与机场服务水平的单位为h，小型机场的服务水平相同，大型机场由于航线更多，kd和bd值更小.kh、bh、kd、bd等参数取值是为了使算例接近真实情况，例如，当机场M1客流量为500 时，票价为1 634 元，在机场停留时间为1.9 h.M2、M3由于航空公司运营等因素的差异，票价可能存在不同.

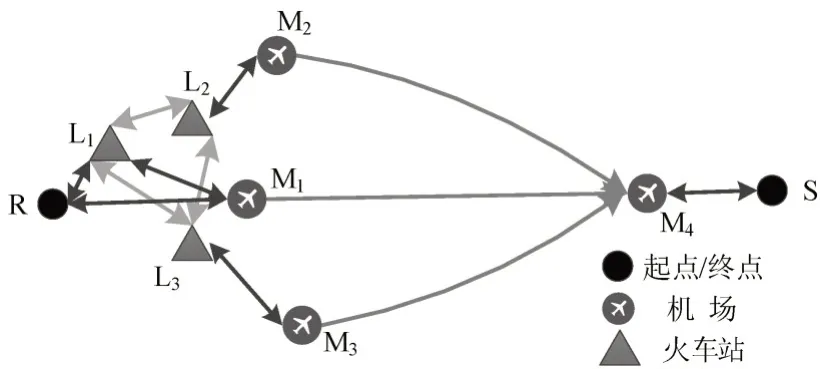
图2 机场群系统交通网络图Fig.2 Transportation network in a airport group

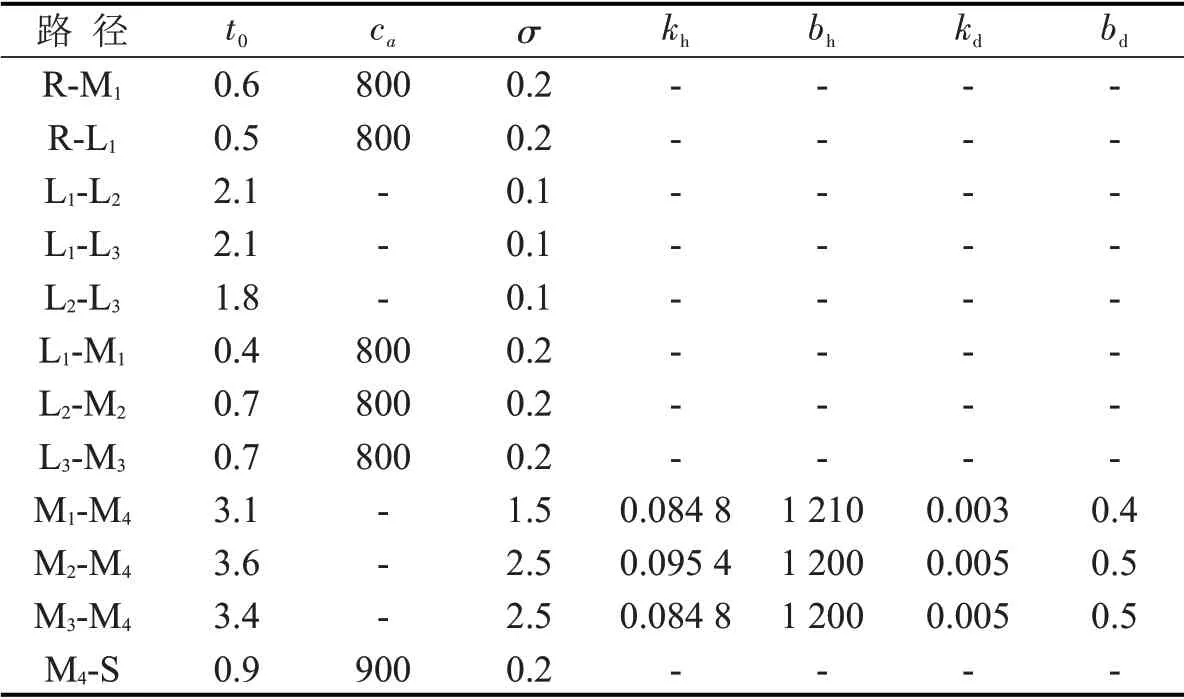
表1 路段参数Table 1 Properties of routes

情形13 个机场的流量分别为565、210 和225，出行成本都为76.4.结果表明，本文提出的配流模型可有效求解均衡状态，且最终成本同时到达最小.由均衡状态结果可知，3 个机场的流量差距较大，这是因为从M1机场出发的航线路段时间少，延误风险小，而M2和M3机场出发的航线路段时间长，延误风险高，故旅客更多地选择从M1机场出发.

情形2基于上述相同的参数，各个机场的饱和度为94.17%、52.51%、56.24%.此时，机场M1过于繁忙，机场M2和M3利用率不足.由于小型机场航班数量较少，利用合理的管理与技术手段对其进行编排容易减少延误风险.在本情形中，同时减小M2-M4与M3-M4间的σ至0.3，即减少小型机场的延误风险，各机场的饱和度及旅行出行成本如图3所示.由图3(a)可知，随小型机场延误风险降低，大型机场拥堵缓解，小型机场资源利用率提高.同时，旅客的出行成本也随之降低，如图3(b)所示.

情形3情形1中从各机场出发的票价差别较小，对客流分布的影响有限.将表1中M3-M4的kh逐渐降低以模拟机票价格下降.由图4可知，降低小型机场出发票价可提升该机场的资源利用率，同时减轻其他机场负荷.该结果表明，对于航空公司而言，降低从小型机场出发航班的票价，有效吸引更多旅客从小型机场出发，不仅可以提升小型机场的盈利能力，还可降低大型机场因延误造成的损失.

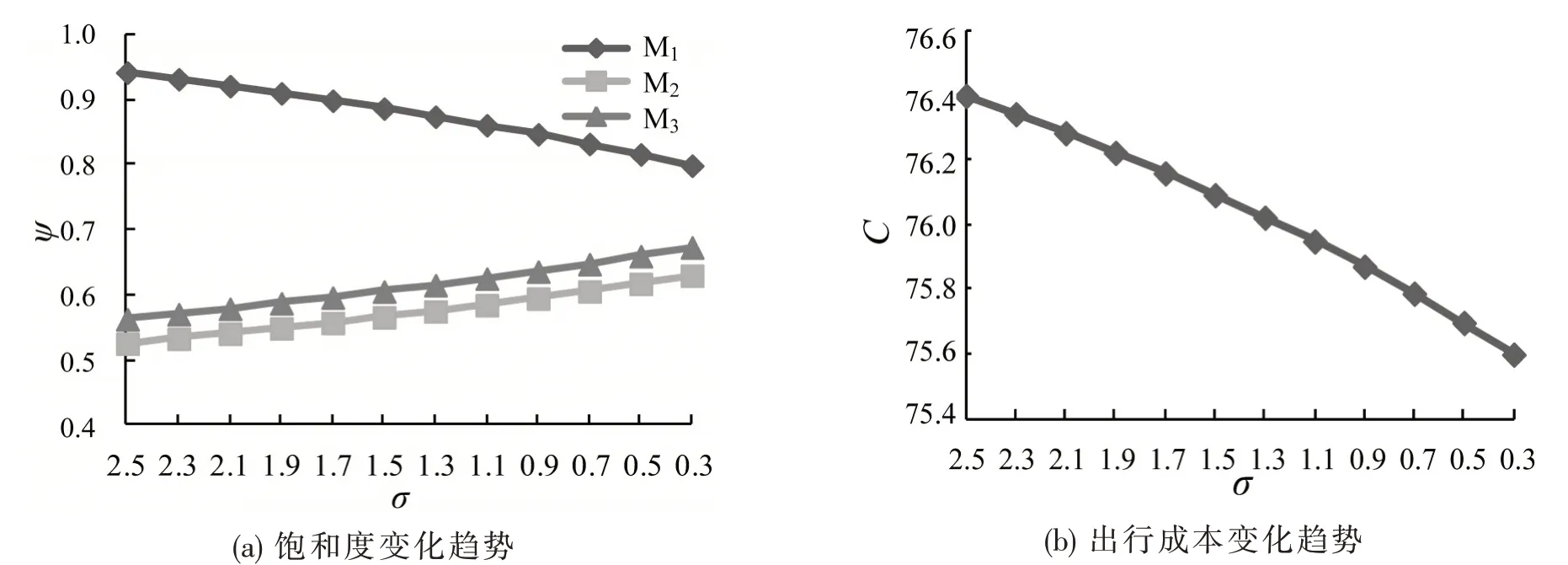
图3 各机场的饱和度、旅客出行成本与小型机场延误风险的关系Fig.3 Saturations of airports and travel costs of different delay risk of small airports

图4 各机场的饱和度、旅客出行成本与小型机场出发票价的关系Fig.4 Saturations of airports and travel costs of different travel costs of small airports

情形4情形1 中各机场服务水平差别不显著.将表1中M3-M4的kd逐渐降低以模拟机场服务水平提升.由图5可知，提升小型机场服务水平与降低小型机场出发票价效果类似.现实中，大型机场值机、安检等流程耗费时间越来越长.情形4 结果表明，优化小型机场各类流程，减少旅客花费时间，可促进客流在机场间更合理地分布，综合提升旅客在各类机场出行的体验.

情形5对于商务型旅客，设ω=26，其他条件与情形1 相同.3 个机场的流量分别为587、200和213，饱合度分别为97.87%、49.89%和53.31%.可见，时间价值较高的商务型旅客倾向于选择航线网络更为通达的大型机场.

情形6与传统用户均衡(User Equilibrium,UE)模型对比.UE 模型未考虑出行路径的不确定性，即情形1 中所有σ=0.基于UE 模型，各机场的均衡状态流量为739、111 和150，饱和度分别为115.00%、37.36%、40.20%.现实中，人们决策会考虑机场过分拥堵造成的出行成本上升，而UE模型未能很好地体现这一特点.因此，本文提出的模型能更好地描述客流分布规律.

图5 各机场的饱和度、旅客出行成本与小型机场服务水平的关系Fig.5 Saturations of airports and travel costs of different service standards of small airports

4 结 论

在空中与地面交通路径时间不确定环境下，本文全面考虑机场群系统中影响旅客路径选择的4个重要指标，即路径时间、机场停留时间、出行票价和旅客类型.基于上述指标构建均衡配流模型，并对其求解从旅客个体路径选择偏好构建机场群系统全局的客流分布状态.由算例结果可知，不同指标条件下，客流分布状态均会改变，且与经验或事实相符，证明了均衡配流模型刻画机场群系统客流分布规律的有效性及正确性.本文模型可进一步结合累积前景理论，从行为决策的角度探索机场群旅客出行的路径认知规则.