基于多车协作优化的冲突消解模型
成 英,赵建有,汪 磊
(1.天津职业技术师范大学汽车与交通学院,天津300222;2.长安大学汽车学院,西安710064;3.天津中德应用技术大学汽车与轨道交通学院,天津300350)
0 引 言
近年来,为提高交叉口行驶安全性,国内外学者提出基于间隙接受模型,基于运动学的矢量图法,基于资源锁的冲突表算法,先到先服务(FCFS)模型等冲突消解算法[1-3],基本思想是以假设路口优先级为前提,主要采用减速或等待的保守驾驶策略规避冲突,没有考虑车辆间相互协作功能,限制了自动驾驶车辆的路口通行潜能.
目前,智能车辆与智能交通设施可以实现车与车、车与交通设施之间的数据交互,面向自动驾驶环境的多车协同控制成为研究热点.王庞伟等[4]在车—车通讯条件下,基于滑模控制设计多车协同响应的避撞方法,通过分配前、后车辆的加速度,实现协同避撞的目的.L.EVIN[5]使用混合整数线性规划模型协调自动驾驶车辆在冲突点的通过时间,并借助滚动时间窗的方式优化最优解.F.AYAZI[6]建立基于混合整数线性规划的自动驾驶交叉口控制模型,优化自动驾驶环境下交叉口的车辆到达时间和行驶车速.然而,当多辆车从不同方向接近同一路口时,缺乏对某种危险驾驶行为协同响应的研究.本文提出基于多车协作优化的冲突消解模型,通过无线通信技术实现两车的状态信息共享,将多车看成一个整体,利用控制理论等方法计算分配给相互冲突车辆的期望速度规划,达到协作行驶的目的.同时,在多车协作行驶未能规划出联合行动或者协作响应超时,系统将以非协作行驶作为输出,保证自动驾驶车辆冲突消解的稳定性和鲁棒性.
1 冲突分析与判定
多个车辆即将进入交叉口冲突区域时,系统首先使用通行侵入区域时间差PET(Post Encroachment Time)参数对交叉口潜在冲突进行评估,作为描述车辆之间任意角度碰撞的重要指标[7-8].
Tpet参数定义为前车离开交叉口区域与后车进入交叉口区域的时间差.

式中:TV11为前车V1 进入侵入区域的时间;TV12为前车V1 驶离侵入区域的时间;TV21为后车V2 进入侵入区域的时间;TV22为后车V2 驶离侵入区域的时间.
参考文献[8]确定的交叉口冲突阈值,Tth取值3 s,将实时计算的Tpet与冲突阈值Tth比较,进行交叉口交通冲突识别.当Tpet>Tth时,表示不存在潜在冲突,车辆保持原有速度通过交叉口;当Tpet≤Tth时,表示存在潜在冲突,车辆需要采取冲突消解策略避免碰撞危险.
2 系统框架
假设无信号路口所有车辆均配备V2X(Vehicle to X)通信系统,且通信效果良好,每个车辆能够实现车—车通信,实时、准确地获取通信范围内周围车辆的运动状态信息,车辆通行过程中无行人和非机动车干扰.
本文提出基于多车协作优化的冲突消解方法,如图1所示.通过车—车通信将行驶在道路上的车辆协同行驶,使之成为一个系统整体运行;若多车协作未能规划出联合行动或者协作响应超时,系统将以非协作行驶作为输出,保证自动驾驶车辆冲突消解的稳定性和鲁棒性.
系统通过车—车通信(Vehicle-to-Vehicle Communication,V2V)获得周围车辆的实时驾驶状态信息,车载传感器实时监测目标车辆驾驶状态信息.当判断无信号路口存在潜在冲突时,给冲突车辆发送协同请求,当车载冲突消解单元协同行驶时,以优化通信范围内车辆联合收益为目标,实现群集中车辆间的自主协同行驶;当冲突车辆无法协同时,仅考虑目标车辆个体收益,采取减速避让的保守策略避免冲突.底层控制单元执行系统发出的车辆操控指令,更新通信范围内的所有车辆状态信息,使不同行驶方向的车辆可以同时相互穿插地通过交叉口,提高道路通行能力.

图1 无信号交叉口自动驾驶车辆冲突消解方法Fig.1 Conflict resolution method for autonomous vehicles at non-signalized intersections
3 模型构建
3.1 模型目标函数
当交叉口车辆进入冲突区域时可能发生碰撞危险,一般通过加速、匀速、减速3种行驶策略避免危险,相互冲突车辆的每一组不同加速度组合都是冲突消解中的策略之一.冲突消解问题用3组元素描述,参与者表示为第i辆目标车辆Vi、第j辆冲突车辆Vj,即S={Vi,Vj},i∈N,j∈M,其中,N为目标车辆总数,M为冲突车辆总数.将目标车辆Vi的动作空间定义为AVi={aAcc,aCon,aDec},其中,aAcc为加速,aCon为匀速,aDec为减速,冲突车辆Vj的动作空间定义为Avj={aAcc,aCon,aDec},用笛卡尔积A=AVi×AVj表示联合行动空间.多车协作目标是为系统选择一个联合行动,使得整体驾驶收益最大,其中,联合行动收益由目标车辆收益和对冲突车辆影响两部分构成.将冲突消解问题构建为带约束的非线性优化模型,则交叉口冲突消解的总收益为

式中:(ai,aj)为第i目标车辆与第j冲突车辆的联合行动空间;vi(t)、vj(t)、ai(t)、aj(t)分别为t时刻第i目标车辆与第j冲突车辆的速度、加速度;Li(t)、Lj(t)为t时刻车辆i、车辆j到冲突点的距离;fVi(ai,aj)、fVj(ai,aj)为车辆联合动作时第i目标车辆与第j冲突车辆能够获得的驾驶效益;p为车辆间合作系数,取值[0,1],p=0 表示车辆间为非合作关系,p=1 表示车辆间为完全合作关系;t0、td为车辆进入和离开冲突区域范围的时间,即加速度规划起止时间;αmin、αmax为车辆控制所允许的加速度限值;vmin、vmax为交叉口所允许的车辆行驶速度限值.
3.2 驾驶收益计算
驾驶收益不仅与车辆所处状态有关,还与车辆间冲突程度有关,故使用安全性、快速性和舒适性指标来体现决策主体的驾驶收益函数[8].
(1)安全性.
安全是交叉口通行过程避免碰撞的首要指标.假设ΔT表示车辆到达冲突点的时间差,ΔT越小,表示车辆冲突激烈程度越大,驾驶收益越小.安全性收益计算为
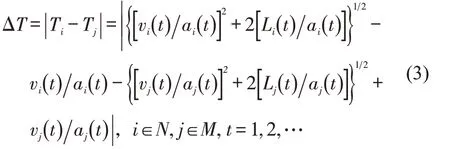
式中:Ti、Tj分别为t时刻第i目标车辆与第j冲突车辆到达冲突点的时间.
(2)快速性.
快速性收益指车辆期望以较快的时间通过交叉口,通过速度变化体现快速性收益,即

式中:Δvi、Δvj为车辆i、车辆j在Δt时间内的速度变化.
(3)舒适性.
舒适性收益主要考虑车辆纵向加速度变化,加速度变化过大会导致舒适性下降,故选择加速度变化量反应.舒适性收益为
式中:Δai、Δaj为车辆i、车辆j从第t-1 时刻到第t时刻的加速度变化,包含冲突消解策略集中的所有动作行为.
综上,每个车辆驾驶收益函数表示为
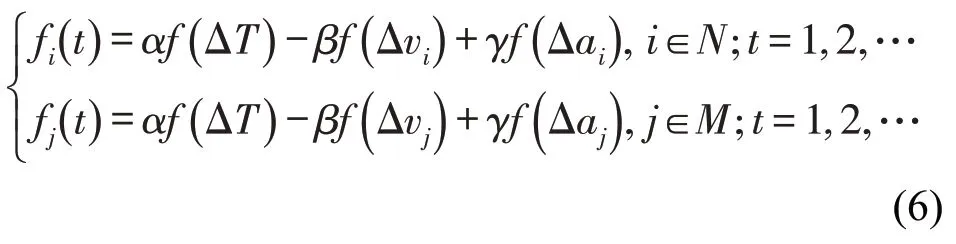
式中:f(⋅)为归一化计算;α、β、γ分别为安全性、快速性、舒适性指标权重,满足α+β+γ=1.
3.3 模型求解
针对带约束的非线性优化问题,采用遗传算法(Genetic Algorithm,GA)进行求解,算法中每代最优解由适应度函数保存,经过几次迭代,能够得到“全局”最优解,遗传算法的适应度函数[7]表示为

求解流程如下所示:
Step 1 预设遗传迭代总次数Γ,种群规模B,优化模型约束满足式(2).
Step 2 根据约束条件随机产生B组遗传个体,组成初始种群.
Step 3 根据车辆运动模型式(8)更新车辆位置、速度等,分别得到各遗传个体(加速度组合)下冲突区域车辆的行驶轨迹.
Step 4 利用GA算法分别求解各遗传个体下的加速度优化解,得到冲突区域车辆最优参考行驶轨迹,并根据式(6)得到交叉口整体驾驶收益.
Step 5 根据式(7),分别评价并标记各遗传个体.
Step 6 评判所有遗传个体,如果到达迭代总次数Γ,则输出最优个体及其最优解,并停止计算;否则,进入Step 7.
Step 7 以适应度函数值为依据选择再生个体,并对其进行交叉变异生成下一代新个体,汇总得到新一代种群,进入下一次迭代,每一代迭代计算均需要满足约束条件,并返回Step 3.
求解过程中,将车辆轨迹估算与启发式优化算法相互嵌套,即通过得到新遗传个体,根据车辆运动模型式(8)更新车辆轨迹估计.Li(t)、vi(t)及ai(t)为车辆i在时刻t的位置、速度与加速度,满足

式中:Li(t+1)、Lj(t+1)、vi(t+1)、vj(t+1)分别为车辆i、车辆j在下一时刻的位置、速度;φi、φj分别为车辆i、车辆j的航向角度.
4 实验验证
4.1 仿真场景
假设无信号交叉口车辆V1由南向北直行行驶,车辆V2由东向西直行行驶,车辆V3由北向东左转行驶,可能形成冲突点1、冲突点2、冲突点3,如图2所示.运用matlab 进行数值模拟仿真实验,为尽可能得到全局范围内的最优集,在遗传算法的种群初始化、选择、交叉和变异中保证最优集的有效性,取种群为50个个体,交叉概率为0.8,变异概率为0.05,运算最大代数为200 代,步长为0.5 s.仿真实验参数设置如表1所示.
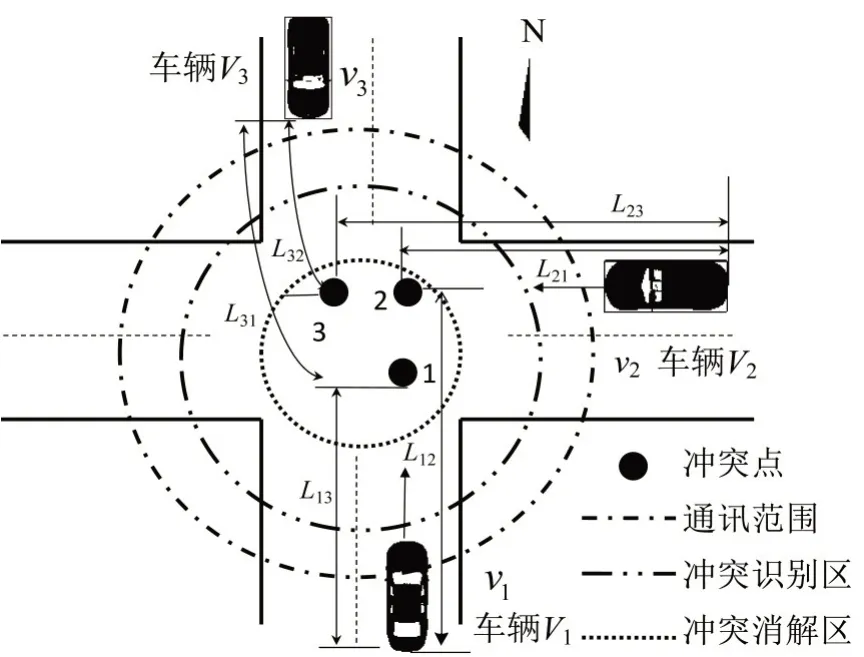
图2 无信号交叉口自动驾驶车辆冲突消解仿真场景Fig.2 Experiment of collision resolution of vehicles at intersections
4.2 实验结果
以目标车辆V1与冲突车辆V2形成的冲突点2为例进行结果分析,当系统判断存在潜在冲突(TPET≤Tth)时,车载冲突消解单元选择协作行驶,开始执行冲突消解优化算法,如图3所示.

表1 仿真实验参数设置Table 1 Parameter setting of simulation experiment
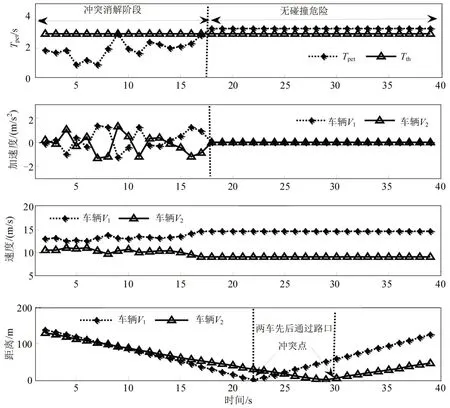
图3 车辆V1 与V2 协作行驶时冲突消解仿真结果Fig.3 Conflict resolution result of vehicle V1 and V2 by cooperative driving strategy
由图3可知,冲突消解时长为18步长,目标车辆V1提高车速,在T=11 s 时率先通过冲突点;冲突车辆V2降低车速,在T=15 s 时滞后通过冲突点.使得不同行驶方向的车辆可以同时相互穿插通过交叉口,有效解决路口冲突时通行权分配问题,避免碰撞危险.
为进一步验证模型的鲁棒性,选择传统非协作冲突消解算法[3-4]与模型对比.非协作行驶时,假设冲突车辆V2具备优先通行权,目标车辆V1以个体收益为目标执行冲突消解算法.如图4所示.

图4 车辆V1 与V2 非协作行驶时冲突消解仿真结果Fig.4 Conflict resolution result of vehicle V1 and V2 by non-cooperative driving strategy
由图4可知,冲突消解时长为22步长,冲突车辆V2保持原有速度,在T=13 s 时优先通过交叉口,目标车辆V1采取减速避让策略,在T=16 s 时滞后通过冲突点.
对协作式与非协作式冲突消解模型进行多次实验,对改善路口冲突消解时间、整体收益、平均速度、平均收益及不良加速度方面的性能进行对比分析,结果如表2所示.

表2 协作式与非协作式冲突消解模型的对比分析Table 2 Analysis of cooperative and non-cooperative conflict resolution models
由表2可知:两车冲突消解过程中车辆V1平均收益为0.061 9,车辆V2平均收益为0.089 0,整体驾驶收益有所提高,各利益体间的收益更加均衡;与非协作式冲突消解相比,冲突消解时间缩短4个步长,交叉口平均单车延误减少约1 s,平均减少量约为5%;多车冲突消解过程中各车辆间的平均收益更为均衡,冲突消解时间缩短8 个步长,交叉口单车平均延误减少约1.5 s,平均减少量约为5%.因此,基于多车协作优化的冲突消解方法,对于提高道路通行能力具有一定意义.
5 结 论
考虑无信号交叉口多个自动驾驶车辆共享路权的局面,本文提出一种基于多车协作优化的冲突消解方法,优化了自动驾驶车辆冲突时的速度规划,实现群集车辆间的自主协同行驶.本文的主要贡献在于:
(1)冲突消解主要遵循无碰撞要求,通过最大化联合行动的驾驶整体收益进行速度规划,使得不同行驶方向的车辆可以同时相互穿插地通过交叉口,有效解决了交叉口道路通行权不清楚时的冲突消解问题.
(2)车载冲突消解单元集成了协作与非协作规划的两种行驶模式,在前者未能规划出联合行动或者协作响应超时,系统将以非协作行驶决策作为输出,保证自动驾驶车辆冲突消解的稳定性和鲁棒性.
(3)通过设置协作与非协作式冲突消解仿真实验,基于多车协作优化的冲突消解模型实现整体收益最大化,且各利益体间的收益更为均衡,与传统非协作冲突消解相比冲突消解时间减少,交叉口单车平均延误减少约1~2 s,平均减少量为5%左右,提高了道路通行能力,验证了本文模型的有效性与鲁棒性.需要指出的是本模型仅针对交叉口多车协同时进行速度优化,并未对车辆行驶路径规划作深入研究,该问题可作为未来研究的重点,对于提高自动驾驶车辆交叉口通行能力具有重要意义.

