指引路径规划模型的建模与仿真验证

赵 琦，曾 烨，张立立，王 力

(1.北方工业大学城市交通智能控制技术北京市重点实验室，北京100144；2.北京石油化工学院信息工程学院，北京102617)

0 引 言

在城市道路交通系统中，指路标志是道路信息的重要载体，帮助机动车驾驶员方便快捷地抵达目的地[1].合理地规划指路标志的布设位置不仅能正确引导驾驶员驾驶车辆，同时也是提升城市交通系统运行效率，改善路网交通流状态的必要手段.

学者就指路标志的布设方法进行了很多研究.肖国荣[2]基于各个OD(Origin-destination，交通出行的发生点和吸引点)对间出行者偏离最优路径的概率，提出一种定量评价指路标志规划方案合理性的方法，得到出行者偏离最优路径概率最小的指路标志布设方案.郭敏[3]基于树状图模型，建立了一种宏观的路网指路信息分配模型，指导城市复杂路网指路标志系统的整体规划，但未涉及具体路径指路标志的布设研究.黄敏[4]运用双圈覆盖法定义路网中的两种等级区域，基于Dijkstra算法对路网中的重要兴趣点(Point of Interest,POI)进行指引路径规划，保证指路信息的连续性，但不能避免指引路径中特定节点出现指路信息过载问题.有学者为提高指引路径规划模型的运行效率，采取启发式算法对现有规划模型进行改进.Zheng Jian[5]通过对比遗传算法和人工蜂群算法在指引路径规划中的应用，验证了人工蜂群算法在优化过程中具有更高的收敛速度.张腾[6]改进了人工蜂群算法的搜索策略，建立指引路径优化模型，优化同一路网中的多条指引路径，但同样未对指路信息过载问题进行研究.

现有研究大都忽略了路网特定节点发生指路信息过载问题，而该问题使驾驶员无法及时、有效地获取道路信息，带来不必要的安全隐患及寻路成本.因此，为有效避免指引路径中特定节点产生信息过载问题，优化指引路径的规划方案，本文将信息过载问题视为指引路径规划的重要影响因素，基于A*算法提出一种含有惩罚系数的指引路径规划模型.

1 问题描述

兴趣点是路网中重要的地理位置信息，包括人们出行密切相关的地理实体，例如学校、商场等.2015年批准实施的中国《城市道路交通标志和标线设置规范》规定：根据指引地点的交通重要程度，宜在指引地点周边的1～3个交叉口处增设地点信息.然而，一旦某区域重要兴趣点比较集中，指路标志又没有得到正确设置，容易引发该区域内特定节点(受附近重要兴趣点影响，需要增设过多指路信息的交叉口指路标志的设置位置)指路信息过载问题.

通过对指引路径规划方法进行研究，能够有效解决上述问题.指引路径是由路网道路及指路信息构成的路径，其中，指路信息是指路标志承载的特定信息，一般为区域内主要OD 对服务，可以向位于起点的驾驶员传递其所需的、与终点相关的地点信息，协助驾驶员对行驶路线进行规划.指引路径规划可视为基于路网拓扑结构，从指定起点出发，综合考虑指路标志布设成本，驾驶员寻路成本等重要因素，求解路网中实际成本最低，对指定终点可达性强的有向路段的集合.因此，路网拓扑结构、指路标志、兴趣点三者之间相互影响.

1.1 路网表示

为直观展示路网拓扑结构，本文基于图论，用节点—弧段表示路网结构[7].G表示区域路网，G={N,A}；N为路网G的节点集合，N={ni}，ni为节点；A为路网G的路段集合，A={aij=(ni,nj)}，aij表示起点为ni，终点为nj的路段；P表示路网中重要兴趣点集合，P={pi}；R(ni,pi)表示从节点ni至兴趣点pi的指引路径，R(ni,pi)={aij,ajk,…,aopi} 表示指引路径的路段集合，i、j、k、o分别为节点ni、nj、nk、no，pi为兴趣点.

为利用路网拓扑结构进行指引路径规划，对真实路网进行栅格化处理，如图1所示.图1(a)表示一个G0={N0,A0} 的简单路网环境，N0为节点集合，N0={n1,n2,n3,n4,n5}，A0为弧段集合，A0={a12,a23,a24,a25}，在节点n2处需设置指路标志.图1(b)是经过处理的简单路网示意图，节点N0的坐标值由节点所在栅格坐标决定，弧段A0的长度由对应节点间的距离决定.

1.2 目标函数

影响指引路径成本W的关键因素包括指引路径长度和指路标志数量[7]，故综合考虑这两种成本，即W(L)和W(S)，求解最小成本的指引路径.由于路径长度L和指路标志数量S的量纲不一致，采用min-max标准化对两种成本进行归一化处理[4].

式中：W(L)为指引路径R(O,D)的路径长度成本函数；O为路径起点；D为路径终点；L[R(O,D)]为指引路径R(O,D)的路段总长度；W(S)为指引路径R(O,D)上指路标志数量成本函数；S[R(O,D)]为指引路径R(O,D)中指路标志总数量.

图1 路网栅格化处理示例Fig.1 Example of rasterized network

参考文献[8]，假设起点O至终点D的直线距离为V，则max(L) 的值为2V；假设路网中路段平均长度为l，则max(S) 的值为2V/l.指引路径总成本W表示为

式中：α，β分别为W(L)、W(S)在W中所占权重.参考文献[8]，将α、β分别取0.5，即认为指路标志数量和指引路径长度对目标成本函数的影响相同.

2 模型构建

2.1 A＊算法

A*算法是由Hart[9]提出的一种启发式搜索算法.该算法在Dijkstra 算法的基础上，加入计算从当前节点到终点成本估计值的启发函数h(i)，具备更高的搜索效率和灵活性[10].A*算法的主函数——估价函数f(i)为

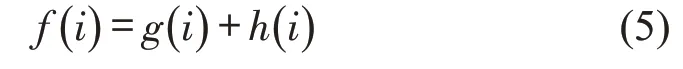
式中：g(i)为指引路径起点O至节点ni所花费的成本，为当前成本；启发函数h(i)为节点ni到终点D的指引路径估算成本.当h(i)值不大于节点ni到终点D的实际成本值时，算法不会遗漏最优指引路径的解.

参照式(3)，建立指引路径规划模型的估价函数f(i) 为

根据研究问题的不同，A*算法一般使用曼哈顿距离、欧几里得距离或切比雪夫距离建立启发函数h(i)[11].为确保h(i)小于节点ni至终点D的实际成本，且车辆在城市道路中一般朝4个方向移动，本文选取曼哈顿距离构建启发函数h(i)[12]为

式中：Dx，Dy分别为终点D的横、纵坐标；ix，iy分别为当前节点ni的横、纵坐标.

2.2 惩罚系数

从f(i) 的组成来看，指引路径长度越短，路径上指路标志越少时，路径成本W越低.现有研究表明，指路标志版面承载的指路信息超过5 条时，会给驾驶员带来过高的信息负荷，使其不能及时地处理指路信息，错失寻路时机[13].因此，对指引路径进行规划时，应当避开可能产生指引信息过载的特定节点，优化指引路径方案.故迫使算法改变当前搜索方向，放弃访问指路信息过载的节点，在原算法中增加对寻路成本f(i)的惩罚系数M，原寻路成本函数演变为

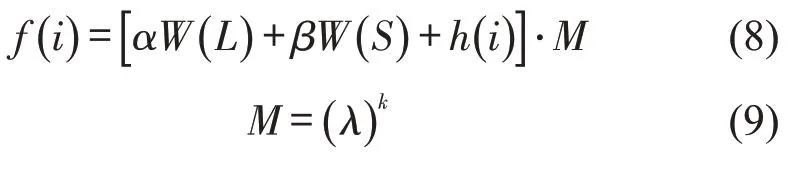
式中：k为节点指路信息过载的指示参数，当节点指路信息过载时，k值为1，否则为0；λ为惩罚参数，当λ取值足够大时，若节点ni存在指路信息过载问题，其寻路成本f(i) 的值会突增，算法随即放弃访问节点ni.为确保模型最终输出的指引路径中不存在指路信息过载的问题，将λ取值为10.

2.3 节点信息

为获取有向路段集合R(O,D)的寻路成本f(i)、当前成本g(i)和估算成本h(i)的值，模型需要遍历路网中各个节点，并读取节点存储的成本值.路段aij的当前成本g(aij)，估算成本h(aij)，估价函数f(aij)分别为

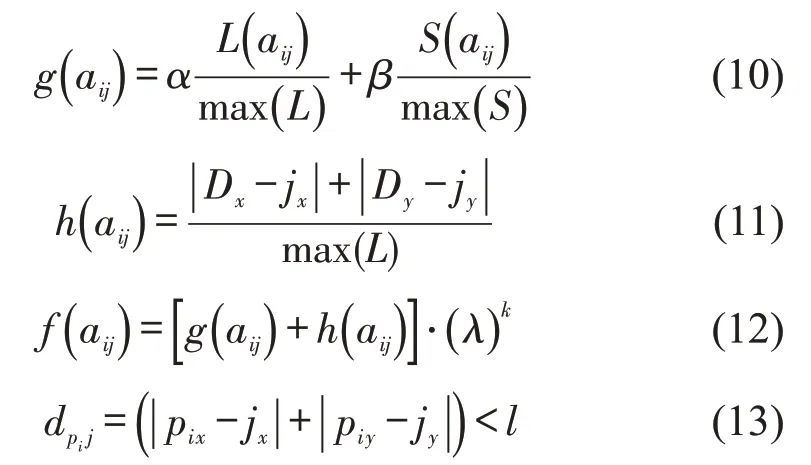
式中：L(aij)为路段aij的长度；S(aij)为路段aij交叉口处增设的指路标志数量，值为1；pix、piy分别为兴趣点pi的横纵坐标；jx、jy分别为节点nj的横纵坐标.根据《城市道路交通标志和标线设置规范》中关于地点识别标志的规定(需要在重要兴趣点周边1～3 个交叉口处设置指路信息)，假设兴趣点pi与交叉口节点nj的距离dpi j满足式(13)时，在节点nj处相应地增设一条地点指路信息.

交叉口指路标志一般包含3条道路信息，交叉口需要同时增设终点的地点信息，故某个交叉口节点ni增设了3条及以上指路信息时，该节点的k值为1，否则k值为0.

设定节点信息后，需要对路网进行栅格化处理.将有向路段aij分成m个栅格，每个栅格的单位长度保持一致，同时将路段aij的成本分配至各个栅格上，除交叉口节点ni外，交叉口节点nj成本为wj，其余栅格成本均为wij.

2.4 算法流程

指引路径规划算法基于VB6.0平台实现，算法搜索从起点O开始，根据f(i)值确定搜索方向，直至搜索到终点D.算法流程如图2所示.

3 仿真验证

(1)仿真分析.

本文利用VB6.0 对VISSIM 实验路网进行二次开发，以展示指引路径规划模型的应用过程，实验路网如图3所示.路径起点O为路网中高架路的出口匝道，路径终点D为某重要兴趣点的入口处.

通过COM 接口获取实验路网内路段及节点信息，得到起点O距终点D的直线距离V、路段平均长度l、节点ni数量、路段aij数量，如表1所示.

利用不含惩罚系数和本文提出的带惩罚系数的指引路径规划模型，对实验路网中指定的OD对求解最优指引路径，分别得到指引路径规划方案1、方案2，如图4所示.

分析两种指引路径方案及VISSIM仿真结果，得到两种模型输出路径规划方案的对比情况，如表2所示.其中，行程时间t为自由流情况下，车辆从起点O至终点D所耗费的时间，指引路径的目标成本W为

依据上述实验结果发现：在指引路径规划模型中引入惩罚系数M后，车辆行程时间t下降1.93%，指引路径长度L减少289 m，同时避免了节点发生指路信息过载问题；但方案2需布设的指路标志比方案1增加1块，指引路径的目标成本值W上升2.65%.

图2 指引路径规划算法流程图Fig.2 Flowchart of guiding path planning

图3 实验路网结构图Fig.3 Structure diagram of road network for experiment

表1 实验路网静态数据Table 1 Static data of experimental road network

图4 指引路径规划方案Fig.4 Guiding path planning scheme

表2 两种模型的运行结果对比Table 2 Comparison of results between two models

(2)统计对比分析.

为验证两种模型得到的指引路径规划方案是否具有显著性区别，调整VISSIM 仿真中5 项关键参数值，进行100 次对照实验，各参数属性如表3所示.

表3 VISSIM 参数调整说明Table 3 Instructions of VISSIM parameters adjustment

利用SPSS 软件，进行配对T 检验分析实验结果，得到两种方案的行程时间相关系数为0.962，sig 值为0.04，这说明两方案之间存在很高的相关性和显著性区别.

由此可以得出，基于A*算法提出的指引路径规划模型在引入惩罚系数后，能够获取最优指引路径规划方案.虽然该方案的指引路径成本值W略大，但能够有效解决特定节点指路信息过载问题.

4 结 论

本文在传统A*算法基础上，在估价函数中引入惩罚系数，构建一种新的指引路径规划模型.该模型考虑到指路信息过载问题对指引路径实际成本的影响，改善指引路径的规划方法.通过仿真验证结果可知，基于本文建立模型得到的指引路径规划方案的路径成本虽略高于最低成本，但是能够有效避免指引路径上特定节点出现指路信息过载问题.这将为解决目前指路标志布设规划中存在部分节点指路信息过载问题提供方法依据.

本文所建立的模型只考虑了单个OD 对之间的指引路径规划，而现实中面临的是多个OD对之间的指路标志指引路径的优化问题.后续将在本文提出模型的基础上，针对这一问题展开研究.此外，未来还将利用驾驶模拟器及真实驾驶场景实验来验证模型的有效性.