基于票务数据的团体旅客出行目的推断

钱剑培，邵春福*，李 军,2，蔡 楠，黄士琛

(1.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京100044；2.中国交通通信信息中心交通运输信息化标准研究所，北京100011；3.南通市规划设计院有限公司，江苏南通226004)

0 引 言

Gong[4]指出现有工作可分为基于规则的方法、概率方法和机器学习3 类，其中，机器学习日益成为主流.一般研究多从个体单次出行视角出发，基于单日数据挖掘个体人口统计[5]、出行时间[6]、目的地[7]等特征与出行目的潜在关系.Allahviranloo[8]从个体出行序列视角出发，考虑前后活动类型的次序信息.上述方法同属于有监督分类，参数标定需要辅以回访调查，以提供真实出行目的.为在标签缺失场景下实现出行目的推断，Han[9]考虑其在出行链中的转换模式，将隐含状态解释为出行目的，得到的结果与经验相符.Wang[10]引入隐含狄利克雷分配(Latent Dirichlet Allocation,LDA)，对起讫点周边兴趣点聚类，得到若干主题，并将主题隐含语义与出行目的建立联系.LDA 主题模型已在诸多交通问题中得到应用，作为无监督方法，可以充分发挥海量数据对复杂行为模式的发现作用，突破将出行活动人为预设为几种规律性较强目的之局限.

上述研究面向的是市内居民日常出行，对于复杂的城际旅客出行，由于获取的票务数据等只能追踪上下车站点，无法沿用目的地空间信息和活动持续时间等特征.Janzen[11]提取频率和工作日占比等历史经验特征识别出4类目的；基于城际出行常见的结伴现象，Lu[12]引入成员人数、儿童及成年人比例等团体特征；Lin[13]考虑到成员信息中隐含社会网络关系，提出“同行网络”的概念，并引入复杂网络指标区分商务及旅游团.

本文面向城际团体旅客，考虑历史经验和结伴现象等特征，基于LDA 框架推断出行目的.首先，在LDA中嵌入出发时间生成模块，为推断提供额外信息并间接验证模型有效性；其次，提出团体旅客重建和语义化特征设计方法，通过计算特征共现得到主题聚类；再次，结合主题特征分布和出发时间分布标注出行目的；最后，利用票务数据对不同区域道路客运团体旅客出行目的构成及出行量演化影响因素开展案例研究.

1 嵌入出发时间的出行目的推断主题模型

1.1 主题模型视角下的团体旅客出行决策过程

采用LDA框架推断出行目的关键在于将团体旅客出行决策过程与文本主题生成过程类比.LDA本质是包含文档—主题生成过程和主题—词生成过程的概率图模型.有别于监督学习或聚类模型根据词计算损失或距离函数，LDA 通过直接计算不同主题下词共现规律，即主题—词分布实现主题聚类，同时得到每个文档主题分布.

受“同行网络”[13]启发，由于出行目的影响出行决策，不同出行目的将导致同行网络中产生不同成员组合.基于该视角，将文档、主题和词延伸为团体旅客(简称：团体)，出行目的(标注前仍称主题)和个体特征(简称：特征).由于特征可直接观察，只要能够识别同属一个团体的成员，即可以通过特征共现规律反推出行决策中对成员的选择是基于何种出行目的.

1.2 嵌入出发时间的主题模型构建与参数估计

LDA 中主题标注依赖于主题—词分布.考虑到成员特征各异，团体具有统一出发时间，而两者均与出行目的相关，因此，在LDA框架内嵌入出发时间生成模块，将主题—词分布的外延扩展为主题—特征分布及主题—出发时间分布，共同为出行目的标注提供信息.使用“盘子表示法”描述主题、特征及出发时间生成过程，如图1所示.

图1 嵌入出发时间的主题模型生成过程Fig.1 Generation process of topic model with start time embedded

假设主题数为K，团体数为M，团体m中第n个特征为wm,n，共Nm个，出发时间为tm.图1中，两个观察变量wm,n和tm均由隐变量主题k决定.首先对主题采样，特征wm,n对应主题记作k=zm,n，出发时间tm对应主题，两者服从同一个多项式分布，记为Multi(θm)，假设分布参数θm服从先验参数为α的狄利克雷分布Diri(α).得到各自主题后对wm,n和tm采样，wm,n有V个取值，任意v服从Multi(φk)，假设分布参数φk服从先验参数为β的分布Diri(β)；tm有L个取值，任意l服从Multi(ψk)，假设分布参数ψk服从先验参数为γ的分布Diri(γ).将wm,n和tm对应的观察变量样本集合记为W和T，对应的隐变量样本集合记为Z和Z′.

但是，在教学过程中，学生对中药标本利用率不高，存在以下问题：（1）不能较好地保管中药实物，因为中药固有的自然属性，学生不知道怎么保存，常有学生课上用完、课后就扔；（2）有的学生虽然将实物保存起来，但因保存方法不对，很快就会变质，加之学生嫌脏怕麻烦，课余时间也很少拿出来用；（3）在课后复习时学生也常拿出实物使用，但由于缺乏好的学习方法，常常看过即忘，学习效果不佳。

鉴于存在隐变量，采用马尔可夫蒙特卡洛模拟中的吉布斯采样算法(Gibbs Sampling)进行参数估计.算法核心是根据观察变量和隐变量的联合分布构造完全条件概率，进行J轮随机采样，在满足马尔科夫链收敛定理的前提下模拟真实分布.根据贝叶斯定理，zm,n和的完全条件概率分别为

式中：下标i=(m,n)；¬i(或¬m)为当前采样维度i(或m)以外的维度，不同维度间采样过程相互独立；和为当前主题k中特征和出发时间的计数值；和为当前团体m中特征和出发时间对应主题k的计数值.

由于多项式分布Multi(θm)、Multi(φk)、Multi(ψk)均与其先验狄利克雷分布Diri(α)、Diri(β)、Diri(γ)构成共轭分布，因此，参数θm、φk和ψk对应的后验分布服从狄利克雷分布，其中，上标为k、v、l的参数采用极大似然法估计，即

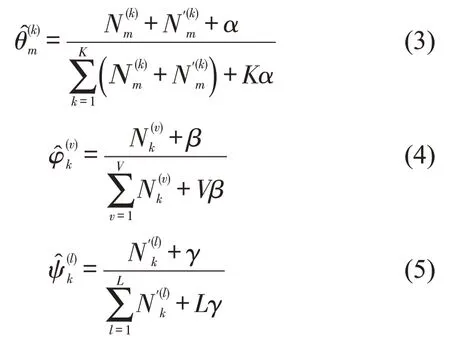
基于式(5)，给定新的团体，假设特征为，则出发时间的后验概率可以在主题分布预测结果基础上计算，即

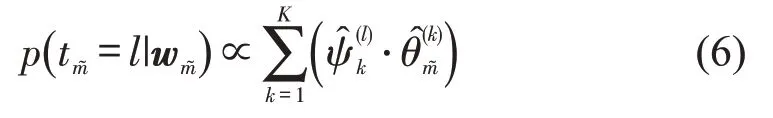
算法流程如图2所示.

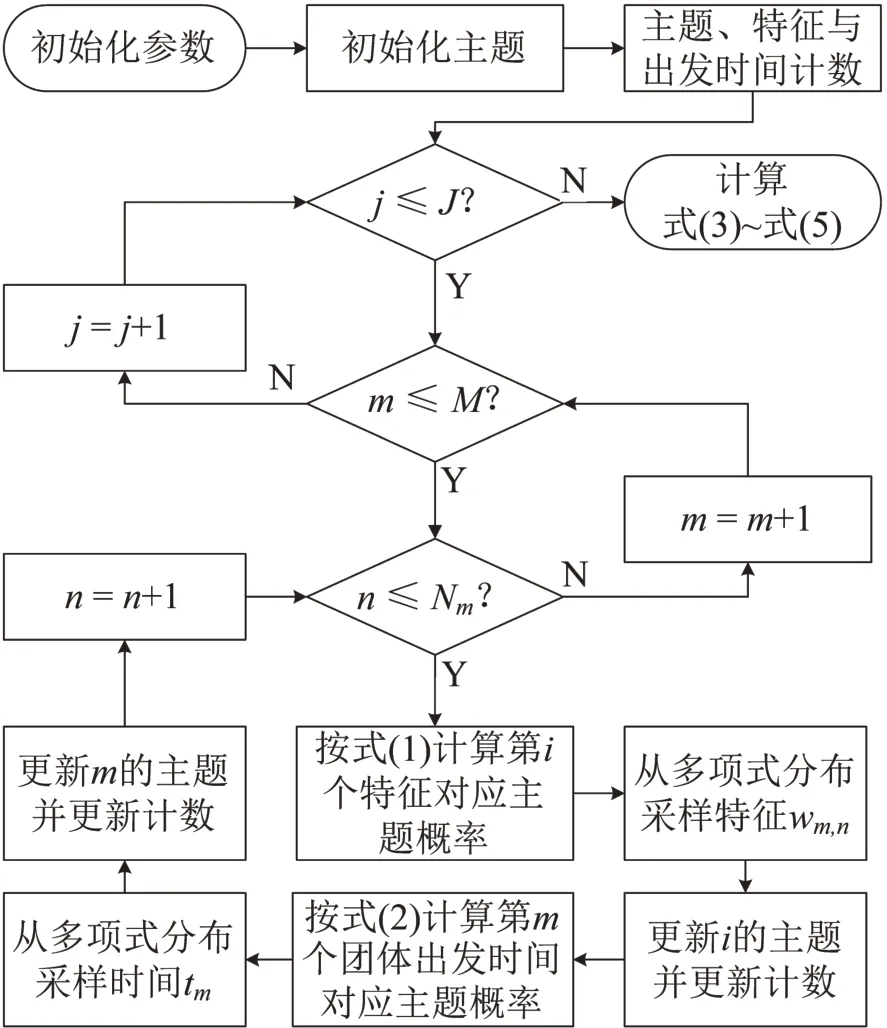
图2 Gibbs 采样算法流程Fig.2 Flowchart of parameter estimation by Gibbs sampling

2 面向主题建模的数据处理及性能验证

2.1 票务数据

采用经脱敏的北京市省际道路客运实名制联网售票数据(简称：票务数据)，包含2014—2018年3月出京购票记录.其中：实名制信息仅保留旅客辨识码、年龄和性别；其余所用字段包括检票日期、班次号、下单时间及目的地编号，旅客发送量年平均降低13.6%.选取目的地为山西省的样本进行案例研究，包含1 047 520 名旅客，共1 944 241条出行记录.

2.2 团体重建及特征设计

结伴出行通常由1人购买所有车票，故将具有一致毫秒级下单时间和班次号的2 名及以上旅客判定为团体旅客.利用上述算法共识别出320 474个团体，占所有记录的38.4%.主题模型采用词袋式特征，利用前述7 个字段提取3 类信息，计算成员特征后作离散化处理，使每个取值具有独立语义，结果如表1所示(删除少量相对特定出行目的倾向性不强的取值).其中，“年龄—性别二元组合”表示旅客社会关系，“上下文”衡量旅客关于某个目的地的历史经验，“潜在同伴数”借鉴复杂网络节点度的概念，表征同行网络规模.将出发时间分为6种：春运、节假日、周末、工作日、暑运周末及暑运工作日.

表1 特征设计及描述Table 1 Feature design and description

2.3 调查数据

为验证主题模型相较于既有方法在出行目的推断中的优势，于2020年1月依托某互联网平台实施面向道路客运团体旅客的出行调查.其中，出行目的划分为公务商务、放假返乡、旅游休闲及一般私务；其余问项参照票务数据所含信息进行设计.调查共获得540 份有效数据(简称：调查数据)，上述4 类出行目的分别占12.2%、34.4%、39.3%及14.1%.

2.4 基于调查数据的模型验证

按70%和30%将调查数据划分为训练集和测试集，选取神经网络(ANN)和梯度提升决策树(GBDT)作为基准模型.为反映样本分布不平衡条件下分类性能，采用受试者特征曲线下方面积(AUC)评价，如表2所示.

表2 基于AUC 值的模型对比Table 2 Model comparison using AUC values

ANN和GBDT等监督学习方法虽然能较好识别公务商务等目的，但对出行特征典型性较差的一般私务近似随机猜测(AUC为0.500)；相比而言，嵌入出发时间的主题模型分类效果更均衡，且除放假返乡外均优于基准模型.

3 道路客运团体旅客出行目的研究：以北京—山西为例

3.1 考虑出发时间预测的主题数选择

超参数K决定聚类精细程度.主题模型多以困惑度衡量最优K值：困惑度越小，对下一特征预测不确定程度越低，聚类效果越好.由于模型具备对出发时间预测能力，而这一能力强弱取决于聚类效果，故综合困惑度及预测精度确定K值，并间接验证聚类效果.由式(6)，以概率最高1 项和前2项出发时间作为输出，对应精度记为p1和p2.如图3所示.

当K=50 时，p1和p2同时取最大值，即0.638和0.909；困惑度随K增加而降低，在K＜35 时，下降较快，此后趋于平缓.为避免K过大时泛化能力不足，取K=50.

3.2 考虑特征分布与出发时间分布的出行目的推断

为缩短训练时间，取20%的票务数据训练模型.Gibbs 算法经历J轮采样完成老化过程后，按式(4)和式(5)计算，得到每个主题特征分布和出发时间分布，综合两者完成主题标注.过程及结果如图4所示.

图4中，左侧树状图将50 个主题分层聚类并标注为5种主要、9种次要类型出行目的，下方括号内数字为基于剩余80%数据得到的对应团体比例，任意团体m赋予唯一主题k=arg max；中间柱状图为每个主题特征分布；简化起见，右侧条形图仅列举主要类型中1 个典型主题的出发时间分布和最主要8项特征的取值概率.

图3 不同主题数取值情况下模型困惑度及出发时间预测精度Fig.3 Perplexity and precision of start time prediction in case of different values of K

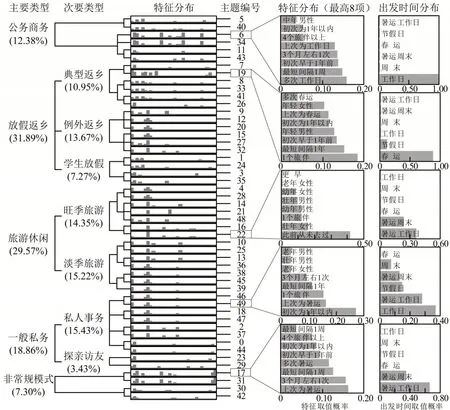
图4 出行目的推断结果Fig.4 Result of trip purpose inference

如图4所示，将青壮年为主且出行频率较高或出行间隔较短，出发时间多为工作日的主题标注为公务商务；具有初次出行时间较早、多次等特征，且以春运和节假日为主的出行标注为放假返乡；此前从未去过概率较高，且以节假日或暑运为主的出行标注为旺季旅游.不满足以上3类典型特征的出行标注为一般私务.有2 种例外情况，其一以老年夫妇结伴1年以上为特征，标注为探亲访友；其余被识别为非常规模式.主题17 和31 反映多人持续1年以上仅在暑运的频繁出行，主题30和42 反映最短间隔为1 个月且持续1年以上仅在节假日的频繁出行.因此，放假返乡和旅游休闲是北京—山西道路客运团体主要出行需求，占比大约为30%；一般私务和公务商务占比较低，非常规模式为7.3%.

计算詹森-香农散度(JS)比较训练集与测试集的主题分布得知，JS 为0.000 15，表明训练结果具有极强的可靠性.

3.3 不同区域出行目的构成及演化研究

2012年底，北京—太原高铁通车；2014年7月，太原—西安高铁通车.考虑高铁开通时序，将目的地区、县分为3类，即先开通区域(太原)，后开通区域(晋西南)和未开通区域.对比各区域出行目的构成情况，如图5所示.

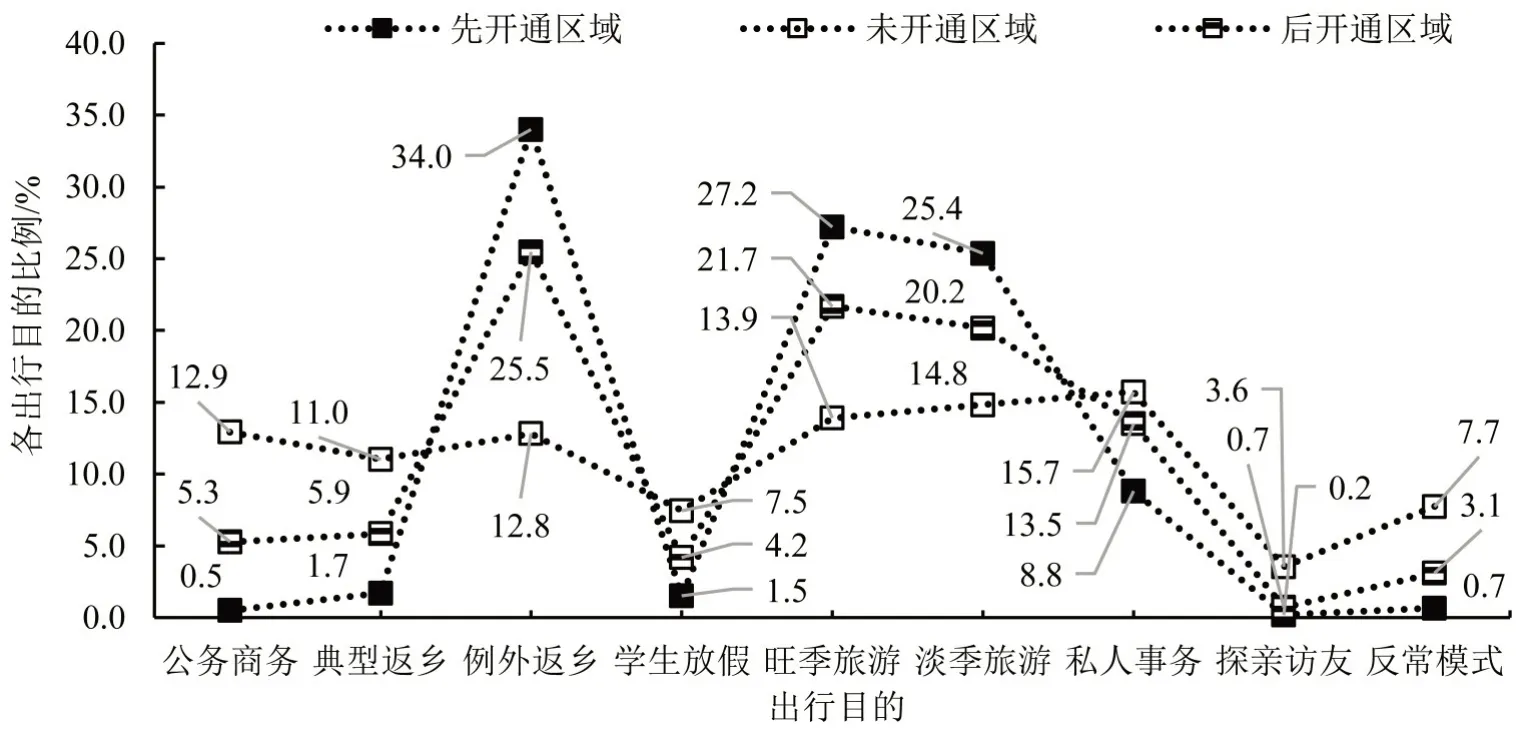
图5 3 类区域出行目的构成对比Fig.5 Comparison of trip purpose configuration in three areas

先开通及后开通区域出行目的构成相似，表现出失衡态势，仅有例外返乡和旺季、淡季旅游这类非强制出行；而未开通区域仍保留多元化出行目的构成，不存在明显占主导的出行目的.

以后开通区域5 个区、县为对象，采用固定效应面板回归模型，研究在高铁开通前(2014年)，高铁开通后(2015—2017年)各目的出行量演化影响因素.列出通过F检验的6 类出行目的分析结果，如表3所示.

表3 固定效应面板回归模型结果Table 3 Result of fixed effects panel regression model

由表3可知，各目的出行量均呈萎缩趋势，但受各因素影响程度不一.其中，例外返乡受高铁开通和轿车保有量增加的抑制作用最为显著，旺季、淡季旅游和私人事务次之，典型返乡和学生放假抑制作用较小；城镇化率的增加有助于提升道路客运团体旅客出行量；国内生产总值(GDP)的影响均不显著.

4 结 论

本文构建嵌入出发时间的主题模型可以在不依赖回访调查前提下推断团体旅客出行目的.模型对于主题标注具有同时考虑特征分布和出发时间分布的优势，对出发时间预测精度为90.9%，证明了模型的有效性；与监督学习方法相比，可以更好地识别私务出行.基于票务数据，模型将50个主题标注为4种常规出行目的，以及无法用既有模型发现和概括，但却不容忽视的非常规类型.案例分析发现，道路客运出行目的构成呈现显著地区差异；面板模型分析表明，高铁开通情况和轿车保有量对6类目的出行量存在负向影响，城镇化率则具有正向影响.