新冠疫情对城市核心区交通安全的干预效应分析

赵 丹，王景升*，周 妍，刘 东，邢立利

(1.中国人民公安大学治安与交通管理学院，北京102163；2.浙江警察学院交通管理系，杭州310053；3.浙江省宁波市交通警察局，浙江宁波315100)

0 引 言

2020年初爆发的新冠疫情对我国城市交通运行产生较大影响.疫情影响下，出行者个体交通方式选择和通勤交通结构发生变化[1]，私人交通与公共交通分担率呈现“一升一降”的趋势[2-3].探讨城市出行结构变化后的交通安全特征，研究疫情对交通安全特征影响的量化分析方法，有助于掌握疫情下交通安全随政策推进而产生的时间变化规律，评估新冠疫情对城市交通的影响.

目前，很多文献对疫情期间的公共交通组织[2]、交通管制[4]，以及病毒通过交通系统传播扩散机理和传染病防疫策略[5-6]等进行研究，针对疫情对城市交通安全影响的研究较少.城市核心区是城市交通需求的“集散地”，大量的通勤交通使其成为反映疫情停工停产、复工复产政策对交通影响的“晴雨表”，探讨疫情影响下非正常交通需求引发的交通安全特性变化有重要意义.本文提出运用机器学习算法和干预模型量化新冠疫情政策对交通事故量影响程度的方法，以浙江省宁波市核心区(东部新城)的交通事故接处警数据，评估新冠疫情对交通安全产生的直接影响.

1 数据收集

1.1 研究区域与数据收集概况

东部新城是宁波市行政与商贸中心所在地，面积12 km2，道路总里程68.4 km.2018年该区域发生路内交通事故8 828起，2019年发生8 776起，平均每日发生事故约24起.本文收集该区域2019年1月1日～2020年5月24日的交通事故接处警数据，得到511 d 交通事故数量，形成时间序列数据.统计2019年的交通事故数量，一是为样本量扩容，二是为滤除节假日、休息日等因素影响，区分由于疫情引起的事故量突变.交通事故量时间序列描述性统计如表1所示.

表1 交通事故量时间序列描述性统计Table 1 Descriptive statistics of traffic accidents sequence

1.2 区域疫情防控概况

据宁波市卫健委统计，2020年1月21日发现首起新冠肺炎病例，2020年2月20日达到最大感染人数157 例，后续无新增病例.根据文献[7]对疫情阶段的区分方法，结合宁波市各项重要政策出台的时间节点，划分疫情阶段如表2所示.疫情爆发初期，对出行密集度高的地区尽早预警；疫情快速传播时期，执行严格社区管控、停工停学、封闭进出城通道和交通禁行等措施，进行交通阻断；疫情持续传播期，疫情增速放缓，城市运行开始启动，交通秩序逐渐恢复阶段，仍需限制不必要的交通需求，进行交通管控；疫情恢复期，居民出行和社会活动大幅增加，公共交通正常运营，仍需警惕疫情反复的风险，视为交通需求疏解期.

表2 2020年宁波市新冠疫情防控重要政策Table 2 Main events during COVID-19 epidemic period in Ningbo,2020

2 疫情影响下的交通事故时间分布特征

以周为单位统计疫情期间交通事故数量.统计期内，除疫情因素外，节假日也是影响交通事故数量的显著因素，日期与节假日对应关系如表3所示，统计期内2年的交通事故分布情况如图1所示.

表3 日期与节假日对应关系Table 3 Relationship between date and calendar day

图1 2019 与2020年1～5月交通事故量同期对比Fig.1 Comparison of number of traffic accidents from January to May in 2019 and 2020

由图1可知：

(1)受疫情影响，2020年周交通事故量在交通阻断期和管控期出现低谷，1月27日起连续3周低于20起，最低值为7起；2019年周事故量最低值出现在春节休假期间，发生事故27起，随后事故数量快速上升至与春节前同一水平，每周约100 起.对比可知，剔除春节假期因素，交通阻断和管控措施使交通事故发生率下降约3/4.

(2)随着复工复产政策出台，交通事故数在2020年2月中旬管控期开始后，以每周翻1倍的速度增长，最终在3月上旬达到稳定，3月以前的事故数量约为2019年同期的30%～40%，随后差异逐渐减小.

(3)2020年3月8日以后，疫情持续期的事故数量比较平稳，未随节假日发生变化，周平均事故量130 起；2019年事故数量则波动较大，周平均事故数量160 起，清明节事故量达到峰值，比平时多1/2，五一劳动节期间事故数量大致相等.

3 疫情影响下交通事故量序列突变分析

时间序列受到外部事件影响后，数据突然与主体呈现变化较大的偏差，且通常会在一段时间内改变时间序列的路径，称为结构突变，其发生的时间称为突变点[8].小波分解能够通过时间和频率的局部变换，区分高频和低频信息，保留序列在各个不同频率段的成分，并且能有效地从观测时间序列中提取真实的变动信息，识别结构突变特征[9].

交通事故量受节假日、疫情因素影响发生变化.本文利用小波分析方法确定事故数的时间序列{yt}(t=1,2,3,…,511)的主要趋势及结构突变点.小波分析参数选择db2(多贝西二阶小波)，分解为3层，得到3组细节分量和3组近似分量.细节分量呈现序列的随机噪声和扰动，近似分量反映信号的主要趋势，故用近似分量识别结构突变点.交通事故原始序列及3 层近似分量a1～a3 小波分解结果如图2所示.

由图2可知：

(1)原始序列有2 个明显的低谷区，对应的分别是2019年、2020年春节和疫情期间；a1,a2 中保留较多的原始序列噪声，从a3 开始，突变趋势变得明显.

(2)近似序列的幅值最低点可视为突变点，a3序列突变点序号为394，对应的时间为2020年1月29日，结合表2和图1可知，当日该区域进、出城交通开始封闭，此突变点处于交通阻断期.

(3)突变点处于春节(2020年1月23日)以后，按照春节休假7 d的规律，2019年交通事故量于春节(2月4日)后一周(2月10日)迅速恢复到节前水平，如图1所示.然而，突变点却呈现出最低谷，据此推断，a3 的突变点394 是剔除春节假日带来的事故量下降影响后的序列突变.

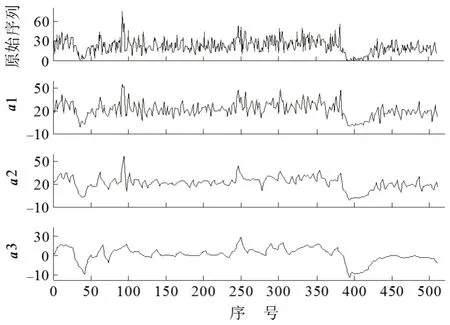
图2 交通事故量序列的小波分解结果Fig.2 Wavelet decomposition of traffic accidents sequence

4 疫情政策对交通事故量的干预效应分析

4.1 干预变量与函数选择

时间序列受到外部政策和事件影响的过程称为干预.干预分析是从定量的角度评估政策或突发事件对时间序列的具体影响[10].干预模型为

式中：yt为t时刻受事件影响的事故时间序列值；Nt为t时刻不受事件影响的时间序列值；f(λ,ξ,t)为干预变量ξ对t时刻时间序列的干预效应；λ为未知参数.

干预变量ξ产生的干预效应Zt为

式中：K为干预变量个数；B为滞后算子；ξtj表示t时刻第j个干预变量；ωj(B)，δj(B)为第j个变量干预程度的未知参数.K=1 表示只有一个干预变量，此时干预效应ωj(B)和δj(B)简化为

式中：B(s)和B(r)分别为s步和r步滞后算子.

按照影响时间的长短，干预变量ξ分为持续性变量和暂时性变量.持续性变量表示事件在T时刻发生后对时间序列产生长期影响，暂时性变量表示事件在T时刻发生后对时间序列的影响是暂时的，分别表示为

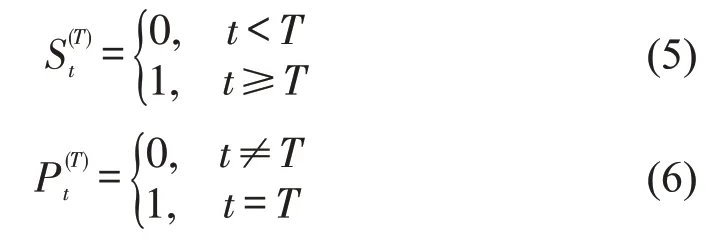
文献[10]给出持续性干预效应的2 种影响形式为

式(7)为干预变量产生的影响Zt突然发生(未滞后)，影响强度为ω，长期持续且不变；式(8)表示影响逐渐开始且长期持续.

4.2 干预模型构建与分析

运用干预分析方法进行新冠疫情影响程度评估的步骤为：首先，利用干预事件发生前的数据构建合适的模型，外推T时刻以后的序列值，视其为不受干预事件影响的序列；其次，计算T时刻后的外推序列值与实际值的残差，得到的残差序列，即为受干预事件影响的具体结果；最后，选择干预函数形式，运用残差序列估计干预模型中的未知参数，得到干预影响.

(1)拟合模型构建.

以a3 为分析序列，将其划分为[1,393](干预前)和[394,511](干预后)2 个阶段，时间段[1,393]作为构建理想趋势外推模型的数据集，包含393组输入变量{yt-1,yt-2,yt-3,yt-4}(5≤t＜393)及其对应的输出变量{yt}(5≤t≤393)，训练集和检验集从样本中随机选择，比例为60%和40%.为增加预测准确性，构建广义线性模型和支持向量机模型对数据进行拟合.

广义线性模型设事故量{yt} 为服从指数分布的因变量，{yt-1,yt-2,yt-3,yt-4} 为自变量，由于该模型不要求因变量必须符合某种分布(例如：正态分布、二项分布、泊松分布等)，故灵活性和精度更高.支持向量机回归模型的原理是给定一组由输入变量{yt-1,yt-2,yt-3,yt-4} 和输出变量{yt} 构成的数据集，并找到一个模型g(yt-1,yt-2,yt-3,yt-4)，使g(yt-1,yt-2,yt-3,yt-4)的模型输出值{Nt} 与实际值{yt} 尽可能接近.

对2 个模型进行训练和参数标定.其中，支持向量机回归(SVR)模型采用高斯核函数(RBF)，核函数参数取0.005，惩罚系数取1 000，将数据集分成10 份，每次9 份数据用于训练，1 份数据用于测试，最终选择10 次计算结果中误差平均值最小的一组参数作为最优参数.2种模型检验集数据的误差分析结果如表4所示.

表4 2 种模型拟合精度评价Table 4 Fitting precision evaluation of two models

由表4可知，SVR 模型预测误差更低，平均绝对误差为0.290.

将2个模型得到的预测值与真实值进行对比，通过查看散点在多大程度上靠近对角线来衡量拟合优度，如图3和图4所示.

图3 广义线性模型拟合优度Fig.3 Goodness of fit of generalized linear model

图4 支持向量机回归模型拟合优度Fig.4 Goodness of fit of support vector machine regression model

图3和图4中拟合优度R2值说明，SVR 模型预测值与实际值的差异更小.SVR 模型对{yt} (1≤t≤393)的拟合结果如图5所示，可以看出，拟合结果很理想.

图5 a3 序列[1,393]拟合图Fig.5 Fittig diagram of series a3 from 1 to 393

(2)干预后事故量预测.

利用已训练好的支持向量机模型，对突变点后的时间序列值进行趋势外推.例如，对于突变点394，输入{y393,y392,y391,y390}，模型输出值记为N394；对于点位395，输入{N394,y393,y392,y391}，输出N395.依次外推，得到一组预测值{Nt}(394≤t≤511)，视为不受疫情政策影响的序列.{yt} 与{Nt} 之差，即为疫情影响结果，记为{Zt}.图6给出SVR 模型预测值和实际值的对比及干预值曲线.

图6 a3 序列[394,511]预测结果Fig.6 Prediction of series a3 from 394 to 511

由图6可知：

①突变点所处的交通阻断期事故量远低于不受疫情影响时的事故量，变化趋势与实际值有极大偏离，在[394,423]阶段甚至呈现相反趋势，干预效应先增强后减弱.

②在424点位(对应2020年2月28日，省际客运恢复通车)以后，事故量的差异显著减小并稳定在15 起以内，预测结果与图1所呈现的2020年3月以后周事故量受疫情影响比2019年同期低的趋势相吻合，且干预效应基本稳定.

(3)干预模型估计.

如前所述，a3 拟合模型预测值与实际值的残差为疫情政策的干预效应.由图6可知，残差序列{Zt} (3 94≤t≤511)代表干预变量的影响程度和作用区间.考虑干预影响先增强后减弱，最后趋于稳定的特性，干预函数应为分段形式，即

估计式(9)中参数，根据干预值曲线确定，当394≤t≤423 时，r=2；利用回归模型的参数估计方法，得到ω1=-12.230，δ1=0.687，δ2=-0.309，R2值为0.883.各系数的含义为：新冠疫情初期管控政策产生影响使交通事故量平均每日下降12.23起，前期以68.7%的速度衰减，后期又以30.9%的速度回升.Zt=表示疫情产生影响强度为定值，取{Zt}序列在[424,511]区间的平均值，得到ω2=-11.707，表示疫情常态化防控下，相对宽松的管控政策对交通安全的影响长期持续，且稳定地使事故量平均每日下降11.707起.

5 结 论

本文提出运用小波分析技术、支持向量机模型和干预模型量化新冠疫情政策对交通事故量影响程度的方法，并以宁波市核心区为例进行验证计算.

(1)基于统计方法分析疫情期间交通事故量的变化特征，发现疫情管控措施使交通事故发生率下降约3/4；随着复工复产政策的实施，事故量回升，且不受节假日因素影响.

(2)运用小波分解技术识别出交通事故量序列突变点，该突变点位于2020年春节后一周，说明算法主动剔除了春节假日因素对事故量的影响，证实疫情导致事故量下降在春节后体现的更为明显.

(3)针对存在突变点的小波分解近似分量，在支持向量机预测基础上，构建分析疫情影响程度的干预模型，发现干预效应具有阶段性，先增强后减弱，最终稳定，与不同疫情阶段采取不同交通管理对策是符合的.

(4)疫情政策的影响使事故量平均每日下降12.23 起，初期以68.7%的速度衰减，再以30.9%的速率回升；随着复工复产政策的实施，进入交通需求疏解期，疫情常态化防控政策稳定地使交通事故量平均每日下降11.71起.