基于互相关算法的两种燃气管线泄漏定位方法比较

上海煤气第一管线工程有限公司 王敬凡

近年来，天然气运输管网泄漏问题导致爆燃事故频发，对国民经济和居民生命财产安全造成严重危害，泄漏源的定位问题逐渐引起各界重视。其中，连续焊接钢管阀门泄漏问题最具代表性，亟待实现泄漏源的精确定位。

1 声发射技术概述

声发射技术(Acoustic Emission，AE)是一种动态无损检测技术。由于其原理简单，测量结果精度高，具有动态性、整体性和高效性等特点，在管道监测领域得到了广泛的应用。当管道发生泄漏时，气体在泄漏点处向外喷射，引起管壁振动而产生应力波，形成声发射信号，利用传感器捕捉该信号并进行分析，可以进行管道泄漏的预警和定位。

实现泄漏源定位的关键在于得到准确的信号时延估计。互相关算法作为一种经典的时延估计法，运算简单，原理明晰，被大部分研究所采用。但是由于采集到的声发射信号往往夹杂大量噪声，并伴随着信号的频散和衰减，呈现出非平稳的特性，利用直接互相关技术不能得到较好的定位结果，因此需要对原始声发射信号进行降噪处理，从而提高定位精度。小波分解(Wavelet Transform，WT)和经验模态分解(Empirical Mode Decomposition，EMD)是两种近年来应用较为广泛的非平稳信号处理方法。

小波分解WT可以在时频域上表征信号的局部特性，在低频部分具有较高的频率分辨率，在高频部分具有较高的时间分辨率，能够很好地去除噪声。吴志敏等人[1]采用基于小波分解的互相关定位法，对不同压力条件下的实验室管道泄漏工况进行定位实验，得到的定位结果精度达到 95%以上。Mostafapour A等人[2]以埋地燃气管道为对象，模拟孔漏进行泄漏定位实验，利用小波分解进行去噪处理，同样得到了较好的定位结果。Davoodi S等人[3]模拟孔漏，通过改变泄漏孔径，对实验室管道进行多次实验，定位精度达到96%以上。

由于 WT中小波基的选择会直接影响定位精度，且频域划分层数、尺度均需人为确定，不具备自适应的特点，因此经验模态分解EMD作为一种自适应分频分析法，逐渐得以应用。谷小红等人[4]将EMD用于埋地水管的泄漏定位，该水管约20 m长，最终定位误差仅0.2 m。孙立瑛等人[5]对1根长约16 m的气体管道进行泄漏实验，EMD分析的定位结果误差为6.3%，此外，孙立瑛等人[6]还对1根长24.5 m、管径154 mm的普通低碳钢管进行气体泄漏实验，EMD得到的平均定位误差仅为5.34%。Cui X等人[7]对1根6 m长的不锈钢铁管进行CO2气体泄漏实验，结果表明定位误差在 1%以内。郭晨城等人[8]提出，在利用 EMD分解重构信号时，以各个分量和原始信号的互相关程度大小为依据，挑选合适分量，以进一步提高结果精度。EMD虽然可以自适应地实现信号的多分辨率分析，但分解结果往往会出现模态混叠问题。

对于燃气管道泄漏定位问题，基于WT的互相关定位法和基于EMD的互相关定位法均有较好的应用前景，但仍需要一定的工作来验证二者对实际泄漏定位的适用性。因此，本文以连续焊接钢管燃气管道的阀门泄漏为实验对象，分别采用WT法和EMD法进行降噪处理，同时进行泄漏定位，并对比了定位结果。

2 基于声发射技术的泄漏定位原理

如图1所示，在泄漏源两侧布置声发射传感器，当泄漏发生时，声发射信号将沿着管道分别向两侧传播。由于传播距离不同，所以两侧传感器接收到的信号将存在时间差。将信号时间差(信号时延)与两传感器的间距、声发射信号传播速度相结合，即可求算泄漏点的位置。

图1 互相关定位原理示意

信号时延可以采用互相关法获得。但由于管道运行环境中干扰较大，直接采用互相关法往往不能得到准确的时延，因此常常首先采用WT降噪法和EMD降噪法对信号进行处理。

2.1 WT降噪法

由于声发射信号包含大量噪声，泄漏信号仅存在于部分频带中，为了提高互相关定位的精度，采用WT法对信号进行变换，提取特定频带信号处理，在此基础上实现定位。WT法的本质在于将信号用一组小波基函数进行重构。

基于WT的互相关定位主要步骤如下：

(1)分析原始信号的频谱特征，判断泄漏信号特征频段。

(2)根据信号频谱特征确定分解层数，选定小波基函数。

(3)对 2个传感器的信号进行小波分解，选取与泄漏信号主频段匹配的分量进行信号重构。

2.2 EMD降噪法

EMD得到的分量称为本征模态函数(Intrinsic Mode Function，IMF)，IMF应该满足条件：该函数的极值点(极大值或极小值)数目和过零点数目相等或最多相差一个；由局部极大值构成的上包络线与由局部极小值构成的下包络线的平均值为零。具体计算流程为：

(1)用三次样条函数拟合出原信号x(n)的上、下包络线，其均值为m1；由h(n)=x(n)－m1，得到新序列h(n)。

(2)若h(n)满足IMF函数的要求，即为第一个分量IMF1；若不满足，则令h(n)作为新的信号x，重复以上操作，直到得到满足要求的IMF1。

(3)定义新的数据列r1(n)=x(n)－h1(n)，把r1(n)看作新的信号x，重复步骤(1)和(2)得到第二个分量IMF2。

(4)循环步骤(3)，直到最后一个数据序列r(n)不能被继续分解，即达到设定的阈值或者变成单调函数。

(5)观察频谱并挑选主频和泄漏信号主频相对应的IMF分量，重构信号。

3 连续焊接钢管泄漏实验

为了验证上述算法的适用性并探究法兰接头对定位的影响，以连续焊接钢管的阀门泄漏事件为对象，针对某一桥管设计实验。实验布置和现场实际情况如图2所示。

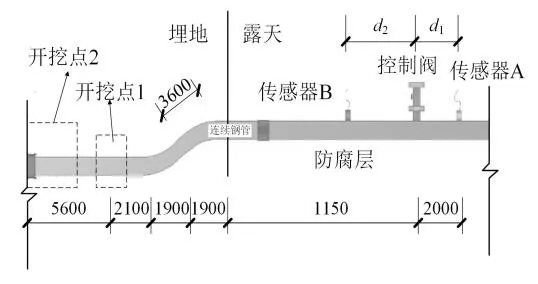
图2 燃气桥管泄漏定位试验布置

实验管道由露天段和埋地段两部分组成。左端通过斜管埋入土中，右端露天。实验主要在露天段进行，露天段全长14 m左右。令露天段中部的控制阀作为本次实验的泄漏源，拧动阀门使小漏发生，产生声发射信号。采用2个AE传感器，传感器A和控制阀之间的距离为d1，传感器B和控制阀的距离为d2。露天段管道上还存在一处法兰，用以探究法兰接头对定位的影响。AE传感器用胶带固定在管壁上。设计实验工况如表1所示，工况1～6的信号仅通过直管，工况7的信号经过法兰接头。

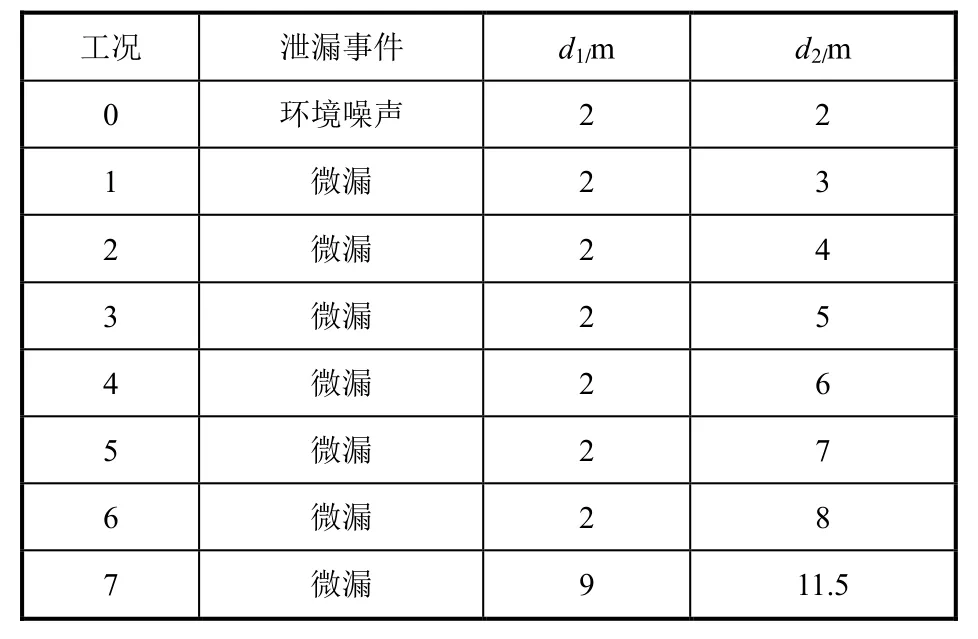
表1 定位实验工况

每个工况均连续采集5组数据，每组数据时长1 s，包含106个样本点。后续分析时，将每组数据划分为样本长度为16 384(时长16.384 ms)的小样本进行处理。

4 定位结果与对比

采集到的各工况声发射信号分别利用 WT和EMD进行降噪处理，并进行泄漏源定位，将二者结果进行比较，取声发射信号波速为2 000 m/s。

采用精度α衡量两种降噪方法的定位结果的优劣，其计算式如式(1)所示:

式中：α——定位精度，m；

d1——传感器A和泄漏源的实际距离，m；

Y1——计算得到的传感器 A与泄漏源的距离，m；

D——两传感器之间的距离，m。

4.1 WT降噪法的泄漏定位结果

由初步分析可得，连续焊接钢管泄漏信号在40～50 kHz的范围内存在峰值，因此取该频段信号作为主要分析对象。结合本实验信号的频域特征，根据WT的原理，选用db6小波，对信号进行5层小波分解，得到 6个频带的分解信号，分别为：A5(0，15.625 kHz)，D5(15.625 kHz，31.25 kHz)，D4(31.25 kHz，62.5 kHz)，D3(62.5 kHz，125 kHz)，D2(125 kHz，250 kHz)，D1(250 kHz，500 kHz)。其中D4层信号包含了泄漏信号的主频部分，对其进行小波重构得到新的信号，在此基础上进行互相关定位。定位结果如表2所示。

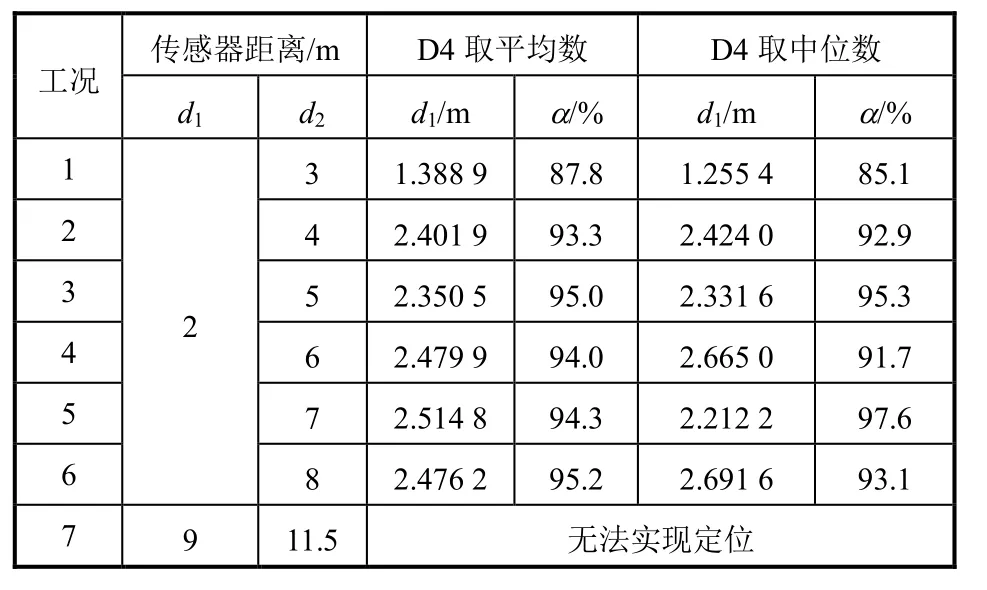
表2 基于小波分解的互相关定位结果精度表

对于泄漏信号仅在直管段传播的工况 1～6，本方法取得了较好的结果，大部分工况的定位精度均在92%以上。由此可见随着信号传播距离的增大，仍然可以得到很好的定位结果，但对于经过法兰的工况7，无法得到有实际意义的定位结果。

4.2 EMD降噪的泄漏定位结果

采用EMD对工况1～7的信号进行分解，为了尽可能详细地获取低频分量，分解层数定为12层。由于信号中噪声能量水平比较高，所以按照能量权重选取分量重构信号的方法不可取，因此分别做出各个分量的频谱图，选取主频位于40 kHz左右的分量进行重构。通过对各个频谱图观察可知，只有分量IMF3和IMF4在40 kHz左右存在峰值，因此以其为重构对象进行分析，见图3。

图3 工况4频域

通过试算，对传感器A采集到的信号，取IMF3代替原信号，对传感器B采集到的信号，取IMF3和IMF4的和重构信号，此时二者的互相关定位结果最好，因此将这种重构方法用I3-34表示。具体的定位精度如表3所示。

表3 基于EMD的互相关定位结果精度

从表3可知，当信号仅过直管时，基于 EMD的互相关定位法可以得到满足实际工程需要的定位结果，传播距离的变化对定位影响不大，但是，对于信号过法兰的情况，EMD同样无法实现定位。

4.3 定位结果对比

不论是WT还是EMD，均可以有效地实现直管泄漏信号降噪，大大提高泄漏源定位精度。对于存在法兰的工况，二者都不能得到令人满意的结果。经过法兰后的泄漏信号在40 kHz的峰值消失，说明法兰将泄漏信号完全衰减，因而无法实现定位。

为了进一步比较两种方法，本文从总体精度和标准差两个方面进行评价，具体结果如表4所示。

表4 定位方法对比表 %

对于四种对比方式，基于小波分解的D4层取平均数定位法的总体精度较高，具有更好的准确性，而基于EMD的I3-34取中位数定位法的标准差较小，具有更好的稳定性。

5 结语

本文研究了连续焊接钢管阀门泄漏定位问题，依据现场实验数据，探究了泄漏的声发射信号特征，并对基于WT降噪的和基于EMD降噪的互相关泄漏定位方法进行了研究和对比，得到了以下结论：

(1)连续焊接钢管阀门泄漏信号在40 kHz左右有一个频域峰值，在经过法兰后该峰值消失。

(2)基于 WT的互相关定位法可以很好地解决直管段的泄漏定位问题，选用平均数的结果显示了更高的准确性和稳定性，各工况定位精度在90%左右，部分工况可达95%以上。

(3)基于 EMD的互相关定位法也能得到不错的定位结果，采用I3-34定位时，各工况定位精度达到90%左右，部分工况精度可达95%以上。

(4)法兰能使得泄漏信号的峰值衰减消失，因而两种降噪方法均不能有效定位。