薄板烘丝机出口水分预测模型研究
陈 伟,朱星宇,左 雯
(红云红河烟草(集团)有限责任公司,云南 弥勒 652399)
1 研究背景
在烟草制丝加工过程中,薄板烘丝机出口水分值不仅是烘丝机的重要工艺参数,也对后续工序加工的产品质量的优劣有着不可忽视的作用。在正常的生产过程中,烘丝机受入口烟丝流量、水分等多种因素影响,常常出现出口水分波动,超出工艺指标要求,对烟草产品的品质产生不利影响。
目前对烟叶生产线上所用烘丝机的研究较多,有的对烟丝在烘丝机内的运行状态进行分析并提出了烟丝滞留时间模型[1,2];有的通过数据挖掘,对烘丝机出口水分相关的重要性关系进行分析研究[3]。也有从烘丝机原理出发,对烘丝机的数学模型进行研究探讨,总结出烘丝机热学方程以及烟丝在烘丝机内运行的数学模型[4-6],但由于其中部分参数与烘丝机自身特性密切相关,难于通过热学方程、运动方程计算出出口水分实际值,仅具有参考价值,难以应用于实际控制中。
本文研究旨在通过可行的数据挖掘处理方法,分析确定烘丝机出口水分与各工艺参数的关系,得出出口水分与薄板烘丝机相关联的过程数据之间的数学表达式,从而实现出口水分的预测,以提高出口水分控制的稳定性。
2 相关因素确定
2.1 薄板烘丝机工艺介绍
叶丝线的工艺流程如图1所示。

图1 叶丝处理工艺布局
我们为建立烘丝机的出口水分模型,需要考虑这些仪器的安装位置和烟丝的流动情况,确保检测值对应流动中的同一部分烟丝,烘丝机出口水分模型才有实际意义。
2.2 薄板烘丝机出口水分影响因素
根据薄板烘丝机结构原理和控制原理,以及生产操作的实际经验,可以大致确定影响烘丝出口水分的因素主要有:
(1)烘丝机出口水分设定:该设定值之间影响烘丝机薄板温度控制。
(2)来料水分:其他条件保持恒定,出口烟丝水分和入口烟丝水分呈正比例关系。
(3)进料烟丝流量:其他条件保持恒定,烘丝机入口烟丝流量越大,烘丝机出口烟丝水分越大。
(4)烘丝机热风温度:其他条件保持恒定,烘丝机热风温度越低,出口烟丝的水分越高,反之则越低。
(5)筒壁温度:烘丝机筒壁温度即为薄板温度,薄板温度越高,叶丝里面的水分蒸发的越多,出口烟丝的水分越低。
(6)薄板转速,薄板转速越快,烟丝滞留时间越短,出口水分越大。
(7)薄板烘丝机的热风风门角执行器开度实际值:该风门开度影响到进入薄板内部的热风量,也会影响到烟丝烘干效果。
(8)薄板烘丝机的排潮风门角执行器开度实际值:该风门开度影响薄板内部循环风量,也对烟丝水分散失有影响。基于之前研究结论显示[7],上述各因素中,叶丝流量、入口水分、热风温度、筒壁温度是影响薄板烘丝机出口水分的重要因素。
2.3 相关因素数据分析
2.3.1 数据获取
INSQL提供了OLEDB接口,可以通过该接口进行类似数据库的查询操作。为了实现分批次、分牌号按所选定的过程变量进行查询,我们用VB开发了一个数据导出软件。为了保证数据量,我们分别选择了各个牌号的10多个批次进行导出。我们提取了如下可能影响到烘丝机出口水分的因素,并从实时数据库里面提取出来进行分析。
CA6水份检测,CA3水份检测,CK2电子秤瞬时流量,SH1薄板烘丝机烘筒温度实际值,SH1出口水份设定,SH1热风温度实际值,SH1热风风门角执行器开度,SH1排潮风门角执行器开度。
2.3.2 原始数据处理
从设备位置图1可以看出,电子秤CK2和水分仪CA3在烘丝机之前,水分仪CA6在烘丝机出口之后的振槽上,烟丝通过这些点的时间是不同的。那么采样上来的这些点的过程数据也没有对应同一部分烟丝,这就需要对采样值进行时间对齐。经过实际测量,可以得到烟丝从CK2和CA3位置流动到烘丝机入口位置所需时间t1,同样也可以测量烟丝从烘丝机入口到水分仪CA6处的时间t2,那么以烘丝机入口位置为时间基点,CK2、CA3的值需要提前t1,CA6的值需要延后t2,从INSQL导出的原始数据采样时间间隔为5秒,这就可以确定各个原始数据正确位置。

表1 出口水分与各过程值之间的相关系数r及相关性

表2 生产状态多元回归结果
2.3.3 数据验证
我们假设烘丝机出口水分(CA6检测值)为y,入口水分(CA3检测值)为x1,CK2电子秤瞬时流量为x2,SH1薄板烘丝机烘筒温度实际值为x3,SH1出口水份设定为x4,SH1热风温度实际值为x5,SH1热风风门角执行器开度为x6,SH1排潮风门角执行器开度为x7。
我们通过MATLAB对原始数据进行检查,以判断是否符合正态分布。首先从EXCEL表内读出每个数据系列,然后进行T测试。

图2 热风温度频次图和正态概率图
如图2所示,热风温度服从正态分布。经过检验,各因素都服从正态分布。
2.3.4 相关性检查
为了检查各过程值与出口水分是否存在相关性,我们计算各过程值与实际水分的皮尔逊相关系数r来检查。
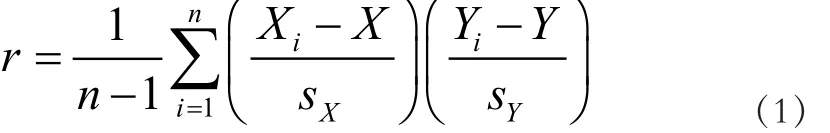
相关系数r的值范围:-1≤r≤+1。其性质有:
当r>0时,表示过程值与实际水分成正相关,r<0时,过程值与实际水分成负相关。
当|r|=1时,过程值与实际水分是完全的线性关系,也就是函数关系。
当r=0时,表示过程值与实际水分之间没有线性关系。
当0<|r|<1时,表示过程值与实际水分之间有一定程度的线性相关性,如果|r|越趋近于1,则它们之间的线性关系越显著;|r|越趋近于0,则表示它们之间的线性相关关系越不显著。
安照上述公式,使用MATLAB计算出烘丝机出口水分值与烘丝机状态过程值之间的相关系数r如表1所示,并据此作出相关性判断。
3 回归分析模型确立
3.1 多元回归分析
从表1可以看出,烘丝机的三个状态时,出口水分都与烘丝机相关的一些过程变量成线性相关,因此可以考虑用线性回归来进行拟合。而烘丝机处于三个状态时又表现出与各过程值的相关性不同,因此我们把数据按烘丝机状态进行拆分后分段进行拟合,并假设出口水分与各因素之前成线性关系:

式中:y——出口水分实际值;b1,b2,…,b8——线性方程的系数;x1,x2,…,x7——CA3入口水分、CK2电子秤流量、…、SH1排潮风门角执行器开度。
我们使用MATLAB的多元线性回归功能进行拟合,在进行显著性水平为0.05的拟合后,结果如表2所示。
从两个表里的数据可以看出,判定系数R2>=0.6,F远大于临界值,P<0.001,可以判定拟合是有效的。根据MATLAB拟合得到的系数,代入公式(3-1)得到如下各状态时的薄板烘丝机出口水分与各相关过程值之间的数学表达式:

3.2 拟合效果评价
取80%数据样本进行MATLAB模型参数识别,建立烘丝出口水分的预测模型,再将剩下的20%数据代入得到的预测模型公式进行效果验证。生产工艺标准规定实际含水率与设定值的偏差绝对值在5%内判定为合格,所以出口含水率预测值与实际过程值误差在±0.3%内可以判定为预测是成功的。据此如果进行n次预测检验,第i次的预测值为,实际值为,定义预测误差和准确预测比例如下:

多元回归拟合的结果如下:生产状态时可决系数R2为0.4242,预测误差为0.0925,工艺要求的误差范围是0.5%,这个误差是在允许范围内,预测的准确率也较高,准确预测比例Ra达到96.73%。在烘丝机的操作中,主要就是控制生产状态时候水分。在整个完整批次的生产过程中,生产状态持续的时间也最长。因此生产状态使用线性回归的方法得到的数学模型进行预测是可行的,也能满足精度要求。

图3 模型预测水分与水分比较
图3 中,蓝色为模型预测水分,红色为实际水分,可以看出,蓝线在时间上领先红线一些,而蓝线的波动趋势基本与红线相同,说明预测模型比较准确。
4 总结
本文通过多元线性回归方法的模型误差、预测准确率等的计算,得出使用这种方式建立的模型在烘丝机生产状态时都有较高预测准确率,可以把得到的数学模型进行实际应用的结论。

