波形钢腹板支架结构的稳定承载力研究
王卫强
(甘肃博睿交通重型装备制造有限公司,甘肃 兰州 730000)
波形钢腹板以其腹板抗裂性能强和结构自重轻等优点在PC组合箱梁桥钢腹板中脱颖而出,受到广泛应用。在我国,结合吴丽丽等人提出的煤矿巷道直墙半圆拱形波形钢腹板支架稳定承载性能研究,通过大量试验表明波形钢腹板支架结构的屈曲应力及屈曲模态,取得了一定的研究成果[1]。明确了波形钢腹板支架结构整体稳定性的主要影响因素包括:纵向残余应力——纵向残余应力使波形钢腹板支架结构刚度降低,也降低稳定承载力;初弯曲——由于残余应力的存在,初弯曲使截面更早进入塑性,降低稳定承载力;初偏心——初偏心对稳定承载力的影响本质上同初弯曲;杆端约束——杆端约束越强(如固定),承载力会越高;构件几何长度——短柱通常产生强度破坏,长柱、中长柱产生失稳破坏;波形钢腹板支架结构截面几何特征——截面回转半径增大,稳定承载能力提高。而国外针对波形钢腹板支架结构的稳定性能方面研究起步较早,早于20 世纪初,Bergmann 就通过弹性稳定理论得出波形钢腹板支架结构的剪切屈曲承载力的计算公式。根据国内外试验资料,提出波形钢腹板支架结构的稳定承载力研究[2]。
1 波形钢腹板支架结构的稳定承载力研究
波形钢腹板支架结构的稳定承载力主要取决于支架结构的塑性转动量,支架结构的塑性转动量与截面相对受压区高度有关[3]。基于此,在本文进行的波形钢腹板支架结构的稳定承载力研究中,通过三步骤进行重点研究。
1.1 计算波形钢腹板弹性范围屈曲
由于波形钢腹板会在外力作用下导致屈曲承载力降低,因此,波形钢腹板弹性范围必然会造成一定程度上的屈曲。波形钢腹板弹性范围屈曲示意图,如图1 所示。
根据图1 所示,本文结合Bergmann 提出的波形钢腹板支架结构的剪切屈曲承载力的计算公式,计算波形钢腹板弹性范围屈曲[4]。设波形钢腹板弹性范围屈曲为τ ,则其计算公式,如公式(1)所示。
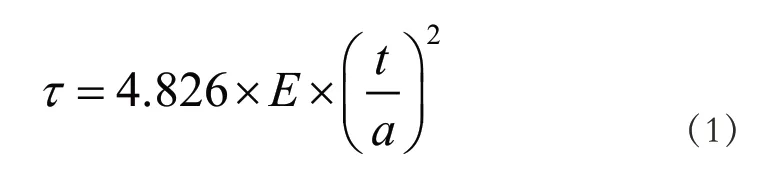
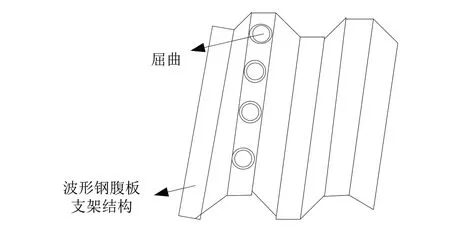
图1 波形钢腹板弹性范围屈曲示意图

图2 波形钢腹板支架结构有限元模型
在公式(1)中,E 指的是波形钢腹板支架结构的弹性模量;t 指的是波形钢腹板的平板段长度,单位为cm ;a 指的是波形钢腹板的厚度,单位为cm。通过公式(1)可以得出波形钢腹板弹性范围屈曲,为规范支架结构中屈曲临界应力提供基础数据。
1.2 规范支架结构中屈曲临界应力
考虑到波形钢腹板支架结构的稳定承载力主要是由腹板承担,规范支架结构中屈曲临界应力是波形钢腹板支架结构稳定承载力的约束条件。计算设支架结构中屈曲临界应力为σ ,则其计算公式,如公式(2)所示。
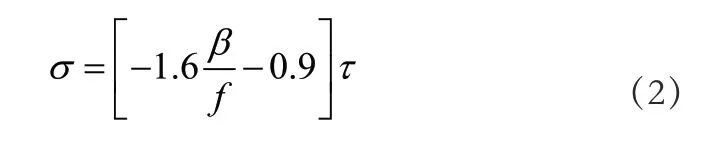
在公式(2)中,β 指的是波形钢腹板支架结构所能承受的最大拉应力;f 指的是波形钢腹板支架结构中的屈服系数。根据多次计算,设波形钢腹板支架结构的抗拉强度为 cf ,通常情况下为支架结构中屈曲临界应力的10.5%~12.2%。因此,可以将波形钢腹板支架结构受弯的屈曲临界应力规范为
1.3 得到波形钢腹板支架结构的稳定承载力
在规范波形钢腹板支架结构中屈曲临界应力的基础上,本文通过构建波形钢腹板支架结构有限元模型,得到波形钢腹板支架结构的稳定承载力[5-7]。波形钢腹板支架结构有限元模型,如图2 所示。
根据图2 所示,将波形钢腹板支架结构在应变值下的稳定承载力代入静力平衡条件可得,波形钢腹板支架结构的稳定承载力计算公式M ,如公式(3)所示。

在公式(3)中,b 指的是波形钢腹板的泊松比;y 指的是波形钢腹板支架结构纵向受力强度等级;x 指的是波形钢腹板支架结构横向受力强度等级;z 指的是波形钢腹板支架结构有限元承载力;n 指的是波形钢腹板支架结构嵌固系数,为实数,通常情况下取值为1.0。
通过波形钢腹板支架结构的稳定承载力计算公式中的自变量可以得出波形钢腹板支架结构稳定承载力的主要影响因素主要包括以上各项参数。整个计算过程均是以波形钢腹板支架结构平截面的假定作为基础,也就是说波形钢腹板支架结构截面各点应变与中和轴的距离必须为正比例。应变与外围相应处的应变一致,在纵向波形钢腹板支架结构受力达到屈服强度之前,截面的平均应变应该达到瞬间的平衡,以符合波形钢腹板支架结构的稳定承载力的要求。
2 结束语
考虑到波形钢腹板支架结构的稳定承载力能够直接影响波形钢腹板支架结构的稳定性,通过以上研究,希望能够为提高波形钢腹板支架结构稳定性提供一定的参考意见。因此,本文进行的稳定承载力研究是十分必要的,且具有现实意义。但本文唯一不足之处在于,没有对波形钢腹板支架结构的稳定承载力通过实例的方式进行深入分析,相信这一点,可以作为波形钢腹板支架结构优化设计领域日后的研究内容之一。

