基于电弧信息时频特征的多层多道焊缝熔宽预测研究

袁飞 岳晨凯 黄勇 李晓鹏 王克鸿

摘要：以多层多道的熔化极气体保护电弧焊接过程为研究对象，以识别熔宽为目标，设置了不同的工艺实验，获得了不同熔宽下对应的电弧信号。对不同工艺条件下的电信号进行了时频特征分析，并利用变分模态分解（VMD）方法提取其时频特征值，结合支持向量机（SVM）模式识别算法对熔宽进行多分类，构建了不同工艺参数与熔宽的预测模型。经验证，预测精度达到98.611 1%。为焊接过程信息化和智能化发展奠定了较好的技术基础。

关键词：电弧;电信号;时频特征;熔宽;预测

中图分类号：TG444+.72      文献标志码：A      文章编号：1001-2003（2021）12-0016-08

DOI：10.7512/j.issn.1001-2303.2021.12.04

0    前言

电弧作为应用广泛的焊接热源，涉及大量的热、力、声等物理特征信息，这些信息体现了电弧的动态行为特征，反映了焊缝成形特征[1]。研究不同工艺参数下的电信号特征，建立电信号特征与焊缝成形特征的关系，对于实现高精度、高灵敏的焊接质量闭环控制具有重要意义。

检测中采集到的信号不经过处理很难辨别其特征。时频分析方法结合了信号在时间域和频率域的特征信息，直观地描述了信号的频率随时间变化的关系，较传统信号统计学分析方法具有巨大优势。近年来，新型自适应时频分析方法——变分模态分解（Variational Mode Decomposition，VMD）的出现为复杂的信号提供了精确的处理手段[2-6]。湖南大学李梦君将VMD方法应用在碰撞信号的去噪上，效果明显优于经验模态分解（Empirical Mode Decomposition，EMD）方法。南京理工大学周晓晓等人[7]利用VMD分解铝合金双丝PMIG（Pulse Metal Inert Gas）焊接电弧等效电阻，计算分解分量奇异谱熵，以等效电阻VDM-奇异谱熵为特征评价铝合金双丝 PMIG焊焊接过程稳定性。湘潭大学罗争光[8]引入VMD方法对磁控埋弧焊自动跟踪信号进行分析处理，结果表明VMD方法提取跟踪信号波形效果明显，提取结果可用于焊缝跟踪精度检测。长春工业大学范高铭[9]结合VMD方法和希尔伯特-黄变换（Hilbert-Huang Transform，HHT）处理焊接钢板振动特性参数，将时频谱的能量-时频分布特征值作为检测焊接钢板残余应力的判别指标。

目前，基于电弧信息时频特征的信号处理已经在单道焊接中得到应用，但大厚板多层多道焊接工况较单道焊接复杂，特别是多重堆积过程中电信号所表现的特征、层间电信号的差异性、电信号与多重堆积效应下焊接质量的关系还有待深入研究。因此，文中基于焊接电信号检测基础，根据多层多道焊接过程中的多重堆积、多重热累积特点，开展了多重堆积下焊接电信号检测分析研究。

1 试验系统及数据采集

试验设备主要为Fronius公司CMT 4000系列焊机、ABB焊接机器人，及送丝、送气系统等。焊接电源设有外控接口，可由RCU 5000i遥控器输出信号调控工艺参数。焊机采用一元化模式焊接，通过调节送丝速度改变电流、电压，得到4组不同层高、层宽的多层多道焊缝，焊接工艺参数如表1所示。

在熔化极气体保护焊过程中，通过对应传感器采集电流和电压信号，经过电路转换，利用USB-4711A数据采集卡的A/D功能将采集到的模拟信号轉换成计算机可识别的数字信号。数据卡采集模块再将电弧电流和电压信号以波形图的形式显示在电脑屏幕上，并保存数据。

2 结果与讨论

2.1 气体金属电弧（GMA）信息的时频特征分析

针对每道焊缝，实时采集焊接电流和电弧电压信号，并将数据存储为文本格式，以便后续利用VMD进行分解分析。在VMD分解中，经过多次试验，对比分析结果，最后模态个数k取8，惩罚因子 α取5 000，以提高分解效率。将采集到的数据文本导入VMD程序中，对其进行均值滤波，并对分解信号进行傅里叶变换和希尔伯特变换，分别得到分解信号的频谱图（FFT谱）和时频谱图（HHT谱），取分解信号的峰值频率为特征值进行后续分析。

以送丝速度为5.5 m/min时的工况为例，分析不同工艺参数下的电流、电压波形。取第5层焊道中间5 000个电流与电压信号数据进行分析，采样频率fs=10 kHz，采样时间t∈[0，0.5]。

2.1.1 电流信号的分解

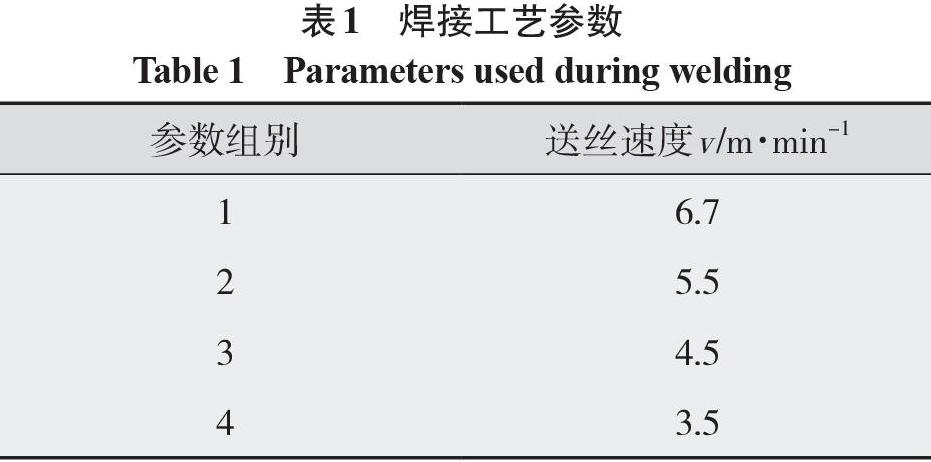
电弧电流分解具体波形如图1～图3所示。图1为实测电流信号及其分解HHT谱，图1a为电流信号的时域图，峰值电流约为270 A，谷值电流约为40 A，且因飞溅有少量缺失。图1b为实测电流信号VMD分解分量经希尔伯特转变得到焊接信号的时频谱图，本征模态分量IMFs对应的频率有7个，由于模态数k=8，说明还有一个残余分量。并且频率越低，HHT谱中的线越平滑，说明焊接电流信号的频率主要集中在低频区域。

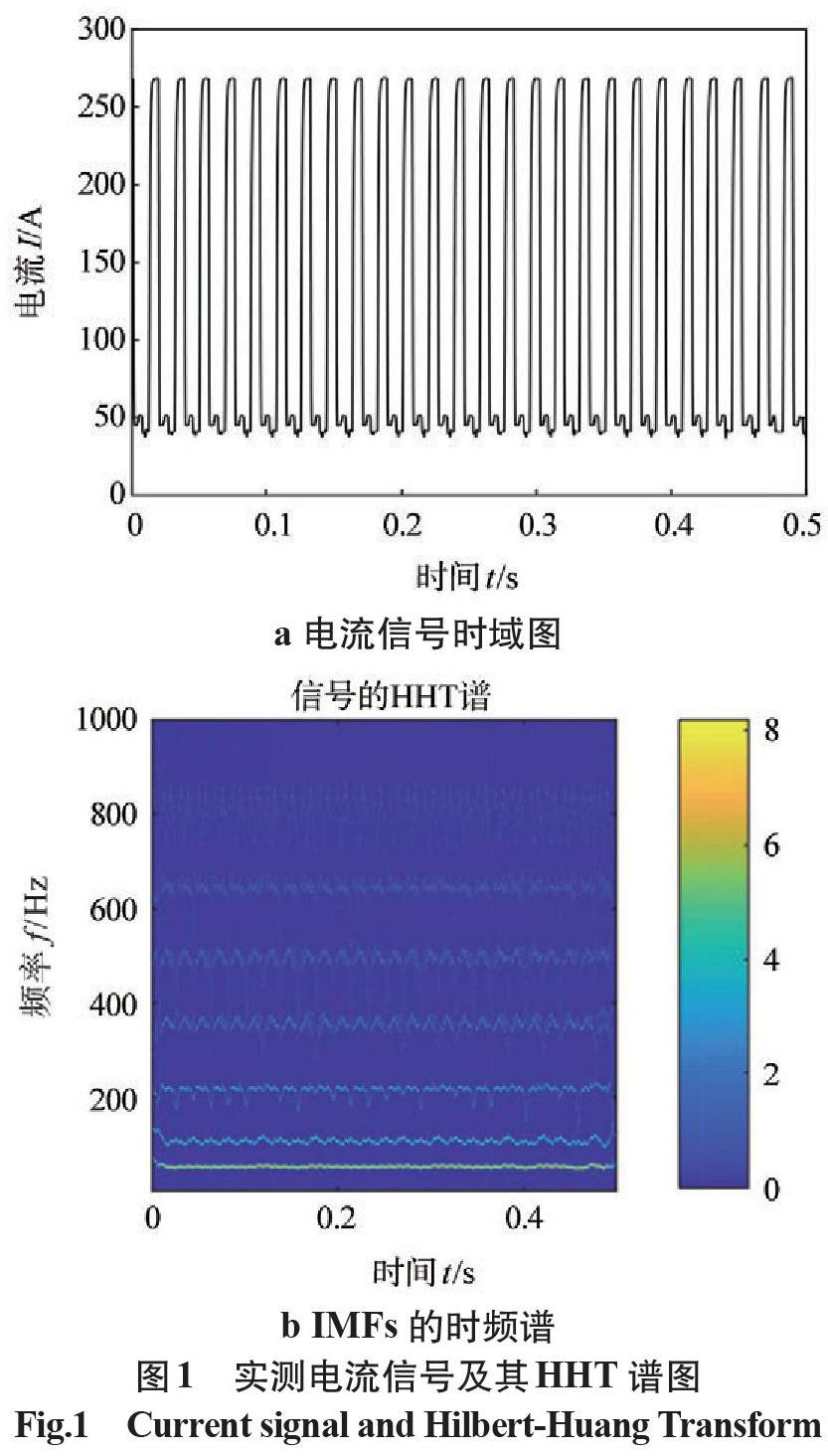
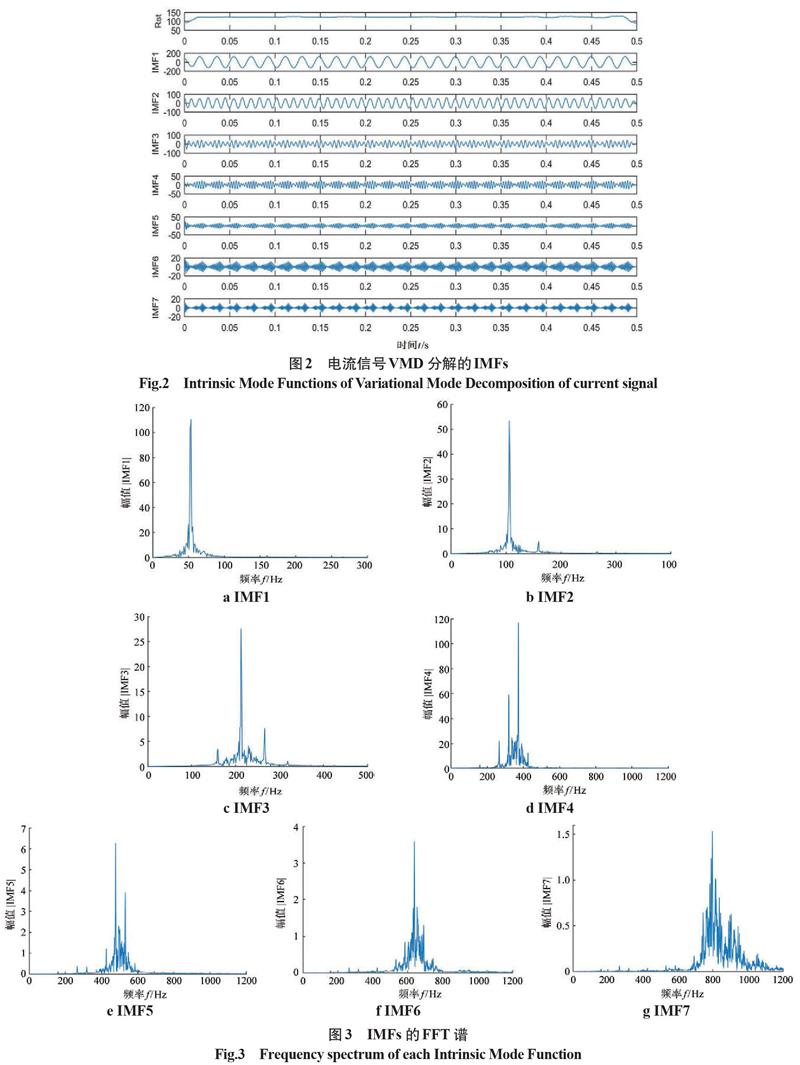
利用VMD算法对电流信号进行自适应时频分解，得到7个本征模态分量IMFs和1个残余分量（见图2），从IMF1～IMF7的局部极值点间隔可以清晰地看出原始信号的熔滴过渡周期是均匀的且频率逐渐变大，但其幅值逐渐变小。对本征模态分量进行傅里叶变换，将其转变为焊接信号频率随幅值的变化关系（见图3），从7个IMF的FFT谱图中可以看出，IMF1分量的幅值最大且远大于其他分量，说明焊接电流信号的频率能量主要集中在低频区域，约为55 Hz。

2.1.2 电弧电压信号的分解

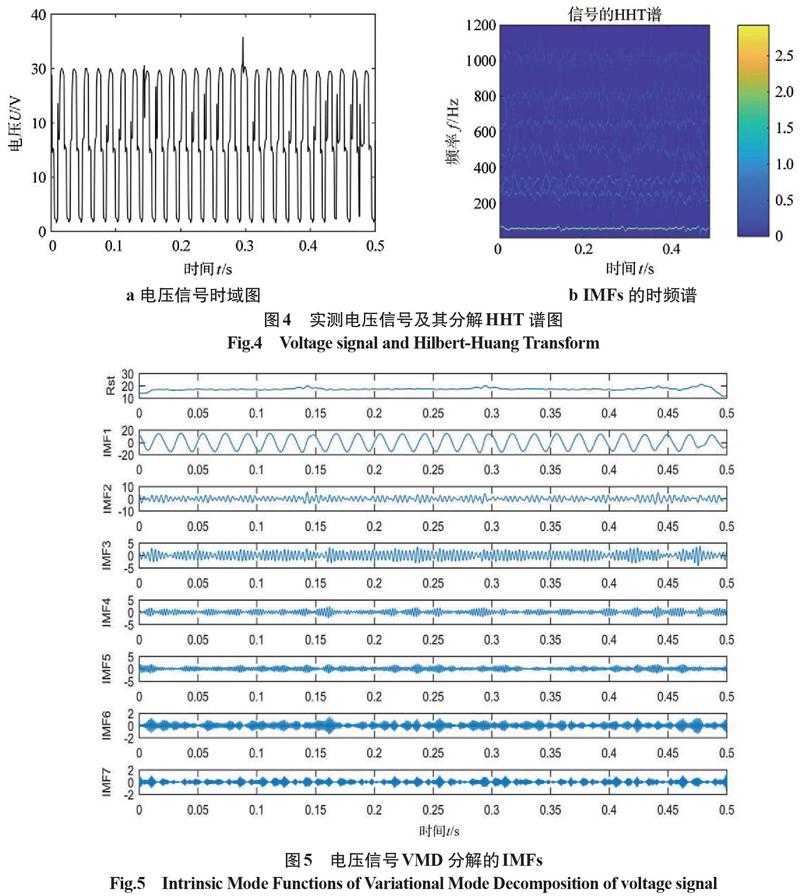
电弧电压分解具体波形如图4～图6所示。图4为实测电压信号及其分解HHT谱，图4a为电压信号的时域图，峰值电压约为30 V，峰谷电压约为2 V，峰值电压出现尖峰且电压上升阶段出现混杂。图4b为实测电压信号VMD分解分量经希尔伯特转变得到的焊接信号时频谱图，可以看出，IMFs对应的频率有7个，由于模态数k=8，说明还有一个残余分量。且分解频率越低，HHT谱中的线越平滑，频率越高，线形越混杂，总体均匀分布在一个范围内。

电压信号VMD分解分量示意图如图5所示，共有7个IMFs分量和1个残余分量。从IMF1～IMF7分量的局部极值点间隔明显看出，原始信号的熔滴过渡周期均匀，分量波形幅值逐渐减小，频率逐渐增大，混频情况逐渐加剧。再对7个IMF分量进行傅里叶变换，将其转变为焊接信号的频谱图（见图6），IMF1分量的幅值最大且远大于其他分量，说明焊接电压信号的频率能量主要集中在低频区域，约为55 Hz。

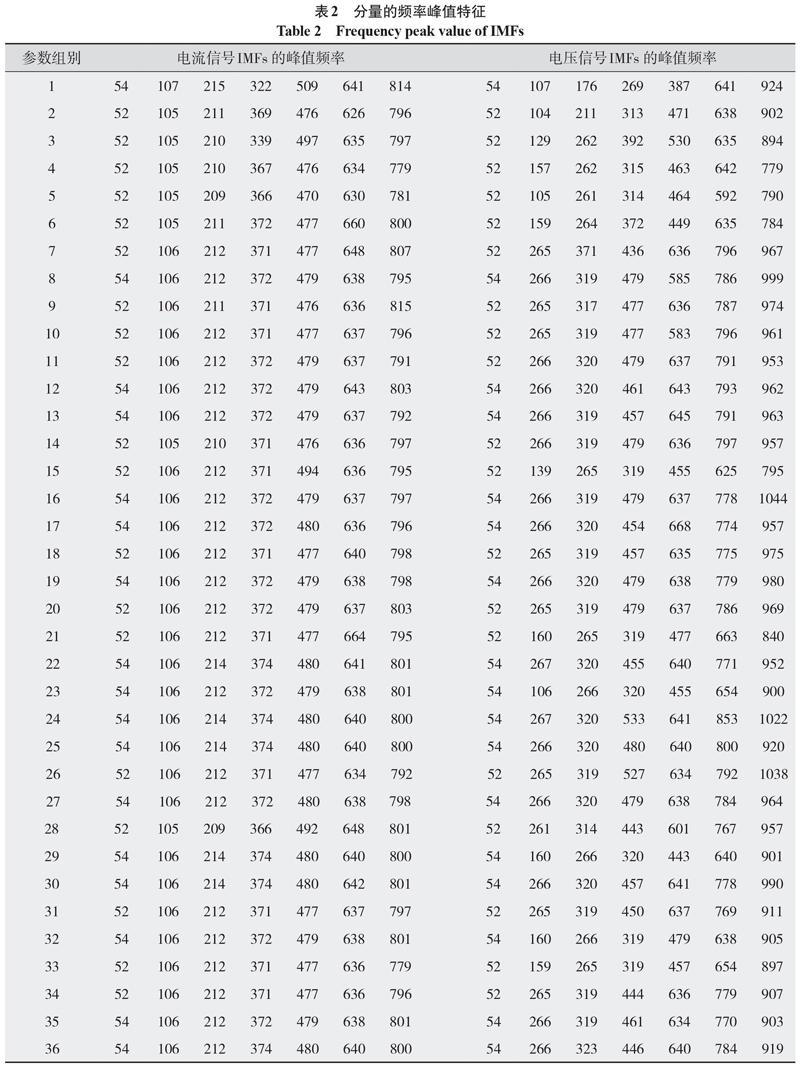
将采集到的实测电信号按上述方法原理进行分解，以电流与电压IMFs分量的FFT谱的峰值频率为特征参数。对采集的数据进行预处理，去除每道焊缝电弧引弧和熄弧阶段各1 s的数据，并将每道焊缝分为时间步长为0.5 s共5 000个数据段进行分析，得到特征参数值，为后续分析奠定基础。采用标准工艺参数所得第5层焊道36组数据段的时频特征值如表2所示。

2.2 电弧信息与熔宽关系建模

处理、分析电信号并提取其特征的目的是预测熔宽。由电信号的时频分析可知，电信号对焊缝成形特征较为敏感，但其提取出的特征值不止一个，它与成形质量的关系难以用数学公式表达，所以需要建立数学模型来识别不同焊接质量。文中建立GMA焊接質量支持向量机（SVM）模型，以提取出来的特征值为输入量对模型进行训练测试，以此预测多层多道焊接熔宽信息。根据表1中不同送丝速度获得的多层多道焊缝，选取最后一道焊道进行数据分析，提取特征参数。

2.2.1 数据的处理与参数的寻找

由上述时频特征值的分析可知，每类焊缝对应一个由电流电压分量峰值特征构成的14维时频特征值向量，共4种焊缝类别，具体工艺类型与类别标签对应关系如表3所示。

SVM模型的输入特征值为每种工艺条件下数组的前18组数据，共72组数据用于训练模型，余下72组数据用于测试模型的识别效果。另外，奇异数据（不同分量之间数值相差很大的输入矢量）的存在会影响模型的计算速度和最终识别结果，所以数据预处理时要消除这种影响。文中在训练SVM模型前，对数据进行归一化处理，以消除奇异数据的影响，线性函数归一化公式为：

式中 x*为归一化特征值;x为样本特征值;max为样本数据的最大值;min为样本数据的最小值。

在MATLAB中建立SVM模型，采用高斯径向基函数作为核函数，在程序中需要设定参数c和g，其中c为惩罚系数，c值越高说明越不能容忍误差。g为高斯径向基函数本身的一个参数，代表核函数的宽度。采用Grid Search CV的方法寻找参数，即网格搜索和交叉验证。网格搜索，即参数搜索，即在指定的参数范围内，按步长依次调整参数，利用调整的参数训练学习器，从所有的参数中找到在验证集上精度最高的参数，这是一个训练和比较的过程，其效率比穷举搜索高得多。文中SVM程序中设定惩罚参数c 和核函数参数g 的变化范围为[0，100]。

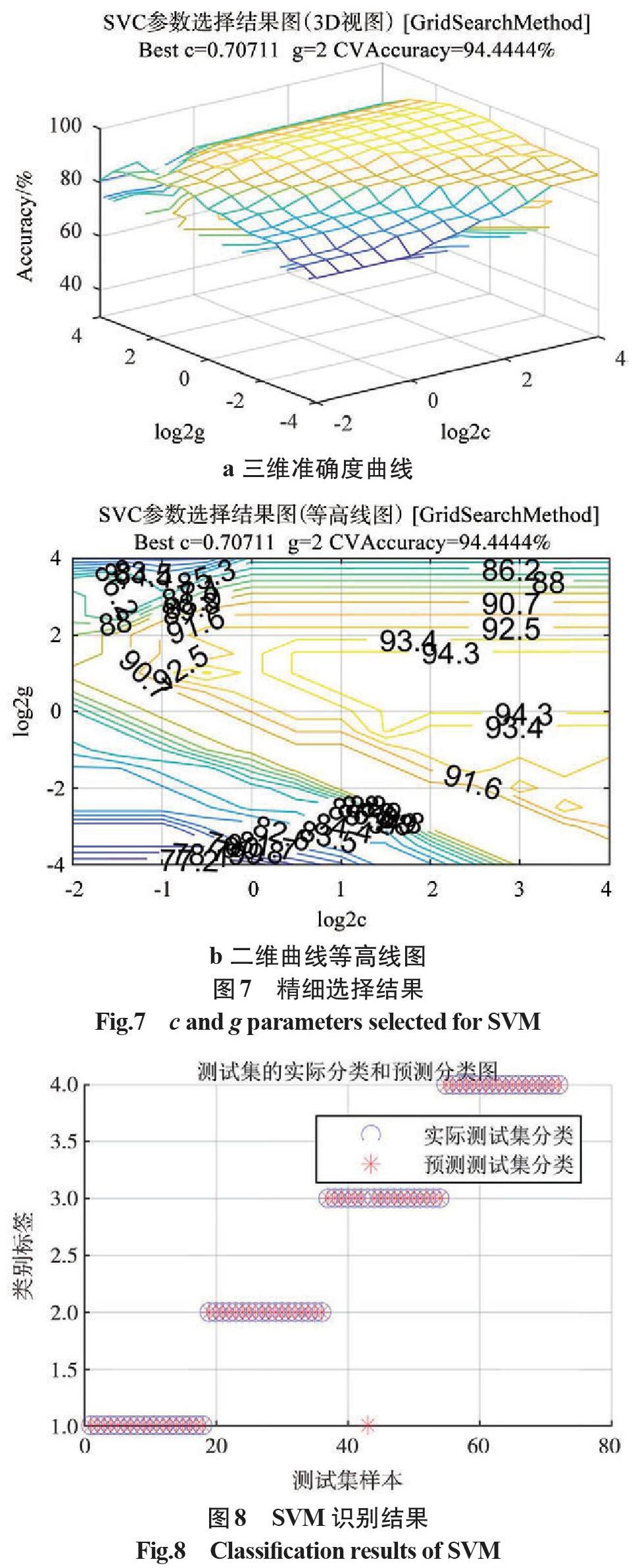
将熔宽数据输入到SVM程序中，运行后得到参数选择情况与分类预测图。CV寻参法的精细寻找如图7所示，图7a为找寻参数的3D网格图，图7b为找寻参数的等高线图，具体情况如下：精细选择c=0.707 11，g=2，准确率94.444 4%。

以VMD分解所得IMFs分量的峰值频率为特征值组，熔宽SVM模型对测试数据的识别结果如图8所示，预测准确率为98.611 1%（71/72），图中测试点只有1点游离在预测集外，证明以VMD分解的电流与电压IMFs分量的峰值频率为特征值来预测焊接质量是可行的。

3 结论

（1）利用傅里叶变换和希尔伯特变换将电信号的时域图转化为频谱图与时频图，得出其信号频率处于低频频带内，约为55 Hz，并提取了电流与电压信号IMFs分量的FFT谱峰值频率作为其时频特征参数，为后续的关系建模提供数据样本。

（2）以VMD分解的电流和电压IMFs分量的峰值频率为特征参数训练SVM模型，建立焊接熔宽与焊接质量的SVM模型，结果表明熔宽SVM模型对样本数据的识别效果较好，预测精度达到98.611 1%。

参考文献：

杨笑宇，李言，赵鹏康，等.电弧增材制造技术在材料制备中的研究现状及挑战[J].焊接，2018（8）：14-20.

张宁.自适应时频分析及其时频属性提取方法研究[D].山东：中国海洋大学，2008.

WANG Liang，HU Wei-ming，TAN Tie-niu.Recent Devel-opments in Human Motion Analysis[J].Pattern Recognition，2003，36（3）：585-601.

乔丽红，贾曼曼，梁义涛.自适应信号处理算法对比分析[J].信息技术，2018（3）：22-26，33.

黎洪松，李达.人体运动分析研究的若干新进展[J].模式识别与人工智能，2009，22（1）：70-77.

满君丰，李倩倩，温向兵.视频监控中可变人体行为的识别[J].东南大学学报（自然科学版），2011，41（3）：492-497.

周晓晓，王克鸿，杨嘉佳，等.等效电阻VMD-奇异谱熵双丝PMIG焊稳定性评价方法[J].电焊机，2018，48（4）：18-22.

罗争光.基于变分模态分解的磁控埋弧焊自动跟踪系统的研究[D].湖南：湘潭大学，2016.

范高铭.基于变分模态分解的残余应力检测及其评定方法研究[D].长春：长春工业大学，2019.