基于KMV模型的中国上市银行信用风险度量研究

（贵州大学 经济学院，贵州 贵阳 553000）

一、引言

商业银行作为金融体系最主要的组成部分，需要自身保持稳定发展，才能促进整个金融体系，甚至国家经济的长期稳定发展。但是由于商业银行具有与其他金融机构不同的特殊地位，即负责国家货币信用的运作，使商业银行的风险性成为其主要特征，如何做好风险管理也成为现代商业银行经营管理过程中最主要关注的问题。商业银行的信用风险是不良资产增长继而引发流动性危机的主要因素，信用风险本身的特殊性，加之经济活动中的很多不确定因素，信用风险越来越难以得到有效控制。风险管控，尤其是信用风险的控制，对于商业银行的持续有效运行至关重要。因此，运用现代计量模型对我国商业银行的信用风险进行测度，能够更有效地控制信用风险。KMV 模型为我国商业银行信用风险管理提出了一种新的量化分析方法，如果该模型将商业银行的实际经营情况反映得比较有效、准确，且能够预测商业银行发生违约概率的可能性，就可以在一定程度上避免和减少信用风险的发生。

二、文献综述

随着西方发达国家银行信用体系的发展，国外学者对商业银行信用风险进行了一系列的研究。Michel Crouhy 等（2000）[1]回顾了当前提出的行业担保信用风险价值评估方法，主要包括J.P 摩根银行的CreditMetrics 模型、CSFP 的CreditRisk+模型、KMV 公司的KMV 模型等。其中，KMV 模型可以通过股票市场数据直接计算信用风险，利用资本市场信息对公司违约风险进行预测，因此KMV 模型的应用相较其他模型而言更为广泛。Matthew Kurbat 和Irina Korablev（2003）[2]检验了KMV 模型作为金融机构信用风险度量工具的有效性，研究结果表明，基于KMV 模型的违约距离能够很好地反映银行的信用风险。Ke Wang 和Darrel Duffie（2010）[3]认为，KMV模型能够较好地通过计算对公司预期违约率进行预测。Kollár 等（2015）[4]通过对Merton 模型和KMV模型的比较，KMV 模型主要以股票市场的资产价值及其波动性为变量，对于市场上公开交易的公司而言运用更为方便。另外，KMV 模型的分析中涵盖多个负债种类和违约形式，与实际运用情况更为相符。

我国经济的快速发展，带动国内学者对商业银行信用风险进行了深入研究。曹道胜和何明升（2006）[5]从模型建立的理论基础、模型类别、回收率、现金流折现因子四个维度分别对CreditMetrics 模型、KMV模型、CreditPort-folioView 模型和CreditRisk+模型在中国商业银行的适用性进行分析，得出这四种模型对我国商业银行的信用风险管理都具有参考价值的结论。一些学者也对模型在我国的适应性方面进行了探讨。李磊宁和张凯（2007）[6]将KMV 模型与我国国情相结合，对沪深两市30 家ST 公司和30 家非ST 公司的信用风险进行评估检验，结果表明，利用修正后的KMV 模型，对ST 公司和非ST 公司之间信用风险的差异可以更确切的识别，对上市公司信用质量的变化趋势能够得到更准确的信息。凌江怀和刘燕媚（2013）[7]基于10 家上市商业银行2012年的数据，应用KMV 模型对银行的信用风险进行度量，并对KMV 模型在我国商业银行信用风险度量中的适用性进行检验。蒋彧和高瑜（2015）[8]利用KMV 模型对2014 年2 月我国2008 家上市公司的信用风险进行测评，验证了模型识别和信用风险预测能力。杨秀云等（2016）[9]以2013 年45 家ST 公司和与之配对的45 家非ST 公司以及2014 年20 家ST 公司和与之配对的20 家非ST 公司为样本，对样本的违约距离进行实证检验。通过实证结论提出我国商业银行在对债务公司进行信用评估时，综合运用KMV 模型和公司的财务数据，更能信任信用风险的计量结果。

本文将在前人研究的基础之上，运用KMV 模型，计算出2019 年我国10 家上市银行的股权价值波动率，再使用python3.0 对各银行的资产价值及其波动率进行计算，得出其违约点和违约距离。并通过违约距离与预期违约频率的映射关系，对我国商业银行的信用风险情况进行分析。

三、相关理论和模型介绍

（一）KMV 模型相关理论

KMV 模型是KMV 公司以现代资产定价理论的基础作依托，于1997 年推出的一种信用风险度量模型，其基础主要有Black-Scholes 期权定价公式和Merton的风险债务定价理论。该模型在信用风险的测量中运用了公司股票价值的期权特点。KMV 模型将公司的股权价值看作是一种看涨期权，股东持有的股权视为是以公司的资产价值为标的，公司负债则是股东向债权人购买的期权，期权的到期执行价格就是公司负债的账面价值。债务到期时，如果公司的资产价值低于负债价值，公司将发生违约。KMV 模型主要用于计量分析公司的违约风险，以公司的股票市场价格的变化为分析角度探究公司的信用水平情况。

（二）KMV 模型介绍

1.资产价值和资产价值波动率。根据Black-Scholes-Merton 期权定价模型，公司股权价值和资产价值的关系如下：

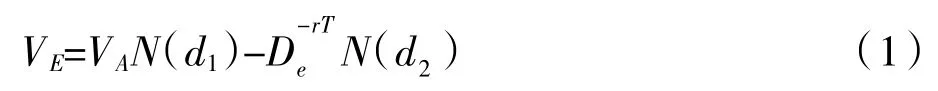
公司的股权价值波动率与资产价值波动率的关系如下：

在公式（1）和（2）中，VE为公司的股权价值，VA为公司的资产价值，D 为公司的负债，T 为公司债务剩余期限。r 为无风险利率，σE为股权价值波动率，σA为资产价值波动率，N（d）为标准正态累积分布函数。联立两个方程进行计算，就可以得到资产价值VA及资产价值波动率σA。

2.违约点DP 和违约距离DD。在KMV 模型中，债务人在期限内不能全额偿还的本金和利息即称为违约。从理论来说，在公司的市场价值低于其负债水平时会发生违约，但是长期负债会对公司的偿债能力有所缓解。KMV 公司经过多次实证研究，发现触发违约最频繁的临界点是公司价值约等于公司短期负债与0.5 倍的长期负债之和，也即是公式（3）。而违约距离是指公司资产的期望值和触发违约的临界价格点之间的相对距离。违约触发点DP以及违约距离DD 的计算公式如下：

其中，STD 为短期负债，LTD 为长期负债。

其中，E（VA）为公司资产的期望值，根据资产价值VA确定。DD 越大，违约风险越小；反之，公司的违约风险就比较大。

3.预期违约频率EDF。在资产价值服从标准正态分布的假设下，根据对违约距离DD 的理解，从理论算法得出的预期违约频率如下：

由公式（5）可得，违约距离DD 越大，公司不按时偿还债务的可能性越小，信用风险越小，反之亦然。违约距离DD 和预期违约频率EDF 呈负相关关系。

四、实证部分

（一）数据选取

本文选取我国的10 家上市商业银行作为样本，其中包括国有商业银行、股份制商业银行，时间测度为2019 年。各样本银行的股票代码如表1 所示。

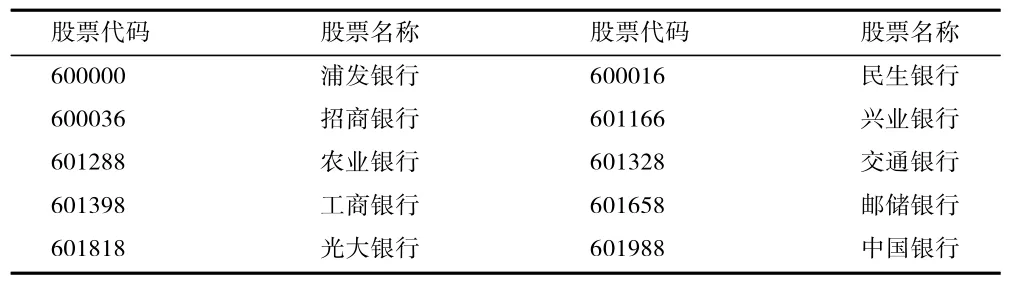
表1 各样本股票代码

（二）参数设定

本文所设定参数包括：

股权价值（VE）：股票价格与市场中流通股数量相乘。

违约点（DP）：流动负债与0.5 倍的长期负债之和。

无风险利率（r）：以中国人民银行的一年期定期存款利率作为无风险利率，即=1.5%。

时间参数（T）：设定违约距离的计算时间为一年。

股权价值波动率（σE）的设定：在模型中，假设收益率序列是平稳的且服从于正态分布，可以采用统计方法分析和预测收益率的波动率。

（三）实证过程

1.计算各样本银行的股权价值（VE）。假设股票价格=加权收盘价=（最高价+最低价+收盘价×2）/4，计算结果如表2 所示。

表2 股权价值 单位：百万元

2.计算各样本银行的股权价值波动率（σE）。通过参考相关文献股票波动率的计算方法，考虑到数据的可行性，本文假设股票价格近似服从于对数正态分布，通过对历史数据的估算得出股权价值波动率。将股票的对数收益率定义为：μi=，其中Si表示第i 天的收盘价，μi表示第i 天的收益率。股票价格的日收益波动率σ 可以通过其标准差表示，即。将股票价格带入该式，得到股票价格的日收益波动率。本文假设股票一年中的交易天数为252 天，可以将股票价格的日收益波动率换算为年收益波动率σE=σ×，其中n 为一年中的交易天数。根据以上的方法设定，算得所选的10 家商业银行的年化收益波动率即股权价值波动率，结果如表3 所示。

表3 股权价值波动率

3.计算各样本银行的资产价值（VA）及资产价值波动率（σA）。将表2、表3 中的结果带入期权公式中计算，结果如表4 所示。

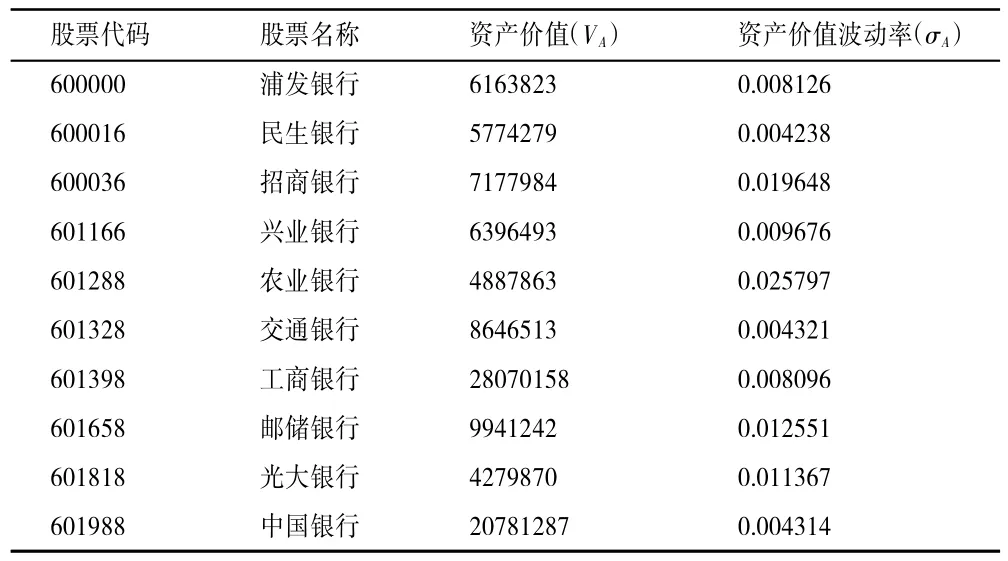
表4 资产价值及资产价值波动率 单位：百万元

4.计算各样本银行的违约距离DD 和预期违约频率EDF，并根据上述实证结果，作出各样本银行的违约距离折线图，如图1 所示。

图1 违约距离折线图

表5 预期违约概率

五、结论及建议

（一）结论

在本文的研究中对我国的10 家上市商业银行面临的信用风险进行了测度分析，利用KMV 模型定量地计算得到各银行的违约距离和预期违约频率。根据本文的实证结果可以看出，资产规模对违约距离的影响显著。商业银行资产的规模越大，即盈利水平和偿还债务的能力越强，违约距离也就越大，说明该银行的预期违约频率较小，所面临的信用风险较低；相反，如果商业银行的资产规模越小，且在运行过程中股票价格出现大幅波动，则说明其预期违约频率就越大，面临的信用风险也相对更高。违约距离可以较好地反映银行的信用质量实情，违约距离越大说明银行的信用质量越好。

总的来说，在实证过程中KMV 模型由于数据获取比较容易，计算过程简便，对我国现阶段的商业银行信用风险测度来说有较好的实用性。由于KMV 模型对违约风险具有一定的预测能力，可以将违约距离作为一个商业银行信用风险的预警指标，为及时发现风险从而规避或消除风险提供参考价值，这对于商业银行开展资产负债业务也具有重要的借鉴意义。因此，商业银行在进行自身的信用风险管理时，不仅可以利用信用等级评估结果进行参照，也可以通过运用KMV 模型的计量对信用状况进行深入分析。但是，由于我国没有完整的历史违约数据库，缺少实际违约距离和预期违约频率的映射关系，这使得KMV 模型在我国的实际运用过程中仍存在部分缺陷，即仅根据假设违约距离和预期违约频率之间服从的标准正态分布计算出的预期违约频率偏小，可能会导致我国银行的违约风险被低估，不能很好的把握信用风险管理。

（二）建议

虽然在实证分析中可以看出运用KMV 模型对我国上市银行的信用风险进行度量具有较强的实用性，但是KMV 模型在使用时仍然存在一些不足，也需要进一步对模型进行完善改进，增强该模型在我国上市银行信用风险分析中的适用性。为了加强对我国银行业的信用风险的控制，对其实施更为有效的监管策略，以及为完善我国银行业的信用风险防范预警体系，促进银行业的健康稳定发展，本文提出以下三点建议：

第一，要逐步建立起我国的上市公司信用风险违约数据库，加强对信用风险相关数据的积累和管理，通过积累的历史数据建立我国上市公司的违约距离和违约概率之间的映射关系，以数据为基础运用KMV 模型对我国上市公司进行信用风险分析。

第二，KMV 模型的基础数据是来源于上市公司的年度报表和各交易日波动的股权信息，只有确保公司财务数据的真实准确，KMV 模型才能反映上市公司真正的信用风险状况。因此，监管部门应加强市场监督，完善我国上市公司的治理结构，防止公司披露虚假的财务数据。与此同时，上市公司也要规范运行，公司必须发布真实准确的财务数据。只有这样，KMV模型才能准确发挥其动态预测信用风险的能力。

第三，商业银行应立足于内部控制，从内部入手，提高自身风险管理水平。在实际运用过程中，商业银行要对信用风险进行全面控制，通过运用信用风险度量工具和信用风险缓释技术的结合来规避或消除风险。