单层球面网壳结构静力稳定性研究
陆世宇 陈大龙 冯冲冲
(江西理工大学建筑与测绘工程学院 江西赣州 341000)
网壳结构的稳定性计算方法经过了多年的发展历程,不同的计算方法不断的被提出。支旭东[1]等采用弧长法对均布荷载作用下的带屋面系统的单层网壳结构进行非线性数值模拟,得出该条件下对结构稳定性的影响。黄卫林[2]研究了对K6型单层球面网壳结构静力稳定性的一些影响因素:节点构造、缺陷大小,并给出结构在不同参数下的变化规律。本文在已有研究的基础之上,总结了矢跨比、初始缺陷这些参数对网壳结构稳定性的影响规律。
1 结构屈曲分析
结构屈曲[3]是结构材料应力还未达到其极限强度时就失稳的现象。屈曲模态就是结构该状态下位移的变化量,研究结构的屈曲模态[4],可直观的找出结构薄弱部位及结构各节点的位移增长趋势。屈曲模态包括局部屈曲和整体屈曲[5],局部屈曲包含杆件屈曲和点状屈曲,条状屈曲则属于整体屈曲的范围。特指值屈曲就是理想网壳结构随着外荷载的不断增大,位移不断增加而出现的不同于初始平衡状态的另外一种平衡状态。结构可能的屈曲形状可以通过特征值屈曲分析的结果来进行预测,也可以计算出屈曲荷载的理论最大值。
2 凯威特网壳结构参数分析
2.1 矢跨比的影响
计算模型为跨度为60m,杆件截面设为φ140×4mm,采用一致缺陷法,初始缺陷值取L/300,周边固支,施加均匀分布荷载,分析在静力作用下不同矢跨比(f/l=1/2、f/l=1/3、f/l=1/4、f/l=1/6)对结构稳定性能的影响规律。
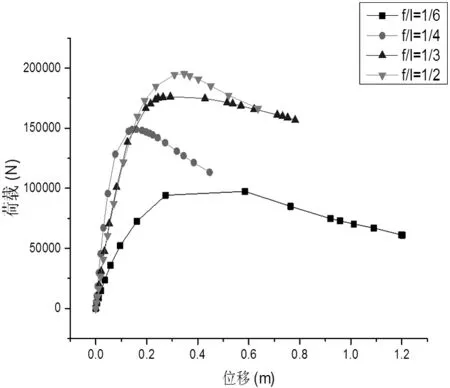
图1 不同矢跨比下的荷载-位移曲线
从图1可看出:初始加载阶段下的荷载位移基本呈线性关系迅速上升,结构的整体刚度较大,在接近临界荷载时杆件屈服较大,结构刚度明显下降。矢跨比从1/3~1/2变化中,结构刚度逐渐变大,相应的极限承载力也随之增大。由于凯威特网壳结构主要是径向传力,其失稳区域往往发生在径向主肋上,随着矢跨比慢慢减小,失稳区域慢慢向中心靠近,此时结构极限承载逐渐增加。
2.2 初始缺陷大小的影响
研究凯威特球面网壳对于初始缺陷的敏感度,本文从缺陷大小这个方面出发,对网壳结构进行稳定性分析。参数设置的方案为跨度为60m,矢跨比为1/2的K6型网壳,采用一致缺陷法施加缺陷大小分别为L/100、L/200、L/300、L/400、L/500。
按照上述方案设置的凯威特网壳均为1/2矢跨比的大跨形式,其中K6型网壳的荷载-位移曲线如图2所示。
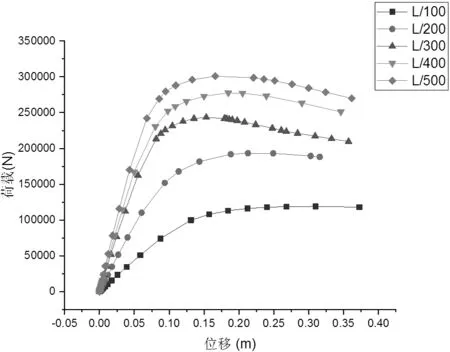
图2 几种缺陷值下的荷载-位移曲线
从图2可得出:随着初始缺陷值不断变小,结构的极限承载力则不断变大,因此网壳结构对初始缺陷十分敏感。结构承载力在初始缺陷在L/100到L/200之间时与其他缺陷值相比上升最为显著,但是到了L/300这一阶段,结构承载力上升趋势逐渐变缓,结构整体刚度变化不大,由此可得,大矢跨比凯威特网壳虽然是同类网壳结构稳定性较好的一类,但对于缺陷施加大小同样非常敏感。
3 结论
本文主要研究了凯威特单层球面网壳结构的静力稳定性,得出如下结论:
(1)在合理的范围内,不同矢跨比结构其极限承载力随着矢跨比的增加而提高,即适当加大矢跨比有利于提高网壳结构的静力稳定性和刚度。
(2)网壳结构对初始缺陷十分敏感,当初始缺陷值逐渐降低时,结构极限承载力随之增大。通过观察绘制的荷载位移曲线,建议在结构设计的时,可以在初始缺陷值L/300,L/500条件下做一个稳定性验算。

