几类常见函数的极限计算方法

孟献青

（山西大同大学数学与统计学院，山西大同 037009）

极限是高等数学的重要内容，也是高等数学的重要思想方法和研究工具，是高等数学学习的第一个难关，尤其它的思维方式和思考方法对学好高等数学非常重要。极限的求解方法灵活多变，技巧性强[1-3]。文章对几种常见函数的极限计算方法进行了归纳和总结。极限运算法则、洛必达法则、分子（分母）有理化、无穷小的性质，极限存在总则，这些都是求极限常用的方法，下面对几种常见函数的极限方法进行研究。

1 分式函数的极限

1.1 利用极限运算法则求极限

极限运算法则是计算极限最基本的依据，对于多项式函数而言，求极限可以直接计算函数在该点的函数值，但对于分式函数而言，如果分母的极限不为零，那么可以直接求函数在该点的函数值，然后应用极限运算法则求解。

1.2 利用无穷大与无穷小的关系求极限

如果分式函数分母的极限为零，分子极限不为零，可用无穷大与无穷小的关系求极限。

1.3 利用消去零因子法求极限

如果分子极限也为零，此时根据所给函数的特征，可以利用消去零因子法，也可以利用洛必达法则。如

例3求

解当x→1 时，分子，分母极限都趋于零，先约去零因子x-1，再求极限。

1.4 利用洛必达法则求极限

例3的第二种解法。

解型，利用洛必达法则得

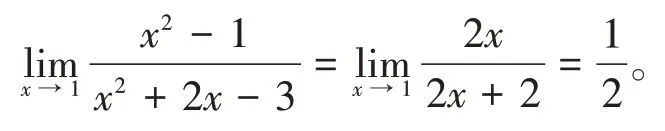
如果分子分母的极限都趋于∞，此时可以分出无穷小求极限，也可以利用洛必达法则。

1.5 利用无穷小分出法求极限

例4

无穷小分出法:分子分母同除以分母中自变量的最高次幂,分离出无穷小,然后再求极限。

解x→∞时，分子分母的极限都趋于∞，分子分母同时除以x3，分出无穷小，再求极限。

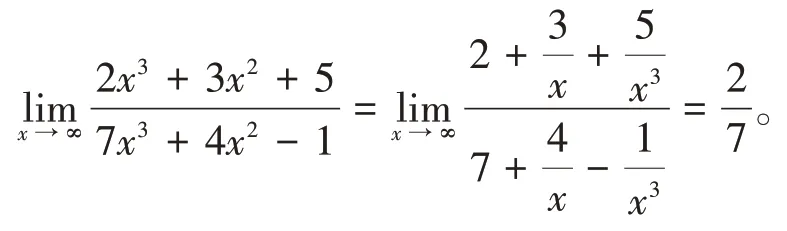
例4也可用洛必达法则求解。

对于例4而言，利用无穷小分出法求极限比洛必达法则更为简便快捷，所以对于例4 这种类型，常用无穷小分出法求解。

结论当a0≠0,b0≠0,m,n为非负整数时，有

1.6 利用无穷小的性质求极限

例5求

解当x→∞时，为无穷小，而sinx是有界函数，所以由无穷小的性质得

1.7 利用等价无穷小替换求极限

常用的等价无穷小替换，当x→∞时，sinx～x，tanx～x，arcsinx～x，arctanx～x，ln(1+x)～x，ex-1～x，

注意：利用等价无穷小替换时，必须对函数的因子或整体进行无穷小代换，当分子或分母中含有和式时，不能将和式中的某项或某几项进行代换。如上式中，不能直接将x-sinx替换成x-x，否则容易出现错误。

数列可以看成自变量为正整数n的函数，为了叙述统一，此处称为数列函数。

2 数列函数的极限

2.1 利用通分化简求极限

结论：有限个无穷小的和是无穷小，但无限个无穷小的和未必是无穷小。

2.2 利用极限存在准则求极限

极限存在准则有夹逼准则和单调有界准则，主要方法是进行放缩，然后再求极限。

2.3 利用级数收敛的必要条件求极限

由收敛级数的必要性知，如果级数收敛，则一般项趋于零。所以若以数列的通项为一般项的级数的敛散性容易判定，此时可以考虑用级数收敛的必要条件求极限。

3 幂指函数的极限

定义1底数与指数中都含有变量的函数，称为幂指函数，记为u(x)v(x)，其中u(x) ＞0,u(x) ≠1。

幂指函数求极限，常用方法如下：

（2）若limu(x)=a＞0,limv(x)=b，则limu(x)v(x)=ab；

（3）利用对数恒等式

u(x)v(x)=ev(x)lnu(x)，

则

limu(x)v(x)=limev(x)lnu(x)=elimv(x)lnu(x)。

注意：这里的lim 都表示在自变量同一变化过程中的极限。

3.1 化简成重要极限的形式求极限

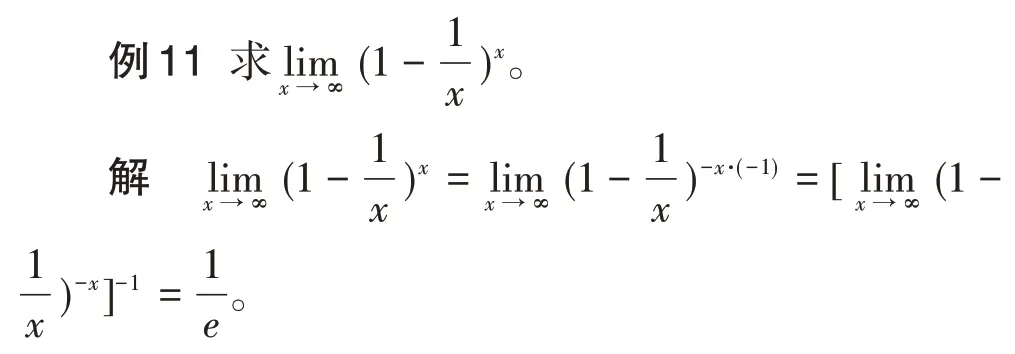
3.2 利用对数恒等式求极限

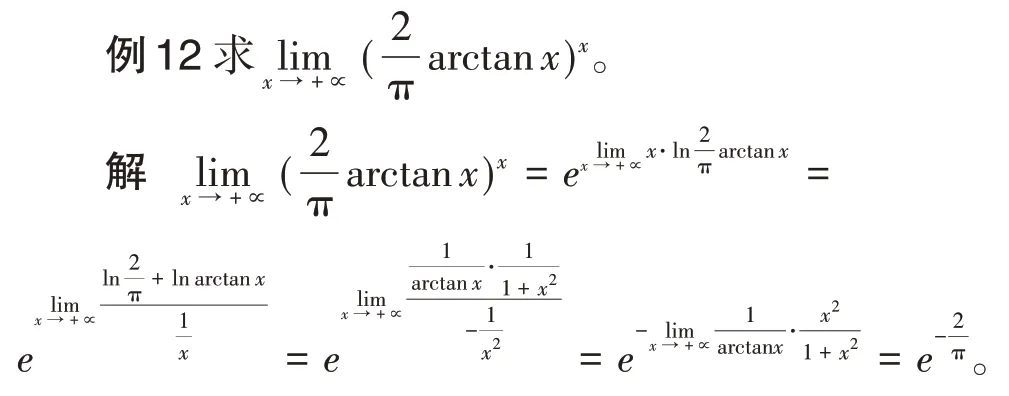
在求函数极限时，经常要把几种方法综合使用，这样才会简化计算。

4 分段函数的极限

4.1 利用左右极限求分段点处的极限

讨论分段函数f(x)在分段点x0处的极限，一般应根据左右极限来判断，如果f(x)在点x0处左右极限存在且相等，则极限存在，否则极限不存在。

例13设

解x=0是函数的分段点，左右极限分别是

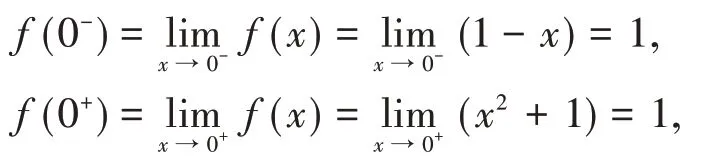
4.2 利用夹逼准则求分段函数的极限

定义2不超过x(x∈R)的最大整数称为取整函数，记为[x]。

如果函数表达式中包含取整函数，则通常用夹逼准则求极限。

对分式函数，数列函数，幂指函数及分段函数的极限进行了分类探讨，进而对极限的概念和思维有了更深刻的认识，极限的计算方法灵活多样，想要巧妙求解极限，除了多做练习，还要对求解方法进行归纳分析，这样才能不断提高应用能力。