基于蛙跳退火粒子群算法的民航发动机单元体修理级别决策及成本优化
张 青,郑 岩
(中国民航大学航空工程学院,天津 300300)
(∗通信作者电子邮箱zhangqing.guagua@163.com)
0 引言
民航发动机维修是航空公司所面临的一个重要课题,航空公司通过维修保持发动机适航性,提高发动机运行可靠性,从而降低发动机维修费用,是降低飞机运营成本的关键。发动机维修包括在翼维护和下发翻修,在翼维修主要通过定期维护和日常故障排除来保持发动机的持续适航和安全工作,航线维护成本相对固定,而不同的下发送修方案会对发动机翻修成本影响较大。大修方案决定了发动机进厂后的修理范围和内容,不同的修理内容不但会影响单元体的分解程度,而且也会直接影响修后发动机的性能恢复程度、可靠性恢复程度和翻修后的在翼飞行时间[1-2]。通常发动机生产厂家会提供一套发动机修理工作包制定指南,这套指南指导手册会详细给出每一个单元体不同级别的维修内容。一般维修期间要更换及维修的零部件及附件数量有上万个,占60%~70%的车间修理费用是更换零部件及耗材产生的。发动机的性能恢复和限寿件的更换综合起来占发动机大修费用的70%~80%。大多数的发动机修理工作范围需要考虑发动机限寿件的剩余寿命情况[3-5]。
航空发动机送修方案问题的研究引起了越来越多国内外学者的关注。赵洪利等[6]以遗传算法为基础,研究了民航发动机送修工作范围决策问题。付旭云等[7]以启发式搜索算法为基础,建立多寿命件机会更换问题优化模型并求解。赵洪利等[8]基于聚类分析中的K-means 算法来预测发动机拆发时间。马小骏等[9]基于最小二乘支持向量机算法和性能可靠性来预测航空发动机的在翼寿命。郑波[10]利用改进的粒子群优化算法对支持向量机参数进行寻优,研究民航发动机送修等级决策方法。白芳等[11]基于排序规则优化对发动机群维修成本控制方法进行了研究。付旭云等[12]基于寿命件研究了民航发动机送修目标的确定方法。国外学者研究基于遍历的发动机翻修工作包的优化方法[13],提出基于层次分析法(Analytic Hierarchy Process,AHP)和遗传算法(Genetic Algorithm,GA)混合算法去解决飞机发动机维修调度问题,数学模型是一个多目标、多约束的优化问题[14]。发动机制造生产厂家P&W(Pratt & Whitney)和R&R(Rolls-Royce)等通常会提供一套发动机修理工作包制定指南,包括WPG(Work-scope Planning Guide)和EMP(Engine Management Program)这些指南,会列出每个单元体的维修等级和不同级别的维修内容。
综合上述研究来看,单元体不同级别的维修成本和更换限寿件材料成本及剩余寿命折合成本的研究较少。因此,本文研究依据维修指导手册中的各单元体送修逻辑图,考虑限寿件到寿更换的情况,构建发动机送修成本函数,借助智能算法在保证可靠性和安全性前提下优化送修成本,确定各单元体修理级别并进行可靠性分析。考虑到送修成本模型较为复杂,本文采用蛙跳退火粒子群优化算法是在退火粒子群优化算法中引入混合蛙跳优化算法(Shuffled Frog Leaping optimization Algorithm,SFLA)的分组概念[15],以保证解的搜索范围不会随迭代次数的增长而收缩,同时由粒子群优化算法进行分组内部的局部搜索,在粒子群优化算法中添加退火优化算法,使其在落进局部最优解时,可立刻跳跃出来,融合粒子群、退火、蛙跳三个优化算法的优点,以更快的速度和更高的精度逼近全局最优解[16],并与其他三种优化算法进行求解对比。因此,本文研究民航发动机单元体送修工作范围决策及全寿命维修成本优化问题,依据维修指导手册中的各单元体送修逻辑图及限寿件更换情况,基于蛙跳退火粒子群优化算法建立以返厂时间间隔为变量的发动机单元体修理级别决策及成本优化模型,并进行可靠性分析。
1 发动机送修成本模型构建
航空公司维修工程师科学地制定发动机送修工作范围是关键问题,如果拆发早于平均返厂时间间隔,无法充分发挥零部件的性能或者可用寿命,返厂次数会增多,即总送修成本增加;如果晚于平均返厂时间间隔,会降低发动机持续运行的可靠性,发动机部件损伤或性能衰退就会越严重,维修等级会更高,热端部件表现更为明显,导致运行事故风险成本增加。
1.1 限寿件的成本模型
在发动机本体的单元体中,一些重要的转动部件失效时会导致整个发动机破坏。限寿件一般包括转动盘、转动封严、转动轴。限寿件是美国联邦航空管理局/欧洲航空安全局规定,及局方适航指令强制性要求在厂家规定使用寿命内完成更换的发动机部件。整套限寿件的费用在发动机总费用中所占比例较大,通常在20%以上。基于安全裕度考虑,在实际发动机大修时,更换寿命件时都会有一定的剩余,通常限寿件还有5%~15%的剩余寿命时就会被更换。限寿件的更换时机将会影响发动机的平均返厂时间间隔及返厂率,而发动机翻修成本受到返厂率和平均返厂送修成本的影响,因此何时更换限寿件对控制发动机翻修成本较为关键。若更换时间过早则造成限寿件剩余寿命的浪费成本,若单独因限寿件到寿而送厂修理,维修等级为深度修理,费用为400 万~500 万美元,此维修费用远远高于寿命件提前报废而浪费的成本,因此需要在恰当送修时间及维修等级下对限寿件进行更换。
基于限寿件的成本模型,设置如下参数:Cllp,efh为限寿件单位飞行小时的分摊成本,Tllp,max为限寿件的寿命(飞行小时数),Tllp,used为限寿件累积工作的飞行小时数;n为在发动机整个寿命周期中需购买限寿件的个数,P为限寿件的材料价格,kstub为限寿件寿命的预警因子,即当限寿件的剩余寿命为(1-kstub)×Tllp,max时需要送修理厂进行更换[17]。Lyear为发动机的寿命,u为每年发动机的飞行小时数,kspare为发动机机队的备发率,kctf为飞行小时飞行循环比,依据发动机厂家手册CYCllp,max为发动机限寿件的寿命循环。

1.2 发动机单元体的成本模型
现代民用发动机依照维修单元体(module)划分,不同型号的发动机因各自机型特点送修工作范围存在差别,通常发动机制造厂商会提供一套发动机修理工作包制定指南,这套维修指导手册会详细给出每一个单元体的软时限和不同级别的维修内容。在工程实际中常依据单元体的飞行时间和状况与相应的软时限做对比,制定单元体送修等级规则,确定发动机单元体的修理级别[17]。但单元体的软时限与限寿件的硬时限是不同的,软时限不是一种使用限制且非强制性,当发动机使用时间超过软时限,只要没有故障且发动机的性能允许可以继续使用下去。在维修计划指导中建议单元体自上次大修累积工作时间达到软时限附近时进行返厂修理,由于软时限是个固定时间,为了保障修后发动机的性能,又尽量延长发动机的在翼时间,所以,在判断逻辑中,当对比单元体的累积工作时间和软时限时,不是取固定值,而是在一定的范围内取值,因此,基于维修计划指导手册定义kgroup,softtime,lower、kgroup,softtime,upper、kgroup,mli分别为软时限的下限因子、上限因子和检查因子,各单元体的维修等级一般是不同的,主要旋转部件单元体维修等级如低压压气机常分为4个等级,分别是:
1)单元体级检查(Module Level Inspection,MLI),不进行单元体级的分解,只需把此单元体从发动机拆卸下或安装上,主要是为保障单元体继续在翼使用而开展的一些检查工作。
2)检查修理改装(Check&Repair/Modification,CRM)单元体或组件需要部分分解,对某些部件或损伤部件进行检查修理或改装[18]。
3)气路性能修复(Gas Path Restoration,GPR),单元体或组件需要部分分解,对单元体进行性能恢复的维修工作,改善其可靠性和稳定性。在GPR 维修等级下,单元体自上次深度修理的累积在翼时间不归零。
4)深度维修(Heavy Maintenance,HM),即对单元体大修,单元体要完全分解进行修理、性能和稳定性的恢复。在HM维修等级下,单元体自上次深度修理的累积在翼时间归零,且可更换限寿件[6]。
但不同的单元体其维修等级是不同的,某些单元体有2个维修等级,某些单元体有3个维修等级。
影响各单元体维修等级的因素主要有:
1)单元体本次返厂自上次深度修理或新件的累积在翼时间kgroup,used;
2)若此单元体含限寿件,限寿件的寿命为Tllp,max;
3)单元体的软时限Tgroup,softtime;
4)上一次返厂单元体执行的维修等级。
因各单元体的维修等级判断逻辑不相同,所以将其分为4 类。定义维修等级ri,j:当ri,j=1 时代表MLI,ri,j=2 时代表CRM,ri,j=3 时代表GPR,ri,j=4 时代表HM,ri,j=0 代表不进行修理。
1)含限寿件的重要转动部件单元体。
维修计划手册中单元体的维修等级为HM、GPR、CRM、MLI这4个维修等级,送修时需考虑限寿件寿命和单元体的软时限。
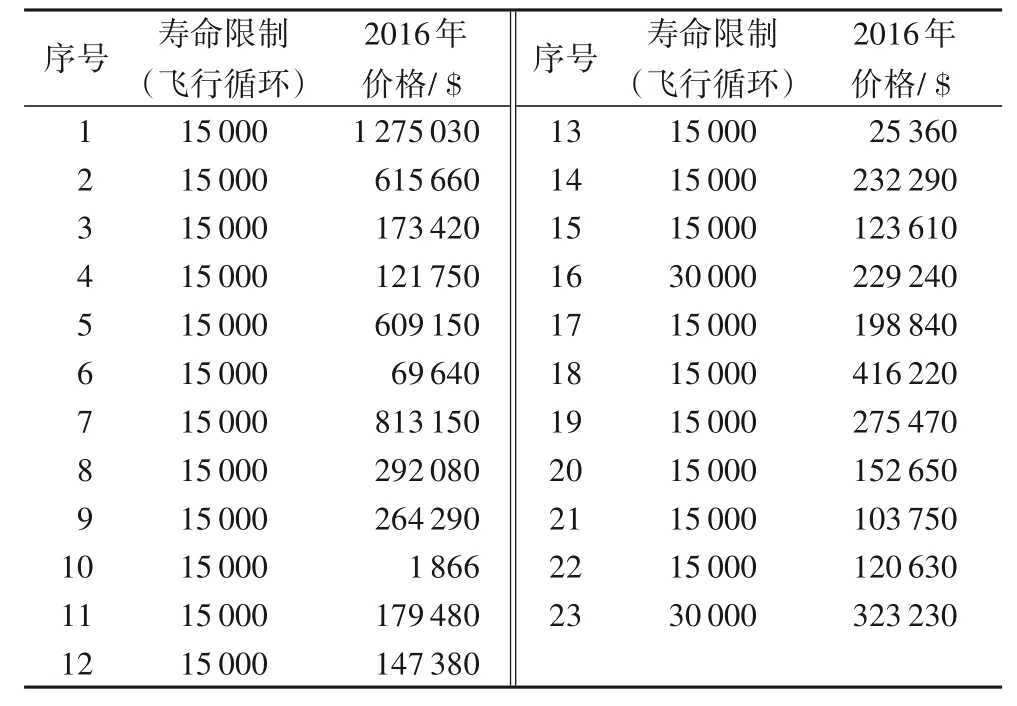
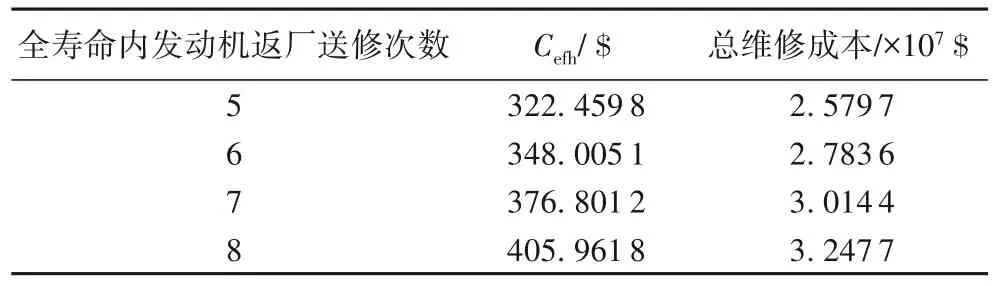
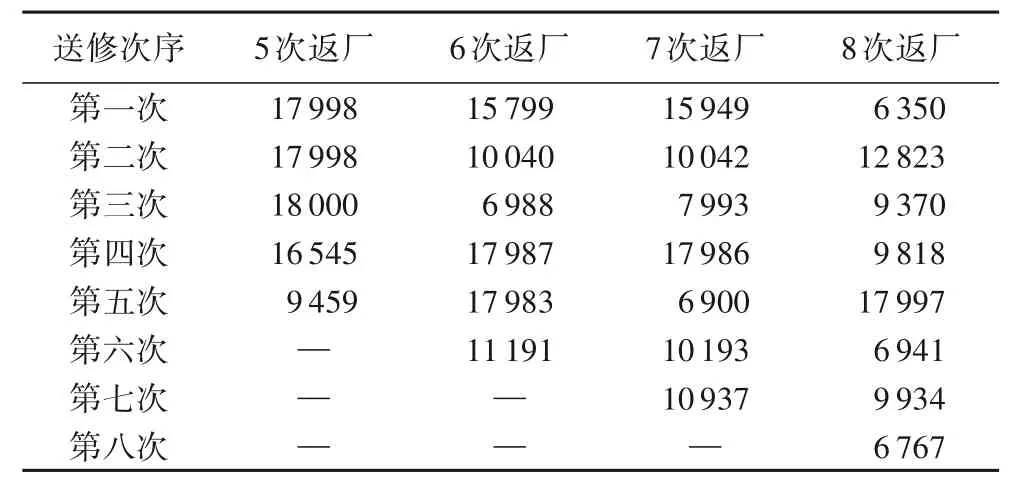
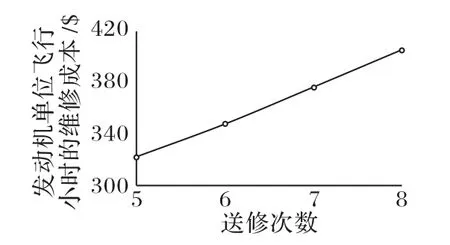
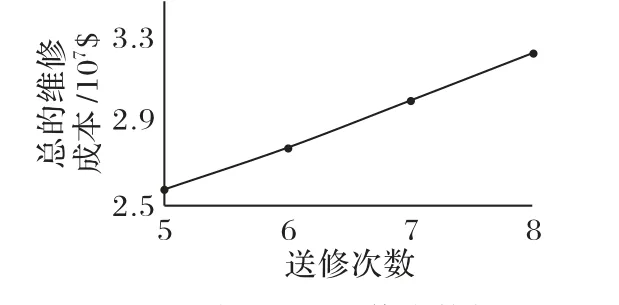
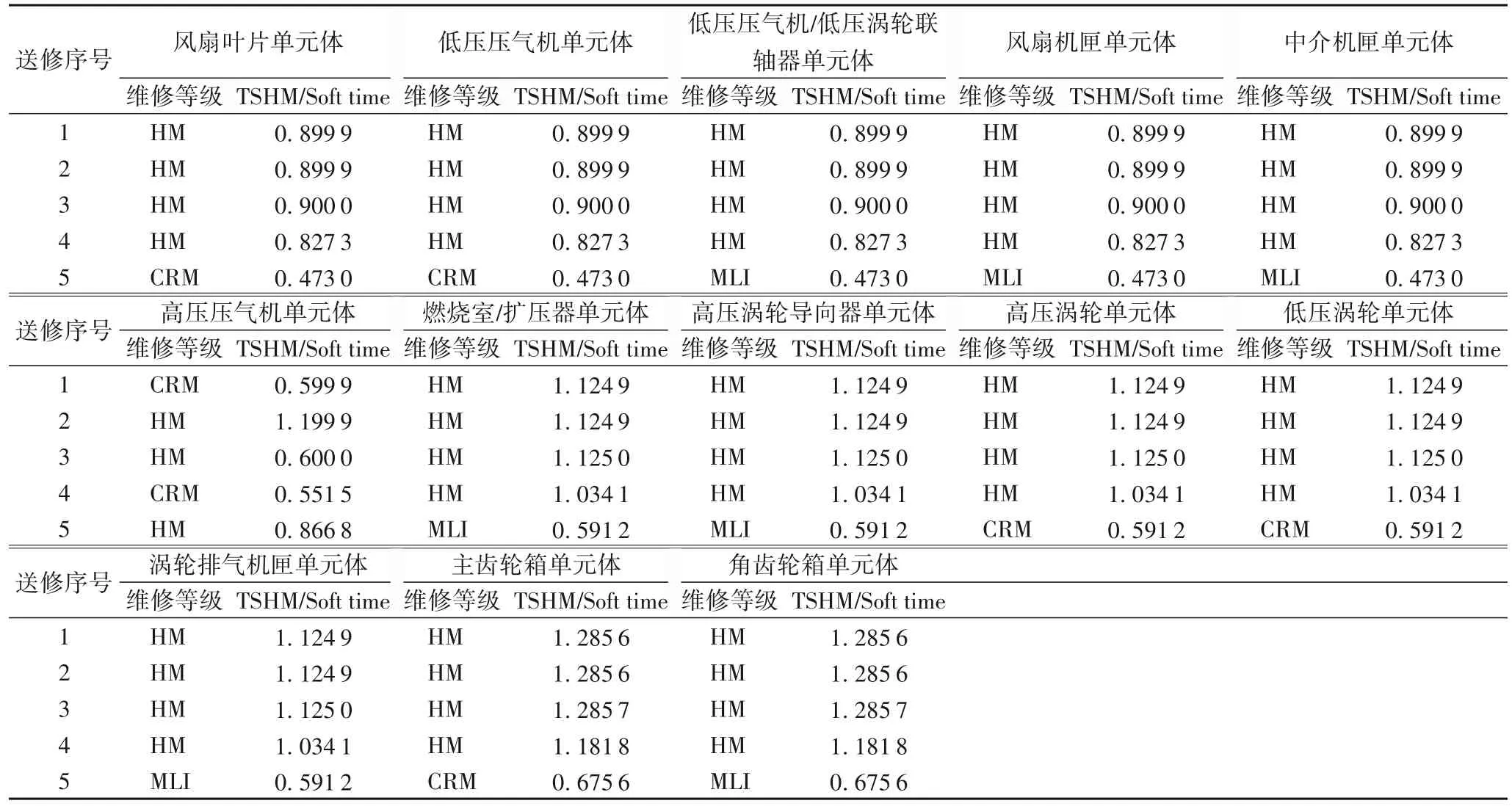
①当Tllp,stub ②限寿件累积在翼时间与下次返厂目标在翼时间Tnext,svtime加和大于限寿件寿命时,此次返厂维修等级为HM。 ③单元体自上次深度修理或新件的累积在翼时间大于单元体的软时限时,维修等级为HM。 ④单元体自上次深度修理或新件的累积在翼时间与下次返厂目标在翼时间加和大于单元体软时限上限值时,其中Tgroup,softtime,upper=kgroup,softtime,upper×Tgroup,softtime,维修等级为HM。 ⑤单元体自上次深度修理或新件的累积在翼时间大于单元体的软时限下限但小于软时限时,并判断若上次返厂送修维修等级为HM 时,则此次返厂维修等级为GPR,其他情况此次返厂维修等级为HM。 ⑥单元体自上次深度修理或新件的累积在翼时间大于单元体级检查时限但小于软时限下限时,其中Tgroup,softtime,lower=kgroup,softtime,lower×Tgroup,softtime,Tgroup,mlitime=kgroup,mlitime×Tgroup,softtime,维修等级为CRM。 ⑦单元体自上次深度修理或新件的累积在翼时间小于单元体级检查时限时,维修等级为MLI。 2)航线可更换件单元体。 维修计划手册中单元体的维修等级为HM和CRM两个维修等级,送修时只需考虑单元体的软时限。 ①单元体自上次深度修理或新件的累积在翼时间大于单元体的软时限下限,当Tgroup,usd>Tgroup,softtime,lower时,维修等级为HM。 ②单元体自上次深度修理或新件的累积在翼时间与下次返厂目标在翼时间加和大于单元体软时限上限值,当Tgroup,usd+Tnext,svtime>Tgroup,softtime,upper时,维修等级为HM。 ③单元体自上次深度修理或新件的累积在翼时间小于单元体的检查修理改装时限,当Tgroup,usd ④其他情况,单元体维修等级为CRM。 3)齿轮传动单元体。 维修计划手册中单元体的维修等级为HM、CRM、MLI 三个维修等级,送修时只需考虑单元体的软时限。 ①单元体自上次深度修理或新件的累积在翼时间大于单元体的软时限下限,当Tgroup,used>Tgroup,softtime,lower时,维修等级为HM。 ②单元体自上次深度修理或新件的累积在翼时间与下次返厂目标在翼时间加和大于单元体软时限上限值,当Tgroup,used+Tnext,svtime>Tgroup,softtime,upper时,维修等级为HM。 ③单元体自上次深度修理或新件的累积在翼时间大于单元体级检查时限但小于软时限下限,当Tgroup,mlitime ④单元体自上次深度修理或新件的累积在翼时间小于单元体级检查时限,当Tgroup,used 4)其他单元体。 维修计划手册中单元体的维修等级为HM 和MLI 两个维修等级。 ①单元体自上次深度修理或新件的累积在翼时间大于单元体的软时限,当Tgroup,used>Tgroup,softtime,lower时,维修等级为HM。 ②单元体自上次深度修理或新件的累积在翼时间与下次返厂目标在翼时间加和大于单元体软时限上限值,当Tgroup,used+Tnext,svtime>Tgroup,softtime,upper时,维修等级为HM。 ③对某些单元体需要考虑其他影响因素: a)包含限寿件的单元体:需要考虑限寿件的寿命。当Tllp,stub b)热端部件单元体:某些热端部件单元体的维修级别需考虑高压涡轮的维修等级。当高压涡轮单元体此次返厂送修等级为GPR 或HM 时,则某些热端部件单元体的维修等级为HM。 ④其他情况,单元体维修等级为MLI。 定义发动机维修总成本为Csum,维修总成本包含更换限寿件材料成本、限寿件剩余寿命折合成本、进厂固定成本和根据各单元体维修等级确定的维修成本。 式中:发动机的维修单元体数量为b;限寿件的数量为n;Cfix为进厂固定成本;发动机整个寿命周期里发生的送修次数记为D;历次返厂维修的时间间隔记为Ti;Ci,j为第j个单元体第i次送修的根据维修等级确定的维修成本;Pllp,m为第m个限寿件的价格;hi,m为第i次送修时LLP(Life-Limited Part)m是否更换,不更换时hi,m取值为0,当限寿件被更换后,Tllp,used归零,重新累积在翼时间,更换限寿件则hi,m取值为1。 定义单位飞行小时的维修成本Cefh(cost per engine flight hour): 全寿命周期内发动机单元体维修等级决策判断逻辑及送修成本模型较为复杂,因此采用蛙跳退火粒子群优化算法求解该问题。传统粒子群优化算法中每个粒子都将在d维解空间中以一定速度飞行,每个粒子的适应度代表粒子在解空间中的搜索能力,每个粒子的飞行速度由种群最优位置、粒子自身最优位置以及随机速度共同决定,通过不断迭代在解空间中寻找新解,最终使种群最优解不断接近实际最优解。由于迭代过程中粒子容易向局部最优解处聚集,本文引入退火优化算法为算法增加随机性和突跳能力,同时为增加算法全局搜索能力,引入了混合蛙跳优化算法中的分组思想。 假设某发动机返厂次数为D,定义向量x(D)为每次返厂时间间隔的向量,定义v(D)为速度向量。 将发动机分为b个单元体,每次返厂时每个单元体对应一个维修等级,定义R(D,b)为包含每次返厂时每个单元体的维修等级的矩阵。 某发动机年利用率u为1 000 个飞行循环,每飞行循环飞4 个飞行小时,kctf小时循环比为4,即每年在翼时间为4 000 飞行小时,设定发动机的寿命区间为18~20年,将其转换为飞行小时,则寿命区间为72 000~80 000 飞行小时。根据该发动机机队近10 年的拆发送修数据统计,每次返厂送修时间间隔上限为18 000飞行小时,每次返厂送修时间间隔下限为6 000飞行小时[19]。 在初始化粒子时,每次返厂时间间隔为x(i) ∈(6 000,18 000),且时间总和。由于限定条件较多,在粒子随机生成中会耗费大量时间,因此采用在中值附近随机取值的方式进行粒子初始化。 步骤2 对随机生成的粒子进行验证,即每次返厂时间间隔x(i)∈(6 000,18 000),时间总和,若不符合要求则返回步骤1重新生成粒子。 步骤3 生成速度矢量v(i)=randi(B×2)。使用成本函数计算粒子的成本值Cefh。 步骤4 重复步骤1到步骤3,生成粒子数量为N的种群,记录每个粒子当前所在位置为该粒子最好位置y,并对每个粒子的成本值Cefh进行排序,取具有最小成本值Cefh的粒子作为全局最优点Pg[20]。 根据粒子群优化算法定义,假设某粒子在t时刻所在位置为x(t),该粒子具有速度v(t+1),其表达式为: 式中:φ为压缩系数;P(t)为到t时刻为止该粒子所走过路径中最好位置;Pg(t)为粒子群整体在t时刻时最好粒子所在位置;c1、c2为学习系数;r1、r2为随机数[21]。 则在t+1时刻,粒子所在位置为: 为提高算法能力,防止其陷入局部极小值,引入退火优化算法增加算法的随机性[22]。与基本粒子群优化算法相比,该算法从诸多Pi中选择一个位置记作代替速度公式中的Pg。根据退火优化算法原理,认为Pi是比Pg性能差的特殊解,使用Pi与Pg之差去计算温度t时的突跳概率,即e-(fpi-fpg)/t,而性能越好的粒子被选中的概率越高[23]。采用轮盘赌策略从所有Pi中确定全局最优的某个替代值,从而实现退火优化算法中的随机跳动[24]。退火粒子群优化算法的速度更新公式如下: 为提高算法的全局搜索能力,本文引入了混合蛙跳优化算法中的分组思想。对于分组后的粒子群,每个分组内都有一个组内最佳位置[25],因此速度更新公式改写为: 式中:Ps代表组内最优位置;c3为组内学习因子。 本文提出的蛙跳退火粒子群优化算法是将混合蛙跳优化算法中的分组思想引入了退火粒子群优化算法之中,以保证解的搜索范围不会随迭代次数的增长而收缩[15];同时由粒子群优化算法进行分组内部的局部搜索,保证了算法的收敛速度,并且在粒子群优化算法中增添退火优化算法,使其在落进局部最优解时,可以立刻跳跃出来;最后融合粒子群、退火、蛙跳三个优化算法的优点,以更快的速度和更高的精度逼近全局最优解。蛙跳退火粒子群优化算法设计流程如图1所示。 图1 蛙跳退火粒子群优化算法设计流程Fig.1 Design flowchart of annealing frog leaping particle swarm optimization algorithm 步骤1 初始化退火温度Tk(k=0)。 步骤2 根据每个粒子的成本值Cefh对排序好的粒子进行分组,分组使用轮盘法,将整个种群分为n组,每组有N/n个粒子。 步骤3 在每个组内对粒子依照成本值进行排序,并将具有最小适应度Cefh的粒子作为组内最优位置Ps,将种群内具有最小适应度的粒子作为全局最优位置Pg。 步骤4 依据退火优化算法原理,在各个组中使用轮盘赌策略从组内粒子中选出粒子代替Ps。 步骤5 依据式(13)、(15)对粒子的位置和速度进行更新。 步骤6 计算更新后每个粒子的适应度Cefh,并判断新粒子是否符合要求范围,若粒子落在要求范围外则大幅增加该粒子的适应度Cefh。 步骤7 对粒子按照成本值Cefh进行排序,并对组内最优点Ps和全局最优点Pg进行更新。 步骤8 退火操作Tk+1=λTk。 步骤9 若未达到组内循环次数则返回执行步骤4;否则前往步骤10。 步骤10 若未达到分组次数则返回执行步骤2;否则结束循环。 下面以某台单元体结构的民用航空发动机为例,根据发动机生产厂家提供的发动机修理工作包制定指南及航空公司的数据,利用Matlab 2019 编程实现蛙跳退火粒子群优化算法。表1 为此台发动机限寿件清单,包括限寿件价格和寿命。表2 列出发动机各单元体的软时限及其上下限因子和单元体所对应的维修等级及维修成本,各单元体的软时限及其上下限因子为维修计划指南推荐给航空公司的经验值,航空公司也可根据实际运营情况进行调整。 表1 发动机的限寿件清单Tab.1 List of life-limited parts for engine 假设发动机各单元体每次进厂送修不同级别的维修成本是固定不变的,且维修成本中不包含限寿件的材料成本,限寿件成本需根据式(1)~(4)单独计算。其中,kstub限寿件寿命的预警因子为0.85,发动机机队的备发率kspare为25%,发动机寿命Lyear为20 年,kctf小时循环比为4,航线可更换的风扇单元体kgroup,mli为0.24,而其他单元体需拆发送翻修厂进行检查,单元体级检查因子kgroup,mlt为0.35。低压压气机单元体包含1 号和2 号限寿件,高压压气机单元体包含3 号至7 号限寿件,高压涡轮单元体包含8 号至13 号限寿件,低压涡轮单元体包含14号至22 号限寿件,联轴器包含23 号限寿件。低压压气机(Low Pressure Compressor,LPC)、高压压气机(High Pressure Compressor,HPC)、高压涡轮(High Pressure Turbine,HPT)和低压涡轮(Low Pressure Turbine,LPT)属于第一类含限寿件的重要转动部件单元体,共四个维修等级。风扇属于第二类航线可更换件,共两个维修等级。主齿轮箱(Main GearBox,MGB)属于第三类齿轮传动单元体,共三个维修等级。风扇机匣、中介机匣、涡轮排气机匣和角齿轮箱属于第四类其他单元体,共两个维修等级。联轴器属于第四类中包含限寿件的情况。燃烧室/扩压器高压涡轮导向器属于第四类中热端部件的情况。 为验证蛙跳退火粒子群优化算法对于该问题的适用性以及准确性,采用蛙跳退火粒子群优化算法与传统粒子群优化算法、退火粒子群优化算法、混合蛙跳优化算法进行对比,算法参数设置为:种群总粒子数N=1 000,总迭代次数为M=500,以全寿命周期内发动机返厂修理次数共5 次为例,粒子群类算法中学习因子c1=c2=2,c3=0.8,蛙跳类算法中分组数n=10,分组后迭代次数m=50,仿真结果如图2所示。 表2 发动机各单元体的软时限及单元体所对应的维修等级和维修成本Tab.2 Soft time limit,corresponding maintenance level and maintenance cost of each engine module 图2 不同优化算法的仿真结果比较Fig.2 Comparison of simulation results among different optimization algorithms 从仿真结果可以看出,蛙跳退火粒子群优化算法能够有效地避免陷入局部最优的情况发生,在四种优化算法中得到了最优的结果;对于退火粒子群优化算法和混合蛙跳优化算法来说,虽然两种算法都提高了随机性,增强了全局搜索能力,但在面对复杂问题时依然会较早地陷入局部最优的境况中,虽然有跳出局部最优的可能,但会立刻落入其他的局部最优解。由于智能算法求解具有随机性,因此每种优化算法各进行50 次仿真,并对优化算法仿真结果进行统计,四种优化算法仿真结果如表3 所示。蛙跳退火粒子群优化算法仿真结果如图3(a)所示。退火粒子群优化算法仿真结果如图3(b)所示。基本粒子群优化算法仿真结果如图3(c)所示。混合蛙跳优化算法仿真结果如图3(d)所示。 表3 四种优化算法单位飞行小时成本的仿真结果Tab.3 Simulation results of four optimization algorithms on cost per flight hour 从图3 中可以看出,在四种优化算法中,蛙跳退火粒子群优化算法能够有效地避免陷入局部最优的情况发生,方差最小,得到的结果为四种优化算法中最优,且结果分布较为稳定,其他三种优化算法所得最优解皆与蛙跳退火粒子群有较大差距,且结果分布较为分散,其中退火粒子群与基本粒子群的表现基本一致,混合蛙跳优化算法的结果较为集中,但最优解的取值较差。通过以上对比分析可得:蛙跳退火粒子群优化算法适用于本文所提出的问题,且对于复杂问题,蛙跳退火粒子群优化算法相较于其他智能算法有更好的表现,能够有效地避免局部最优解的出现。 图3 不同优化算法的Cefh仿真结果Fig.3 Cefhsimulation results of different optimization algorithms 在本文问题的已知条件中,发动机平均返厂时间间隔为x(i)∈(6 000,18 000)飞行小时,且发动机全寿命内预计飞行时间总和∑x(i) ∈(72 000,80 000),因此全寿命周期内最少返厂总次数为4次,总返厂次数4次会导致每次的平均返厂时间间隔皆为单次返厂时间间隔最大值18 000 飞行小时,由于此种极限情况在实际运行中出现的概率较小,因此不考虑此种情况。对发动机全寿命内总返厂次数5~8 次进行仿真模拟,分别计算单位飞行小时的维修成本和总的维修成本。考虑到智能算法的随机性,每种情况分别进行50 次模拟,取其中最佳结果为该种情况的仿真结果,发动机全寿命内总返厂次数5~8次单位飞行小时维修成本和总维修成本如表4所示,发动机四种不同维修方案的返厂次数的平均返厂送修时间间隔如表5所示。 以某发动机全寿命内送修方案为例,给出了四种不同的维修方案。计算四个维修案例单位飞行小时的维修成本,分别是方案1 为322.459 8 $,方案2 为348.005 1 $,方案3 为376.801 2 $,方案4为405.961 8 $。方案1单位飞行小时的维修成本最低,方案4最高。 表4 发动机全寿命内总返厂次数5~8次的单位飞行小时维修成本和总维修成本Tab.4 Total and per flight hour maintenance costs of engine with 5-8 total return times in full life time 表5 四种维修方案的平均返厂送修时间间隔 单位:飞行小时Tab.5 Mean return to shop visit time intervals of four different maintenance schemes unit:flight hour 由仿真结果可见,返厂次数与单位小时维修成本为正相关,随着返厂次数的增加,单位小时维修成本也相应增加,且增加量变化不大,可认为返厂次数与单位小时维修成本成线性关系,发动机返厂次数与单位飞行小时维修成本的关系如图4 所示。且返厂次数与总成本亦为正相关,发动机返厂次数与总维修成本的关系如图5 所示。因此可以得到结论:从经济性角度考虑,发动机返厂次数越少,所需的维修总成本和单位小时维修成本越低。 图4 发动机返厂送修次数与单位飞行小时维修成本的关系Fig.4 Relationship between number of return to shop visit and maintenance cost per flight hour of engine 图5 发动机返厂送修次数与总维修成本的关系Fig.5 Relationship between number of return to shop visit and total maintenance cost of engine 但在选择维修方案时,除了考虑低的单位飞行小时维修成本这一方面,还要考虑发动机在翼的性能风险,即可靠性,在此仅通过单元体大修时在翼累积的飞行小时数与其软时限的对比值来分析。以发动机全寿命周期内共5 次返厂为例,通过获得单位飞行小时的最优维修成本Cefh确定各单元体的修理级别及自上次深度修理累积工作时间(Time Since Heavy Maintenance,TSHM)与单元体软时限(Soft time)的比值,结果如表6所示。发动机全寿命周期内5~8次返厂四种维修方案中,冷端和热端部件自上次深度修理或自新的累积工作时间TSN(Time Since New)与单元体软时限比值的最大值,如表7所示。 表6 发动机5次返厂的不同单元体修理级别及自上次深度修理后的累积工作时间与单元体软时限的比值Tab.6 Maintenance level of different engine modules after 5 returns and ratio of accumulated working time since heavy maintenance and module soft time 表7 四种维修方案冷端和热端部件TSHM(TSN)/Soft timeTab.7 TSHM(TSN)/Soft time of cold section and hot section parts of four different maintenance schemes 发动机全寿命内返厂5 次时,从可靠性角度来说,热端部件(燃烧室/扩压器,高压涡轮导向器,高压涡轮,低压涡轮)在第一次返厂送修时维修等级为深度修理,自新发累积工作飞行小时数与软时限的比值为112.49%,第二次返厂和第三次返厂送修时维修深度为深度修理,自上次深度修理累积工作飞行小时数与软时限的比值分别为112.49%和112.5%,均在软时限上限的允许范围内。在第三次返厂时含有限寿件的单元体更换限寿件,限寿件自新件累积工作时间为53 996 个飞行小时。高压压气机在第二次返厂送修时,自新发累积工作飞行小时数与软时限的比值为119.99%,除此以外,冷端部件自新TSN/上次深度修理累积工作飞行小时数均未超过软时限。 发动机返厂6 次时,热端部件在第四次和第五次返厂送修时维修深度为深度修理,自上次深度修理累积工作飞行小时数与软时限的比值分别为112.4%和112.39%,均在软时限上限的允许范围内。在第四次返厂时含有限寿件的单元体更换限寿件,限寿件自新件累积工作时间为50 814个飞行小时。低压压气机、风扇机匣和中介机匣在第二次返厂送修时,自新发累积工作飞行小时数与软时限的比值为129.195%,第四次返厂时自上次深度修理累积工作飞行小时数与软时限的比值为124.875%,高压压气机自新/上次深度修理累积在翼时间均没有超过软时限。 发动机返厂7 次时,热端部件在第三次和第四次返厂送修时自上次深度修理累积工作飞行小时数与软时限的比值分别为112.71%和112.41%,均在软时限上限的允许范围内。在第四次返厂时含有限寿件的单元体更换限寿件,限寿件自新件累积工作时间为51 970 个飞行小时。低压压气机、风扇机匣和中介机匣在第二次返厂送修时,自新发累积工作飞行小时数与软时限的比值为129.955%,第四次返厂时自上次深度修理累积工作飞行小时数与软时限的比值为129.895%,高压压气机自新/上次深度修理累积在翼时间均没有超过软时限。 发动机返厂8 次时,热端部件在第二次返厂送修时维修等级为深度修理,自新发累积工作飞行小时数与软时限的比值为119.83%,第四次返厂和第五次返厂送修时维修深度为深度修理,自上次深度修理累积工作飞行小时数与软时限的比值分别为119.9%和112.48%,均在软时限上限的允许范围内。风扇机匣、中介机匣和联轴器在第六次返厂送修时维修等级为深度修理,自上次深度修理累积工作飞行小时数与软时限的比值为124.69%,冷端部件自新/深度修理累积在翼时间均未超过软时限,在第五次返厂时更换限寿件,限寿件自新累积工作时间为56 358飞行小时。 本文研究依据维修指导手册中的各单元体送修逻辑图,考虑限寿件到寿更换的情况,构建发动机送修成本函数,借助智能算法建立模型在保证可靠性和安全性前提下优化送修成本,确定各单元体修理级别并进行可靠性分析,可以得到以下一些结论: 1)全寿命周期内发动机单元体维修等级决策判断逻辑及送修成本模型较为复杂,通过算例与基本粒子群优化算法、退火粒子群优化算法、混合蛙跳优化算法等进行求解对比,与其他三种优化算法相比本文模型成本最优,适用于民航发动机各单元体送修决策及维修成本控制问题,与工程实际较为接近,可为航空公司和大修企业提供发动机送修决策支持并且优化送修的经济性。 2)考虑到智能算法的随机性,蛙跳退火粒子群优化算法对发动机全寿命内总返厂次数5~8 次进行50 次仿真模拟,取其中最佳结果为该种情况的单位飞行小时维修成本和总维修成本,可知返厂次数与单位小时维修成本为正相关。 3)以发动机全寿命周期内共5 次返厂为例,通过获得单位飞行小时的最优维修成本Cefh来确定各单元体的修理级别并计算自上次深度修理累积工作时间与单元体软时限的比值(TSHM/Soft time),同时分析5~8 次返厂时热端部件和冷端部件的可靠性。航空公司工程师在制定发动机全寿命的实际送修方案需从可靠性和维修成本两方面综合考虑,同时可以结合预期的在翼飞行时间和运营状况来考量。 本文研究仍然存在一定程度上的不足,如基于蛙跳退火粒子群优化算法的发动机单元体修理级别决策及成本优化仅考虑限寿件和单元体送修级别的影响;而在实际工程应用中,还需考虑发动机的在翼性能衰退情况、航线基地的维护报告、需返厂执行的服务通告、上次返厂的试车报告多种因素的影响。航空公司也可根据发动机机队实际运行情况来调整软时限的下限因子、上限因子和检查因子。发动机全寿命周期的多拆发影响因素的送修决策及成本控制是后续研究方向。

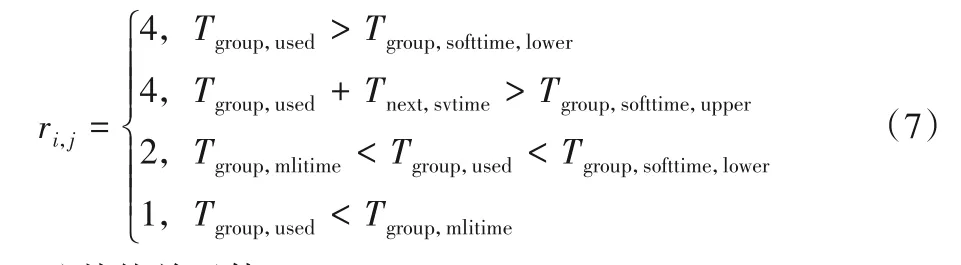
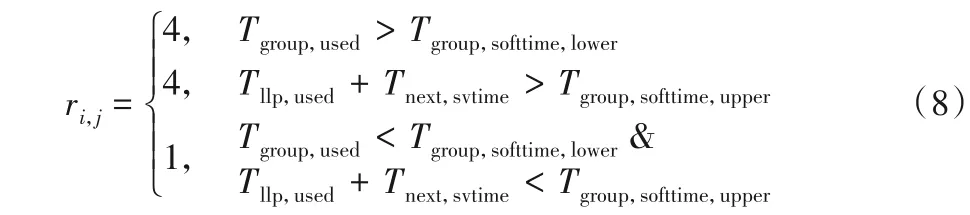
1.3 发动机送修成本


2 蛙跳退火粒子群优化算法
2.1 随机化初始解
2.2 退火蛙跳粒子群优化算法设计


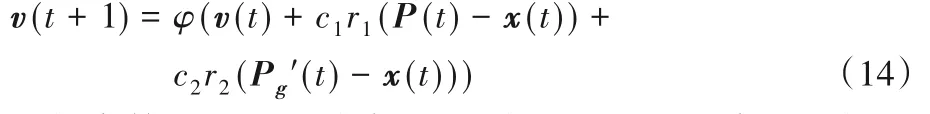
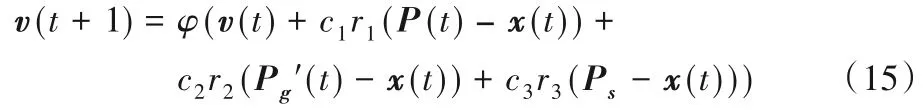

3 算例仿真及结果分析





4 结语

