改善环境光照对强反光体表面红外测温精度影响的补偿算法研究
魏绍亮,韩连伟,程奉玉
〈测量技术〉
改善环境光照对强反光体表面红外测温精度影响的补偿算法研究
魏绍亮,韩连伟,程奉玉
(河南理工大学,河南 焦作 454000)
针对铝业加工中的轧辊表面光滑,具有强反光特性,红外测温传感器测温易受环境光照影响,致使轧辊表面测温精度低,影响冷却控制系统对轧辊表面降温处理精度,进而造成产品质量差的现象,本文提出并构建了一种基于光照强度的红外测量温度补偿算法,以提高环境光照对强反光体表面温度测量的精度。实验结果证明本方法能较好地弥补光照强度变化对红外温度测量产生的测量误差,提高了测量精度。该补偿算法运算简单、适应性强,为改善光照强度变化对测量精度的影响提供了新的方法。
强反光体;红外温度传感器;测温精度;光照强度;补偿算法
0 引言
精确测量温度是工业、农业、仓储、环境监测等领域中重要的基本数据之一,有利于安全生产、提高产品质量和生产效率等。由于工业生产所处的环境以及空间的复杂性使得传统的接触式测温方式无法满足测温要求,对非接触、远距离测温技术的需求越来越大。红外测温传感器具有测温范围大、无热惯性、响应速度较快的优点,满足众多场合对温度测量范围和精度的要求,在现代工业生产、科学研究等领域得到越来越广泛的应用[1-3]。
铝是国民经济中重要的基础原材料,广泛用于建筑、包装、交通运输、电力等领域。铝制品生产离不开轧辊的作用,铝业加工中的轧辊表面光滑,具有强反光特性,属于直线光轴类的辊状体。在带材轧制过程中,轧件的热量以及轧件受到挤压变形所释放的热量都将使轧辊的温度升高,并沿其轴向方向产生热凸度,进而影响带材的加工质量。轧辊由于表面反复受到来自带材的急热和冷却液造成的急冷,极易产生疲劳破坏,从而发生生产事故[4-5]。因此,在铝板材轧制过程中实时监测轧辊表面温度分布情况是对轧辊表面温度精确控制的重要先决条件。国内外相关研究文献表明[5-11],目前研究者主要集中在研究红外温度传感器对物体表面进行温度测量的方法及物体表面发射率、测量距离等因素对测温精度的影响原因,而关于环境光照对强反光体表面温度测量精度影响的研究文献较少。本文从红外测温原理出发,通过实验揭示了不同光照强度对强反光体表面温度测量精度产生的影响,并对实验结果进行分析研究,进而建立强反光体基于不同光照强度的红外测温补偿算法,提高强反光体表面测温精度。
1 红外测温原理
自然界中,任何物质内部的带电粒子都是处于不断运动的状态。当物体温度高于热力学温度0K(摄氏温度-273.15℃)时,物体就会不停地向外辐射红外能量[6]。物体向外辐射的红外能量大小与波长和物体温度有关,因此可以通过测量物体向外辐射的红外能量,进而得到物体表面温度的精确值,这就是红外测温的基本原理[7-8]。
黑体辐射理论指出理想状态下可以把辐射物体看作一个黑体。它吸收的能量不能反射、折射等,全部辐射出来。普朗克定律揭示了黑体辐射能量在不同温度条件下按其波长分布的规律[9]。其数学表达式为:
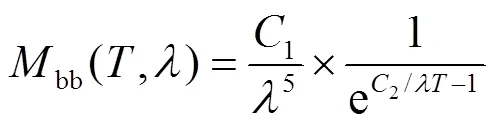
式中:bb(,)为黑体辐射能量密度,W/(mm×m2);1为第一辐射常数,1=2p2=(3.7415±0.0003)×10-16W×m2;2为第二辐射常数;2=/=(1.43879±0.00019)×10-2m×K;为光波的辐射波长,mm。
在任何温度下,能全部吸收投射到其表面上的任意波长辐射能的物体称为绝对黑体。绝对黑体的吸收系数为1,而反射系数为0,除按一定要求设计的腔体近似为黑体外,绝对黑体在自然界是不存在的。所有物体的表面反射系数都小于1,称之为灰体。灰体的红外辐射度一般都不直接测量,而是通过与同温度下的黑体辐射度的比值来表示[10]。比较实测物体与黑体在各个温度、波长的法向辐射度的关系,可以得到如下关系式:
=(,)×bb(2)
式中:是实际接收到的辐射度;为发射率,是关于温度和波长的函数,绝大多数热辐射物体发射率是随着波长的变化而缓慢变化的,具有较强的鲁棒性,因此一般可以把发射率看作常数。
根据斯特藩-玻尔兹曼定律:
bb=×4(3)
式中:为斯特藩-玻尔兹曼常数,=5.67032×10-8(W×m-2×K-4);为物体的热力学温度。
该定律指出,黑体的辐射度正比于它的热力学温度的四次方。这一结论不仅对黑体是正确的,而且对于任何实际物体也是成立的。实测热辐射物体的辐射度为:
=()4(4)
式中:()为温度为时全波长范围的材料发射率,也称之为黑度系数。式(4)为辐射式温度计测温提供了理论依据。
由红外测温原理及实际情况可知,在实际环境中实测物体除了自身红外能量辐射外,还有其他形式的辐射能量,不同温度的物体之间不断进行辐射能量交换,即处在辐射热平衡状态[11-12]。对实际物体进行表面温度测量时,物体辐射的能量不仅仅来自于物体自身,同时也会包括来自环境光照射温度的能量,这部分能量照射在物体表面再经过反射也会被红外测温系统接收,影响到测量结果的准确性。除此以外还会有某些能量通过被测物体透射进入红外测温系统并被接收,进一步影响测温结果的准确性[13-14]。本实验中使用的样品光轴具有良好的无透射纹理,在实验中忽略透射能量影响。
本文主要探讨环境光照强度对红外测温传感器测量精度的影响规律,建立光照强度变化与温度之间的数学模型,构建补偿算法补偿环境光照产生的测温误差。
2 实验测试与结果分析
铝板材加工设备中的轧辊具有表面光滑、强反光等特性,而且质地细密、无透射性,本实验选择反光性能较好的铝合金棒材作为测量目标进行实验。根据红外传感器工作参数和铝板材实际生产设备现场工况搭建试验系统,合金棒材通过轴承固定在一定高度的固定支架上,红外传感器安装在距离棒材500mm的另一支架上。为了保证实验研究的数据可靠,不受其他环境光照因素的影响,本研究测试实验均在河南理工大学精密工程研究所进行,在研究所内设计了一个独立密闭空间,周边做了消除反光处理,并设计了光源安装支架,通过改变光源,探寻红外传感器测温精度随光源光强变化的规律。实验过程中保持红外入射角度为0,改变环境光照强度开展测试实验。具体测试环境如图1所示,图中(a)图是弱光源实验,图(b)是强光源实验。
2.1 黑暗无光(光照强度为2lx)条件下的测试实验
选用带有IS(infrared scanner)激光瞄准的红外传感器,铝合金棒材的发射率为0.02~0.1。通过对固定点的反复测量,确定测量对象铝合金棒材的发射率为0.058,此时的误差在1℃以内,具体测试结果如图2所示。

图1 实验测试环境
图2中轴代表实际温度,轴代表红外传感器的测量温度。由图2可知测量曲线相对比较平滑,无极端值,与=曲线(即实际温度与测量温度相等)基本吻合,红外温度传感器测得的温度数值与实际温度值之差不超过1℃,且大部分误差都在0.6℃以下,满足了测温误差的要求。
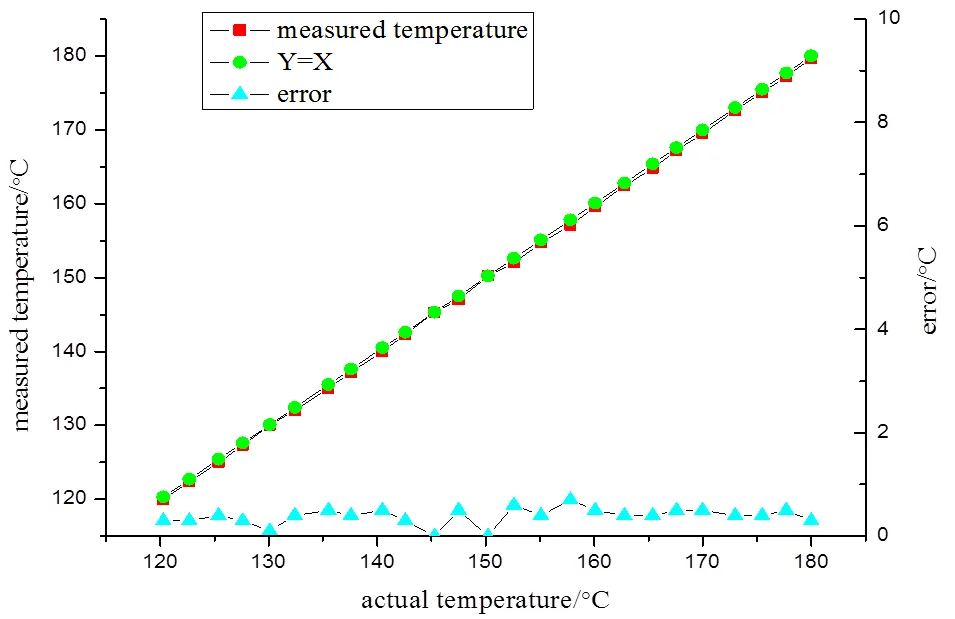
图2 光照强度为2lx时的红外测温结果
2.2 不同光照强度下红外传感器的温度测量
通过上述实验可以确定所选用的铝合金棒,其发射率为0.058。在实验中固定其发射率并保证测量对象温度恒定,通过改变铝合金棒材表面的光照强度进行实验。实验中选取棒材的固定温度分别为:130℃、140℃、150℃、160℃、170℃和180℃,同时选择的光照强度分别为:50lx、60lx、70lx、80lx、90lx、100lx、110lx、120lx、130lx,测量结果如图3(a)~(f)所示。
图中红色曲线代表棒材的实际温度,绿色曲线代表红外温度传感器的测量结果,蓝色曲线是误差曲线。通过观察图3可以发现,当棒材表面温度分别为130℃、140℃、150℃、160℃、170℃和180℃时,在9个不同光照强度情况下,红外温度传感器所测量的棒材样本的温度数据也是不同的。当棒材表面的光照强度不同时,其测量结果均高于实际温度,且随着光照强度的增大,测量误差越来越大。因此,在用红外温度传感器对具有强反光特性的棒材进行温度测量时,测量结果总是正向偏离真实值,且随着光照强度的增大,正向偏离程度逐渐增大。
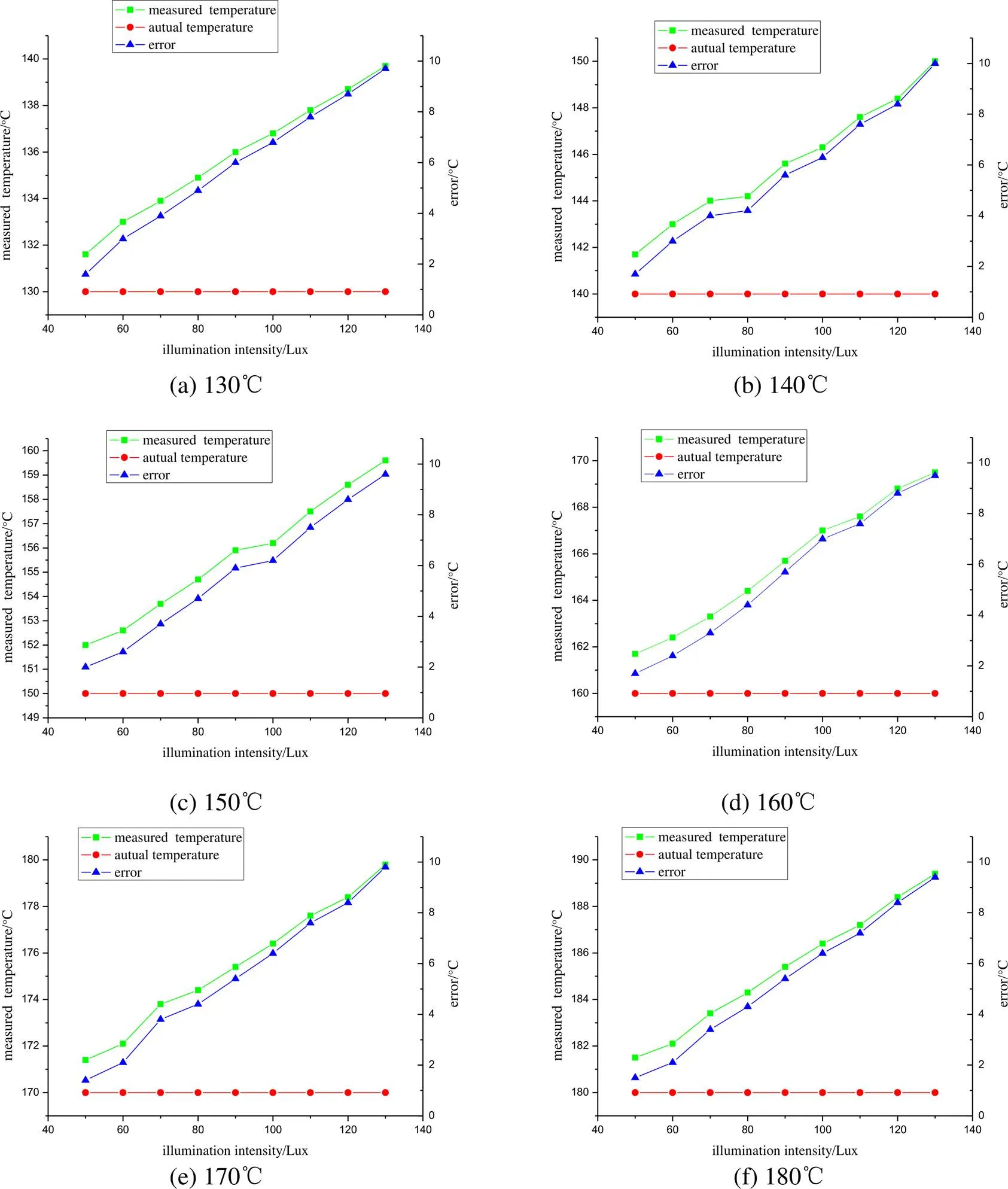
图3 不同温度下不同光照强度时的测量结果与误差
3 不同光照强度下的红外测量补偿算法
根据斯特藩-玻尔兹曼定律,假设变量为待测物体表面光照强度的函数,记为()。函数()定义为光照强度的补偿因子,则斯特藩-玻尔兹曼公式可表示为:
M=()×()4(5)
式中:M是被测物体在光照强度为时的辐射量,红外温度传感器所接收的红外波长为1.6mm,且()为常数,公式(5)可转化为:
M=()×4(6)
式中:是一个常量,它是在特定条件下获得的特定值,其值由()和确定,=()×将函数关系与温度变化结合可以得到公式(7):
M=×(L()×)4(7)
式中:L()是温度与光照强度有关的系数。将辐射量的变化通过温度来反映,则不同光照强度条件下红外温度传感器测得的温度T为:
T=L()×(8)
由图3可知,红外温度传感器测得的温度值随被测物体表面光照强度的变化而变化,分析同一温度下不同光照强度条件下的测量结果,确定L(),并初步证实了L()的变化。为了进一步揭示L()的变化规律,在实验中对连续变化的温度进行实时测量,具体测量结果如图4所示。
图4中,10条曲线分别对应10种不同光照强度条件下的测量结果,即2lx、50lx、60lx、70lx、80lx、90lx、100lx、110lx、120lx、130lx。横坐标表示被测量物体的真实温度,纵坐标表示红外温度传感器的实际测量温度。图中的红色曲线是参考曲线,它是被测对象在黑暗中(即光照强度为2lx)的标准温度曲线,而其他曲线均分布在红色曲线上方,因此,可以得知系数L()的取值大于1。通过比较参考曲线与另外9条温度曲线,可以发现随着光照强度的不断提高温度曲线在缓慢地向上移动,说明随着光照强度的增大实际测量值在不断地变大,误差在逐渐地增大。绝对误差分布如图5所示。
观察图5可知,绝对误差随着光照强度的增大而增大,而且每组数据相对稳定,但也出现了个别突变情况,分析可得,产生突变的原因主要由以下因素造成:
1)表面热电偶在对实验样本进行测量时发生滑动,导致热平衡被打破;
2)测试过程中热电偶和红外温度传感器对温度变化的反应时间不同,导致测量结果产生不同。
考虑到工程测试的精度要求,选择采用构造补偿公式的方法来减小测量误差。通过观察图4的数据分布可以发现,不同光照强度条件下的红外温度测量结果之间存在线性关系,所以可以通过最小二乘法拟合出补偿算法。
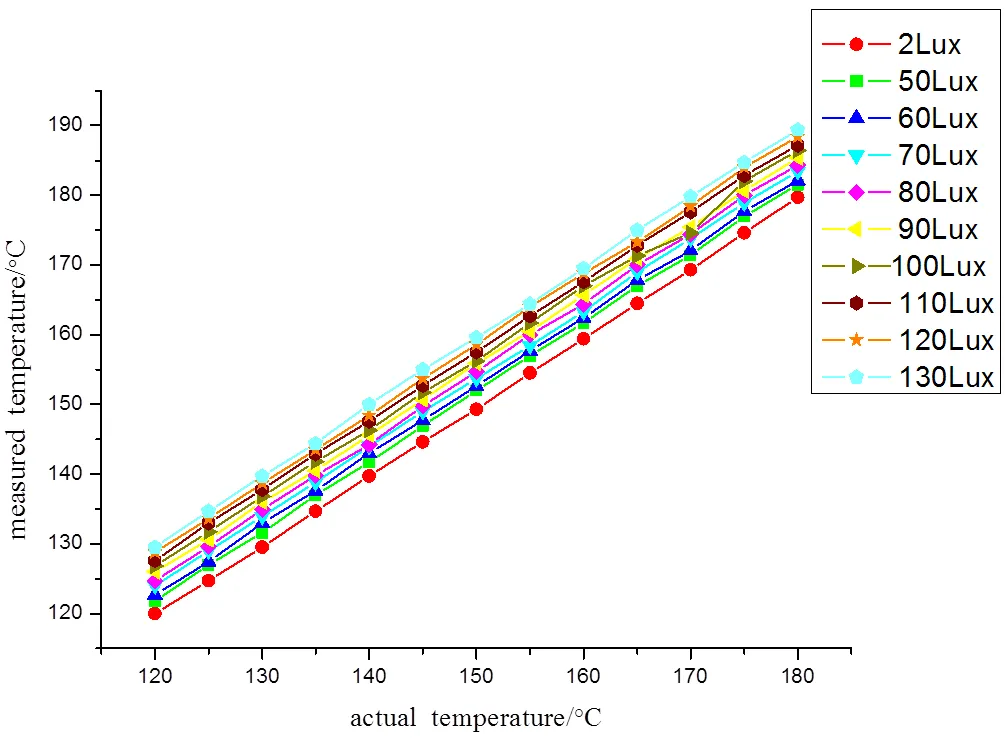
图4 不同光照强度条件下实际温度与测量温度比较
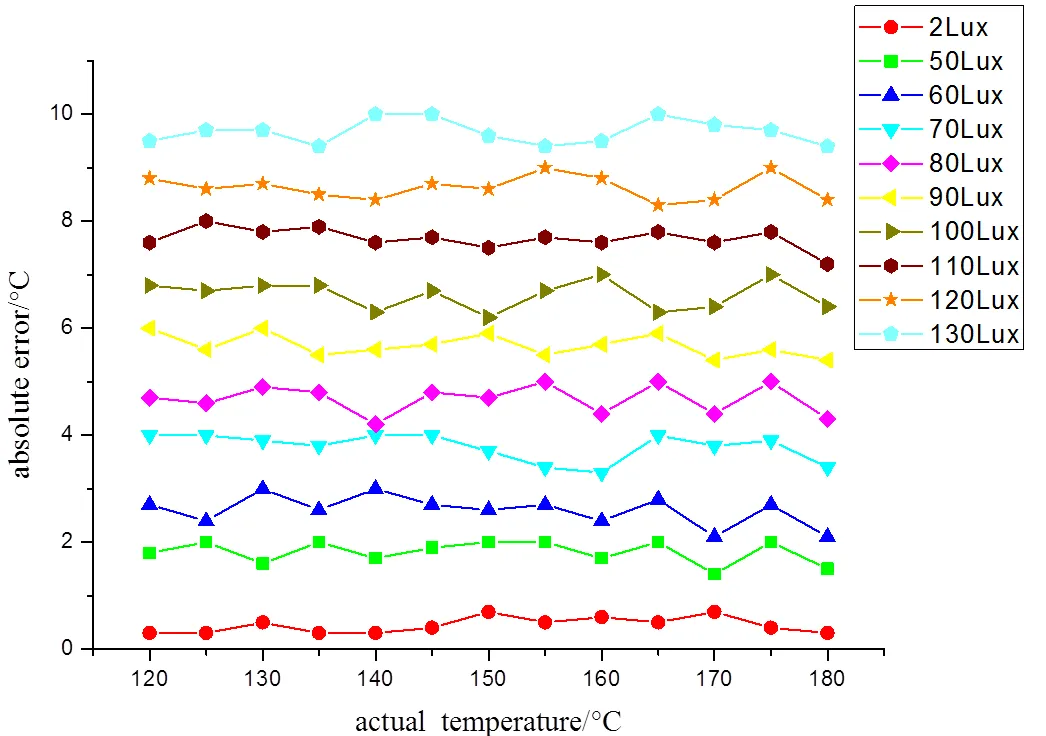
图5 不同光照强度下测量温度的绝对误差
由图4和图5实验数据拟合出几组不同光照强度下红外温度测量结果的补偿公式:
50lx:E=1.0029-2.746
60lx:E=1.0042-3.6777
70lx:E=1.0046-4.8873
80lx:E=1.0047-5.6099
90lx:E=1.0052-6.4880 (9)
100lx:E=1.0065-7.7009
110lx:E=1.0068-8.6374
120lx:E=1.0071-9.8010
130lx:E=1.0084-10.9972
由公式(9)可知,各个补偿公式中的一次项系数的值均接近于1,故可构建关于光照强度的通用补偿公式:
b=E+() (10)
式中:b为补偿后的温度值;()是与被测对象表面光照强度有关的函数关系式,分析公式(9)中的补偿公式,做出补偿系数散点图,发现其呈线性关系。如图6所示。
应用最小二乘法进行曲线拟合,构建出不同光照强度情况下,红外温度传感器测量结果的通用补偿算法公式为:
b=E+(6.0838-5)×+1.0001 (11)
为了验证补偿公式的正确性,根据公式(11)对不同转速的实际测量结果进行补偿修正,修正结果如图7所示。
图7中,10条曲线分别代表10种不同光照强度情况下使用补偿公式对测量结果的修正曲线,横坐标代表被测样本的实际温度,纵坐标代表补偿后的温度。比较图7与图4可知,补偿算法修正后的测量数据与实际温度基本一致,表明本实验构建的补偿算法可以有效地提高强反光体在不同光照强度下的红外测温精度与稳定性。
4 结论
本文基于斯特藩-玻尔兹曼定律和普朗克定律,结合实验和数据分析,深入分析了红外测温的原理,同时改变环境光照强度对强反光物体的表面温度进行测量,并系统分析了测量数据,构建了基于斯特藩-玻尔兹曼定律的红外补偿算法,并得出如下结论:
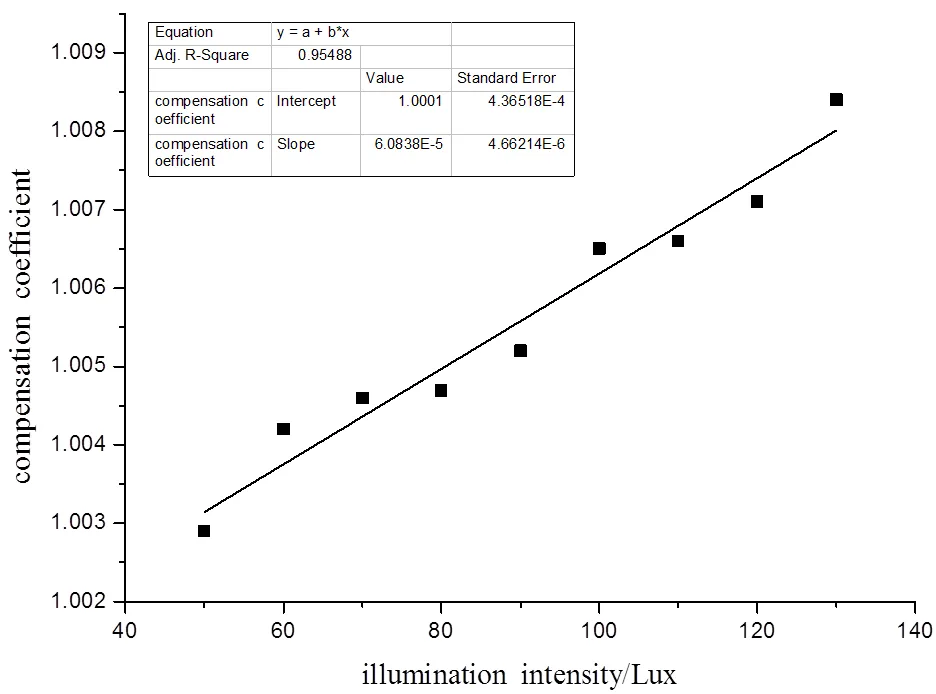
图6 补偿系数与光照强度的关系图
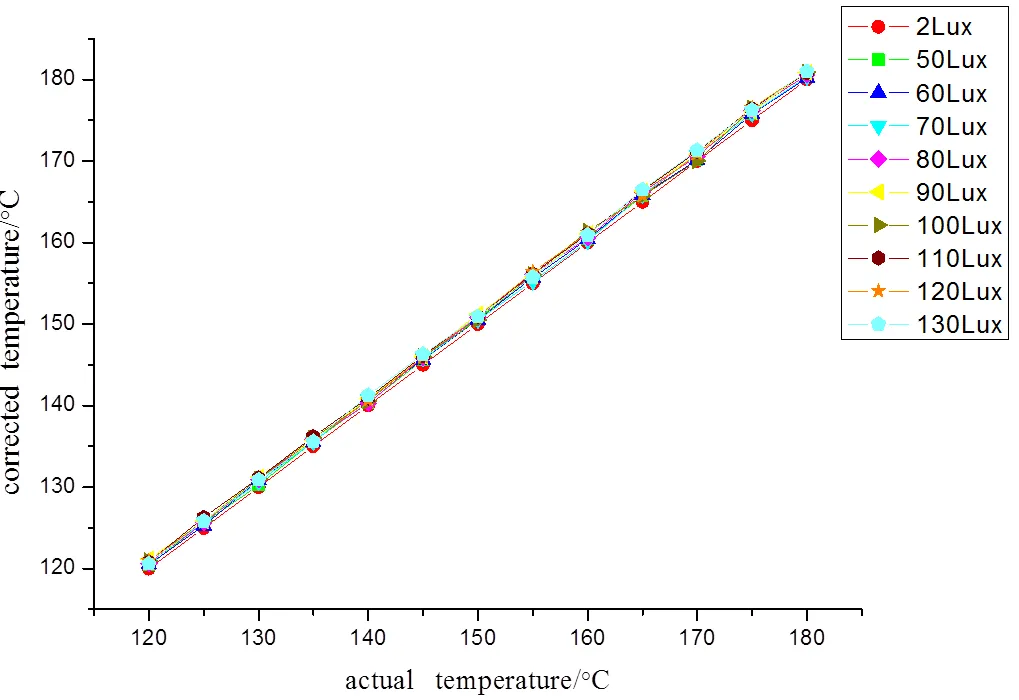
图7 补偿算法修正后的温度分布曲线
1)当被测物体表面光照强度发生变化时,其表面红外温度测量值会随之发生变化,光照强度越强,测量误差越大,测量值向上偏离真实值。
2)基于光照强度所构建的红外温度测量补偿公式降低了强反光体表面光照强度变化对红外测量精度的影响,提高了强反光体表面温度测量的精度。
[1] Lucchi Elena. Applications of the infrared thermography in the energy audit of buildings: a review[J]., 2018, 82: 3077-3090.
[2] Manara J, Zipf M, Stark T, et al. Long wavelength infrared radiation thermometry for non-contact temperature measurements in gas turbines[J].,, 2017, 80: 120 -130.
[3] ZHANG C, Gauthier E, Pocheau C, et al. Surface temperature measurement of the plasma facing components with the multi-spectral infrared thermography diagnostics in tokamaks[J]., 2017, 81: 215-222.
[4] Atas Berksoy, Bag Ozlem, Yazici Selcuk, et al. Use of noncontact thermography to measure temperature in children in a triage room[J]., 2018, 97(5): e9737.
[5] Rubén Usamentiaga, Daniel Fernando García. Infrared thermography sensor for temperature and speed measurement of moving material[J]., 2017, 17: 2-21.
[6] SONG B Q, XIN Y E, YANG D J, et al. Precise measurement of voltages in space cryogenic radiation temperature system[J]., 2015, 23(7): 1903-1910.
[7] Masoudi S, Gholami M A, Janghorban Iariche M, et al. Infrared temperature measurement and increasing infrared measurement accuracy in the context of machining process[J]., 2017, 12(4): 353-362.
[8] SONG B Q, XIN Y E, YANG D J, et al. Precise measurement of voltages in space cryogenic radiation temperature system[J]., 2015, 23(7): 1903-1910.
[9] 陈文亮, 胡毓国, 李杏华, 等. 回转体测量机温度误差分析及补偿[J]. 纳米技术与精密工程, 2015, 13(1): 22-27.
CHEN Wenliang, HU Yuguo, LI Xinghua, et al. Analysis and compensation of temperature error of rotary measuring machine[J]., 2015, 13(1): 22-27.
[10] 孟凡伟, 高悦, 马翠红, 等. 基于热辐射理论的熔融金属红外测温模型研究[J]. 红外技术, 2017, 39(8): 766-771.
MENG Fanwei, GAO Yue, MA Cuihong, et al. Infrared temperature measurement model for molten metal based on thermal radiation theory[J]., 2017, 39(8): 766-771.
[11] 廖盼盼, 张佳民. 红外测温精度的影响因素及补偿方法的研究[J]. 红外技术, 2017, 39(2): 173-177.
LIAO Panpan, ZHANG Jiamin. Research on influence factors for measuring and method of correction in infrared thermometer[J]., 2017, 39(2): 173-177.
[12] 石东平, 吴超, 李孜军, 等. 基于反射温度补偿及入射温度补偿的红外测温影响分析[J]. 红外与激光工程, 2015, 44(8): 2321-2326.
SHI Dongping, WU Chao, LI Zijun, et al. Influence analysis of infrared temperature measurement based on reflection temperature compensation and incident temperature compensation[J]., 2015, 44(8): 2321-2326.
[13] 田昌会, 杨百愚, 蔡明, 等. 大气背景对红外目标探测的影响[J]. 红外与激光工程, 2014, 43(2): 439-441.
TIAN Changhui, YANG Baiyu, CAI Ming, et al. Influence of atmospheric background on infrared target detection[J].g, 2014, 43(2): 439-441.
[14] 刘纯红, 吴海滨, 熊丹枫, 等. 热辐射测温系统中探测器非线性校正方法[J]. 量子电子学报, 2017, 349(2): 227-230.
LIU Chunhong, WU Haibin, XIONG Danfeng, et al. Nonlinear calibration method of detector in thermal radiation temperature measurement system[J]., 2017, 349(2): 227-230.
Compensation Algorithm to Improve the Influence of Ambient Light on the Infrared Temperature Measurement Accuracy of a Strong Reflector Surface
WEI Shaoliang,HAN Lianwei,CHENG Fengyu
(Henan Polytechnic University, Jiaozuo 454000, China)
A roll surface in aluminum processing is smooth, has strong reflective characteristics, and is easily affected by ambient light when using an infrared temperature sensor to measure the temperature, resulting in low temperature measurement accuracy on the roll surface. The cooling control system affects the precision of cooling treatment on the roll surface, resulting in poor product quality. In this study, an infrared temperature compensation algorithm based on light intensity is proposed and constructed to improve the accuracy of ambient light measurement of the surface temperature of a strong reflector. Experimental results show that this method can compensate for measurement errors caused by changes in illumination intensity, thereby improving the measurement accuracy. The algorithm is simple and adaptable and provides a new approach to strengthening the accuracy of temperature measurement given speed change.
strong reflector, infrared temperature sensor, accuracy of temperature measurement, illumination intensity, compensation algorithm
TH701
A
1001-8891(2020)12-1179-06
2020-02-20;
2020-03-17.
魏绍亮(1969-),男,博士,教授。主要研究方向:机电测试与控制、智能仪表设计、信号传输与处理。E-mail:wsl_ify@163.com。
河南理工大学博士基金(B2016-29)。

