近十年上海蔬菜价格的SARIMA 分析与预测

郑秀国,杨 娟,钱婷婷,许叶颖

(上海市农业科学院农业科技信息研究所,上海数字农业工程技术研究中心,上海201403)

蔬菜是“菜篮子工程”的主要产品之一,蔬菜产业也是城市近郊农业生产者的重要经济来源。 然而,蔬菜价格不仅受到市场供求、自然气候、生产成本、市场流通等规律性因素的影响,还会受到突发的气候变化、供求变化等影响,尤其是近年来大市场大流通下蔬菜供应的季节性或种类性不均衡时有发生,导致蔬菜价格波动频繁。

作为生物性产品,蔬菜的供应受季节气候的影响最大,其价格随着供应的周期性波动而波动,在时间序列上表现出明显的季节性和周期性特征,时间序列模型可较好地反映这种变化特征。 常用于农产品价格分析的时间序列模型有自回归移动平均模型(ARIMA 模型)、季节自回归移动平均模型(SARIMA 模型)和Holt-Winters 指数平滑模型(Holt-Winters 模型)等,其中SARIMA 模型、Holt-Winters 模型均考虑到季节性因素的影响[1]。 SARIMA 模型在农产品价格分析预测中应用十分广泛,如陈灿煌等[2]、陈兆荣等[3]运用该模型预测了中国农产品价格指数,王云鹏[4]用其预测农业生产资料价格指数。 应用该模型预测农产品价格、蔬菜价格和单种类蔬菜价格也都取得了较好的效果[5-7],也是鸡蛋价格、肉鸡价格、生猪价格、猪肉价格常用的分析预测方法[8-11]。 李干琼等[12]采用5 种短期预测模型预测2009 年西红柿价格,表明SARIMA 模型明显优于其他4 种模型。 王美凤等[13]对4 种上海青菜价格预测模型进行了比较研究,表明SARIMA 模型的预测效果最好。 蔬菜价格是同期多种单种类菜价的汇总,开展蔬菜价格波动特征分析和预测研究,可为管理部门的政策调控和生产者的经营决策提供参考,对于减少蔬菜价格大幅波动对市民生活和蔬菜生产者的影响具有重要意义,然而尚未见蔬菜总体价格的波动特征与预测分析研究的报道。 为此,本研究采用2010 年1 月—2019 年12 月上海蔬菜批发价数据,建立上海蔬菜SARIMA 模型,进而对2020 年1—6 月上海蔬菜价格进行预测,通过模型预测效果分析进一步验证模型效果,最后根据SARIMA 模型参数值分析上海蔬菜价格波动特征。

1 数据来源与模型方法

1.1 数据来源

本研究所使用的数据序列为2010 年1 月至2020 年6 月上海蔬菜批发市场平均价格(元人民币∕kg,下同),记为PR,来源于上海市农产品价格监测与分析预测系统。 其中2010 年1 月—2019 年12 月数据用于上海蔬菜SARIMA 模型建立,2020 年1—6 月数据用于进一步验证分析模型预测效果。

1.2 建模方法

SARIMA(p,d,q)(P,D,Q)模型结构中,p 为自回归项数,q 为移动平均项数,d 为差分次数,P 是季节自回归阶数,Q 是季节移动平均阶数,D 为季节差分次数。 具有季节性、趋势性和周期性的平稳数据序列{Bt,t=1,2,…},可以采用SARIMA(p,d,q)(P,D,Q)模型结构建立模型。

首先对上海蔬菜批发价数据序列进行季节性、趋势性检验。 季节性检验通常采用时间序列趋势图来判断,若趋势图是以年为周期变动,则时间序列具有季节变动特征。 趋势性检验是采用CensusX-12 乘法方法对数据序列进行季节调整分解,获得季节调整后的趋势循环序列,再运用H-P 滤波法对获得的趋势循环序列进行趋势波动与循环波动序列分离,分离出的趋势波动图可观察出序列的变化趋势。

SARIMA 模型的建立与应用可通过Eviews 软件实现,主要过程如下:

1)序列平稳性检验。 可通过ADF 单位根检验来判断,对于非平稳时间序列,可以通过数据变换和差分实现序列的平稳化,并采用时间序列的自相关函数(ACF)和偏相关函数(PACF)是否截尾来判定序列的平稳性。

2)模型的识别。 主要通过观察序列的自相关函数(ACF)和偏相关函数(PACF)对可能的p,d,q 和P,D,Q 的参数值进行估计,由此构成不同的SARIMA 模型结构形式。

3)模型的参数估计。 运用最小二乘法估计模型的系数,并对其显著性进行检验。 对于不同参数模型的选优可采用BIC(贝叶斯信息)准则等综合判断。 最后,对选出的模型检验其残差是否为白噪声,一个适合的模型的残差序列应是白噪声过程,其ACF 和PACF 不应与0 有显著性差异。

4)模型预测。 由上述过程确定模型的最终参数后,即可得到模型,使用模型进行预测。

2 结果与分析

2.1 序列平稳化

从图1 可以看出,上海蔬菜价格表现出较明显的季节性,每年3 月至次年3 月蔬菜价格呈“W”型波动规律,价格高点多出现在3 月和9 月,价格低点多出现在6 月和11 月,数据在周期内呈现整体递增趋势,为非平稳序列。

首先,为消除序列可能存在的异方差,将原始序列进行对数化处理;其次,为消除趋势性,对原始序列进行季节性差分和普通一阶差分。 由图2 可以看出,处理后序列ΔΔ12LnPR 的自相关函数ACF 和偏相关函数PACF 整体呈现截尾态势,由此认为ΔΔ12LnPR 是平稳的序列。

2.2 模型建立与参数识别

本研究选择多种不同的模型进行拟合,如SARIMA(0,1,1) ×(1,1,1)12、SARIMA(2,1,1) ×(1,1,1)12、SARIMA(2,1,1) ×(1,1,2)12、SARIMA(2,1,2) ×(2,1,1)12、SARIMA(2,1,2) ×(2,1,2)12等p、q 和P、Q为3 以内的各种取值组合,发现SARIMA(3,1,3) ×(2,1,0)12参数显著性t检验结果最好。 从表1 可以看出,该模型结构各参数的相伴概率均小于0.15,确定上海蔬菜模型结构为SARIMA(3,1,3) ×(2,1,0)12。模型结构为:(1 -φ1B-φ2B-φ3B)(1 -Φ1B12-Φ1B24)Δ1Δ112logPr=(1 -θ1B-θ2B-θ3B)εtεt-N(0,0.100)。

回归方程的决定系统为0.71,误差项的方差估计值为0.100,模型中各参数的取值见表1。 模型的残差序列经检验为平稳的白噪声序列。

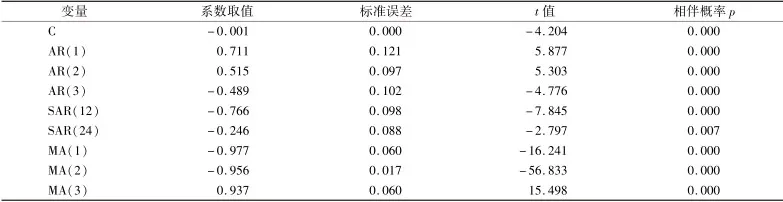
表1 SARIMA 模型参数估计与相关检验结果Table 1 Model parameter estimation and test results based on SARIMA model

2.3 模型预测

根据建立的SARIMA(3,1,3) ×(2,1,0)12模型对2020 年1—6 月的上海蔬菜价格进行静态预测和动态预测,通过实际价格和预测价格的比较,判断模型的预测精度。

市场调查发现,假期对蔬菜价格有一定影响,进一步分析了春节假期对蔬菜价格的影响。 从2010—2019 年上海蔬菜价格数据来看,含春节期间价格的1 月蔬菜月平均价格比不含春节期间价格的1 月上海蔬菜月平均价格低2.0%,含春节期间价格的2 月蔬菜月平均价格比剔除春节期间价格的2 月上海蔬菜月平均价格高12.3%,可见,春节假期对蔬菜价格影响效果不定。 但是春节当月的蔬菜价格整体高于其前后月份,如春节在1 月,1 月蔬菜价格比其前一个月和后一个月的价格平均高2.9%;春节在2 月,2 月蔬菜价格比其前一个月和后一个月的价格平均高7.7%。

为此,本研究在进行预测时考虑了假期效应,如果春节所在月份预测值高于前一个月预测值和后一个月预测值的平均值历史水平则不进行春节调整,反之则对春节所在月份的预测值进行相应调整——若春节在1 月,则1 月下调2.0%;若春节在2 月,则2 月上调12.3%。 如表2 所示,静态预测结果的平均误差为7.3%,动态预测结果的平均误差率为4.6%,上海蔬菜价格预测数据与实际数据基本一致。

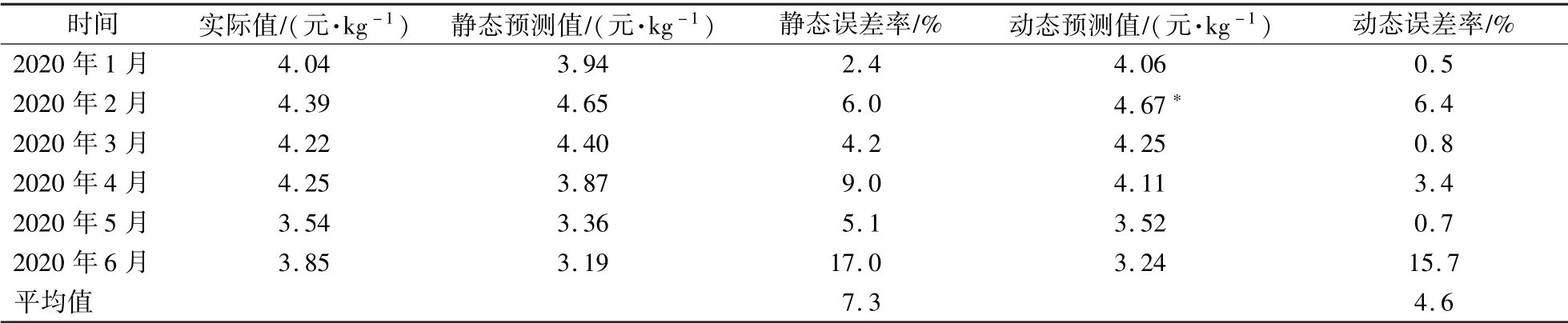
表2 上海蔬菜价格静态预测结果和动态预测结果Table 2 Static and dynamic prediction results of vegetable price in Shanghai

3 结论与讨论

研究结果表明,上海蔬菜价格具有较为明显的季节性和周期性特征,可用SARIMA 模型对上海蔬菜价格进行分析和预测。 根据模型的显著性检验和模型参数的显著性检验结果,SARIMA(3,1,3) ×(2,1,0)12模型效果最佳。 从模型参数值可以看出,上海蔬菜价格为非平稳序列,一阶差分序列为平稳序列;根据参数取值,可看出上海当月蔬菜价格不仅与其前3 个月的价格密切相关,而且受前2 年同月价格的影响。

上海蔬菜价格SARIMA(3,1,3) ×(2,1,0)12模型预测的上海蔬菜2020 年1—6 月批发价(经春节调整后)与实际价格的对比分析结果表明,模型静态预测的平均误差为7.3%,动态预测的平均误差为4.6%,实际应用中可结合2 种预测方式,达到更好的预测效果。 SARIMA(3,1,3) ×(2,1,0)12模型能较好地表现上海蔬菜价格的波动特征,可用于分析和预测上海蔬菜价格未来走势,指导产业发展。 但还要注意,时间序列模型建模主要依据历史价格所包含的信息,而实际影响市场价格波动的还有一些突发性因素,如台风暴雨、低温、暖冬等恶劣天气或者交通、疫情等突发事件,所以在实际价格的走势分析预测中,可在模型分析预测出规律性影响因素结果的基础上,再叠加考虑这些突发因素的影响,从而科学判断出各种影响因素对蔬菜价格影响的程度。