资源受限下的网络安全动态博弈模型
鄂小松, 石峻松
(1.树蛙信息科技(南京)有限公司,江苏 南京 210033)(2.南京信奥弢电子科技有限公司,江苏 南京 210039)
一般情况下,网络中攻防双方的对抗过程符合博弈论各项特征,因而可将博弈论引入解决攻防双方策略抉择问题。在实际对抗中,由于攻防双方知之甚少,因此在网络攻防冲突时会产生不完全信息问题。为有效解决不完全信息下的博弈问题,国内外学者进行了大量研究。Harsanyi[1]提出用贝叶斯纳什均衡解来解决静态博弈论中不完全信息问题。针对动态博弈论领域,通常的解决方法包括完美贝叶斯均衡[2]和序贯均衡[3]两种方法。对于有限动态不完全博弈过程,序贯均衡总能得到混合策略,然而对于完美贝叶斯均衡方法,其计算过程较为复杂。Nayyar等[4]在假设动态随机非零和博弈状态和观测方程是线性的且初始随机变量为高斯随机变量的前提下,利用求解线性方程组序列,提出了公共信息马尔科夫完美均衡计算方法。该方法的关键是将初始不完全信息下的博弈过程转化为一个完全信息下的虚拟博弈过程以及众多不同的或者更大的状态/动作空间。然而该方法无法对攻击者的策略集和效用函数进行差异性分析,且建模过程复杂。此外,为提高随机博弈过程状态观测及动作策略选取效率,Cole等[5]将具有惩罚函数的第三方观察者引入系统,且为每一个对抗参与者赋予私有信息观测状态。模型中每个参与者状态置信度仅依赖于当前状态而不依赖其策略,这种假设使得每个参与者当前策略选取受过去私有观测状态影响,严重时,策略选取将会产生较大偏差。
国内也有不少学者将博弈论引入网络信息安全领域。刘荣等[6]将信息安全中攻防冲突双方的收益进行量化,建立了对抗双方的博弈矩阵,同时将演化博弈理论引入冲突模型,求解攻防双方对抗过程中网络动态微分方程。在MATLAB中对网络攻防双方对抗过程进行了策略稳定性分析,通过5组均衡解验证了模型的准确性与有效性,然而在建模过程中假设攻防双方处于理想化背景,导致在计算对抗双方博弈冲突过程时,缺乏一定的现实基础。朱建明等[7]结合网络对抗攻防双方效能函数,基于系统动力学方程建立了不完全信息下具有自主学习机制的网络对抗演化博弈模型,并对模型进行了仿真,验证了引入第三方动态惩罚策略的非合作演化博弈过程纳什均衡的存在性与唯一性,然而建立模型过程中没有考虑计算资源受限情况。
综上,为了解决获取信息不完全以及计算资源受限情况下的网络安全问题,本文通过量化信息获取机制及资源受限条件,建立了网络安全中攻防双方动态博弈过程方程,并给出了纳什均衡及代价函数的计算过程。
1 博弈模型分析与建立
(1)
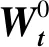
(2)
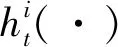
1.1 信息及策略选取模型
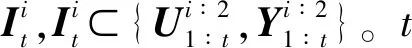
控制器的控制策略可表示为gi,定义为:
(3)

1.2 控制器资源限制模型
在博弈过程中,每一个控制器的可利用资源数量都具有一定限制,控制器i在t时执行的动作及策略选择不仅依赖于其他控制器的观测和响应动作,还需考虑自身资源消耗情况。
令控制器集合为J,t时公共信息的增量为Zt,有Zt=Ct/Ct-1。其中,Zt为增量集合, 则Zt={Z1,…,ZT}。因此,控制器i的资源限制条件可表达如下:
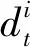
1.3 代价函数及纳什均衡
假定每一个控制器都存在一个代价函数,策略固定情况下,所有控制器的总代价函数可表达为:
(4)
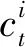
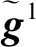
2 博弈模型计算过程
2.1 基本假设
为简化计算过程,对模型部分条件作如下假设:
假设1:假定系统中各个控制器获取的公共及私有信息随时间演化过程如下。
1)获取的公共信息Ct随着时间不断增加,即∀t∈T,Ct⊂Ct+1。令Zt+1=Ct+1/Ct为t到(t+1)时刻公共信息的增量,则Ct+1={Ct,Zt+1}。因此有:
(5)
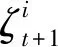
2)私有信息的演化过程可表达为:
(6)
式(5)表明,t到(t+1)时刻,增加的新公共信息一部分为t时刻选取的动作以及(t+1)时刻的观测集,另一部分为t时刻部分私有信息。式(6)表明控制器1和2私有信息的演化过程受到不同观察者及动作的影响。
在公共信息条件已知的条件下,任意时间t,控制器状态及私有信息的置信度的条件概率模型为:
(7)

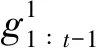
(8)
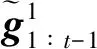
2.2 模型求解
根据假设2可知,Πt仅依赖于公共信息Ct,且由于任意参与者都能得到公共信息,因此对于所有参与者而言,Πt为已知的。因此Πt的演化可视为一个马尔科夫过程,记为
(9)
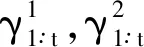
系统寻求纳什均衡问题最终简化为寻找Πt的马尔科夫完美均衡问题。下面将介绍贝叶斯博弈条件下一种改进的寻找马尔科夫完美均衡算法。
步骤1:初始T时刻,∀π∈Πt,状态xt的概率分布、动作集及其代价函数如下:
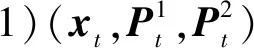
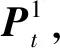
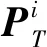
(10)
式中:Ui为控制器i(i=1,2)的动作集合;Zt+1为公共信息的增量;Mi为控制器的资源限制数量;j≠i,i,j=1,2。
步骤2:当t 图1所示为一个简化的火警网络控制模型,数据中心通过网络接收传感器搜集的环境信息,如空气湿度、烟雾浓度、温度、光照强度等。如果发现火灾,将产生警报信息并发送给控制器执行各类指令,如打开应急灯、关闭电梯、开启消防喷头等。 图1 简化的火警网络控制模型 (11) 此外,控制器1能够完全观测信息,控制器2观测误差率为1/3,则有 (12) 令各控制器资源上限Mi=1,且在一个时间步长后分享观测与动作集。在t时刻,公共信息与私有信息计算式如下: (13) (14) 式中:π(X2=1)为当X2=1时在分布下π的概率。 同理,当t=1时,δ1(x)=1-x,δ2(y)=1-y为博弈过程的贝叶斯纳什均衡。代价为: (15) 案例结果可为不完全信息、资源受限条件下博弈双方策略的选取提供借鉴。 进一步,令各控制器资源受限阈值Mi=25,系统噪声服从标准正态分布,各状态转移(信息演化)过程服从Sigmod函数,即: (16) 随着控制器增多,本文方法与Markov方法下的博弈过程中纳什均衡策略的最大执行策略数如图2所示。可以看出,随着系统控制器增多,两种方法下各控制器可获取资源不断增加,这种情况符合实际规律。本文方法由于考虑了资源受限情况,系统执行均满足资源受限要求,然而Markov方法存在控制器在博弈时超过可获取的资源数量限制Mi=25。 图2 不同算法下控制器数量与控制器最大执行策略数关系 本文研究了网络安全中攻防冲突双方信息获取不完整以及资源受限条件下的动态博弈问题,并提出了一种改进的寻找马尔科夫完美均衡算法。案例结果为不完全信息、资源受限条件下博弈双方策略选取提供了一定借鉴。但是,目前的研究工作仅考虑了资源受限情况,未考虑观测过程中干扰、时延等带来的误差问题,故要真正在实践中体现其价值,还需要进行后续研究。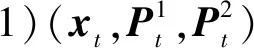
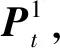

3 案例与分析


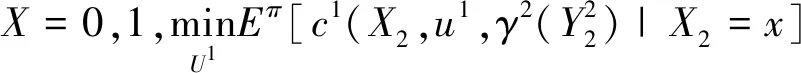

4 结束语

