基于RBF神经网络的复合材料固化均匀性优化
乔 巍,姚卫星,2,黄 杰
(1.南京航空航天大学飞行器先进设计技术国防重点学科实验室,江苏 南京 210016)(2.南京航空航天大学机械结构力学及控制国家重点实验室,江苏 南京 210016)
先进树脂基复合材料是航空航天、船舶及风电行业实现轻量化设计的关键性材料[1-2]。固化过程中树脂的交联聚合反应产生了大量热量,由于复合材料导热系数非常小,当结构厚度较大时,结构内部的温度场和固化度场呈现出较大的非均匀性,并产生了残余应力。这些残余应力使材料形成了初始损伤,从而降低了材料的力学性能。因此,研究降低温度场和固化度场非均匀性的优化方法,对于提高材料性能和产品固化质量具有重要意义。
固化过程中复合材料结构内部温度场和固化度场的非均匀性是产生残余应力和固化变形的主要因素之一。Shin等[3]建立了复合材料厚板的一维固化压实数值模型,模拟出树脂渗漏导致温度分布的不均匀。Yi等[4]用非线性有限元法分析了降温过程中复合材料内产生的残余应力,发现温度场对层间应力和平面应力都有明显影响。Ruiz等[5]采用有限差分法模拟结构固化过程中温度场和固化度场的变化,基于经典的层合板理论计算残余应力,在此基础上了研究了不同厚度结构的最佳工艺温度周期。
通过合理优化复合材料的工艺温度周期,可有效降低固化过程中温度场和固化度场的非均匀性。构建工艺温度周期的主要参数与温度场和固化场非均匀性之间的非线性映射关系,是优化设计的关键。代理模型是一种能很好解决非线性映射问题的方法,广泛应用于类似的优化问题[6-7]。Jahromi等[6]基于双隐含层的动态神经网络,开发出一种多段式工艺温度周期的优化方法,通过优化线段两端的温度,使温度场和固化度场的梯度最小,结果表明该方法具有较高的优化效率。Shah等[7]基于响应面模型和遗传算法,以残余应力最小为目标,提出不对称正交层合板工艺温度周期的优化方法,优化后残余应力降低了47%。
王晓霞等[8]基于Morris方法,定量分析了固化成型过程中结构厚度、热传导系数、固化温度、对流换热系数等4个关键参数对固化均匀性的影响程度。贺继林等[9]对复合材料固化理论模型进行因次分析,提取出无因次变量方程组,研究发现无因次式特征时间和树脂固化反应特征时间的比值与固化度差值间存在线性函数关系。
目前国内对于树脂基复合材料固化均匀性的研究以等温固化为主,对于应用更广泛的热压罐、树脂传递模塑(RTM)变温固化成型的研究相对较少。本文提出一种复合材料固化均匀性的优化方法,首先采用拉丁超立方试验设计方法和参数化的固化反应有限元模型建立固化反应的RBF神经网络,然后利用主要目标法和多岛遗传算法优化该网络以获取最优解,最后通过算例验证所提优化方法的有效性。
1 固化反应的数值模拟
1.1 理论模型
固化过程中复合材料结构内部热量来源于两部分,一部分由热压罐提供,通过金属模具和真空袋传递给复合材料结构,另一部分是复合材料自身化学反应释放的热量。考虑热-化学反应的强耦合作用,根据Fourier热传导定律和能量平衡原理,各向异性复合材料的三维热传导方程表示为[10]:
(1)
(2)
式中:t为时间;T为温度;α为固化度;kx,ky,kz为复合材料各向异性的热传导系数;Q为内部热源项;Hr为单位质量树脂化学反应释放的热量;ρp,cp分别为复合材料的密度和比热容;ρr,Vr分别为树脂的密度和体积含量;x,y和z分别代表沿着纤维、垂直纤维及厚度方向。
固化动力学方程反映了树脂固化率、固化度及温度之间的量化关系,通常采用宏观水平的唯象模型来描述。3501-6树脂的固化动力学方程为[10]:
(3)
其中Ki(i=1,2,3)为固化率系数,定义为:
(4)
式中:Ai为频率因子;ΔEi为活化能;普适气体常数R=8.314 34。
复合材料结构固化时外表面的边界条件为[10]:
(5)
式中:Ta为工艺温度;nx,ny和nz为边界外法线方向的余弦;h为边界的对流换热系数。对式(1)进行有限元离散,总体合成矩阵的求解方程为[10]:
(6)
式中:C,K,P及T分别为比热容矩阵、热传导矩阵、温度载荷向量及温度向量。采用向后差分法,由Gaierkin格式离散得:
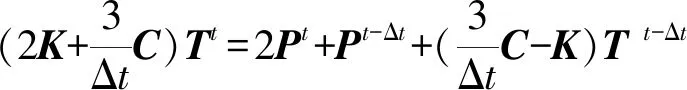
(7)
式中:Δt为时间增量。求解式(7)可得各个时刻节点的瞬时温度,代入式(3)求得瞬时固化度增量,节点的瞬时固化度更新为:
αt=αt-Δt+Δαt
(8)
式中:Δα为固化度增量。
1.2 有限元分析模型及验证
以文献[11]中AS4/3501-6环氧基复合材料为算例,验证有限元分析模型的合理性。结构几何尺寸为10.16 cm×10.16 cm×2.54 cm,铺层为[0/90] s,采用钢制模具在复合材料结构上下表面加热。模拟用材料性能与文献[11]一致,工艺温度周期为:先升温至116 ℃,保温1 h后升温至177 ℃,再保温2 h,最后降至室温,升温和降温的速度均为2.5 ℃/min。
采用ABAQUS软件建立了复合材料固化反应的三维有限元分析模型(FEM)。由于该软件不能直接分析带内热源的热传导问题,因此需将式(2)~式(4)及式(8)用Fortran语言写入用户子程序UMATHT。根据对称性,仅建立真实结构的四分之一模型,用三维热传递单元DC3D8划分网格。由于金属模具的导热系数非常大,可将工艺温度直接施加在结构的上下表面。
图1给出了固化过程中结构中心温度和固化度的变化曲线,图中温度和固化度的模拟结果与文献[11]的计算结果吻合良好,说明本文所建有限元分析模型具有较高的预测精度。
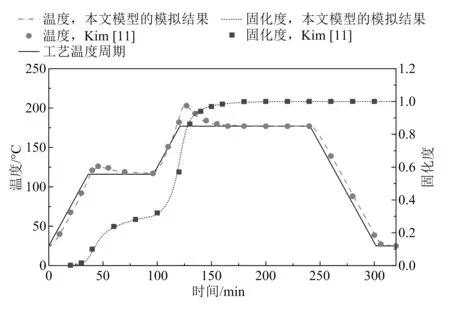
图1 固化过程中结构中心温度和固化度的变化曲线
2 固化均匀性的优化方法
将固化过程中某时刻复合材料结构内部温度场和固化度场的最大值与最小值的差值称为该时刻温度场和固化度场的梯度。固化过程中梯度越小,表明固化均匀性越好,反之则表明固化均匀性越差。
2.1 分区
将t时刻结构内温度梯度和固化度梯度分别记为Δα(t)和ΔT(t),进行有限元分析时,每个时间步对应2个梯度值。由于梯度值的数量过多,因此不能将它们直接作为神经网络的响应。本文采用分区法,将固化过程的时间历程分成若干时间区间,取出每个区间内梯度的最大值作为响应。
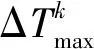

图2 时间历程的分区
(9)
那么,整个固化过程中最大温度梯度ΔTmax和最大固化度梯度Δαmax可表示为:
(10)
2.2 RBF神经网络
人工神经网络具有大规模并行处理、自适应性和高容错性等优点,选择合适的网络能逼近任何形式的非线性函数。Jin等[12]对4种典型代理模型进行了对比分析,结果表明RBF神经网络是最可靠的。
2.3 主要目标法
本文涉及到总的固化时间最短、温度梯度最小及固化度梯度最小的多目标优化问题。这三类目标的类型差别较大,很难根据理论或经验给出较合理的加权值。
本文选择主要目标法求解该多目标优化问题。主要目标法是一种化多为少的方法,从多个子目标函数中选出设计者认为最重要的一个目标,将其作为主要目标函数,而将其余子目标限制在一定的范围内,转化为新的约束条件,从而将多目标优化问题转化为单目标优化问题。
采用主要目标法,以总固化时间最短为目标,要求不同区间内最大温度梯度、最大固化度梯度均小于最大许用值。最大许用值由工程人员根据工程经验或设计要求给出。其他的约束条件还包括固化结束后复合材料的固化度大小于0.995,以保证材料具有足够的横向模量和强度[6]。因此,复合材料固化均匀性优化的数学模型可描述为:
findXi
min SumTime
αend≥0.995
XL≤Xi≤XU
式中:Xi为设计变量;i为设计变量的个数;k为时间区间的个数;XL和XU分别表示设计变量的上、下限;SumTime为总的固化时间;ΔT*,Δα*分别为温度梯度和固化度梯度的最大许用值;αend为固化结束时结构内部固化度的最小值。
对于上述优化问题,本文选择多岛遗传算法作为优化算法。多岛遗传算法是在传统遗传算法的基础上增加了岛的概念,将每个种群的个体分到几个岛上,通过不同岛上个体的不定期交换,增加了选择的多样性,具有全局寻优、抑制早熟现象等优势。
2.4 优化策略及步骤
复合材料固化均匀性优化策略的总体思想及步骤如下:
1)以升温速度、保温温度和保温时间为设计变量,采用拉丁超立方试验设计方法,从设计变量的取值空间中选取合适的样本点集。
2)采用Python语言和参数化结构建模方法,建立基于ABAQUS软件的固化反应的参数化有限元分析模型,并将选取的样本点集逐个代入有限元模型进行分析,从计算结果中取出不同时间区间的最大温度梯度、最大固化度梯度、总的固化时间及固化后结构内固化度的最小值,将它们作为响应。
3)将样本点集和获取的响应组成训练样本,对RBF神经网络进行训练,并测试网络的拟合效果,若不满足拟合精度要求,则返回步骤1),通过增加样本点数量,重新训练网络。
4)采用多目标法,以总的固化时间最短为目标,将其他子目标转化成约束,利用多岛遗传算法对训练好的网络进行优化,获得满足约束条件的最优解。
5)将最优解代入有限元分析模型进行检验,若响应的计算结果不满足精度要求,则将最优解和有限元计算结果返回步骤3),重新训练网络;若满足精度要求,优化结束。优化流程如图3所示。
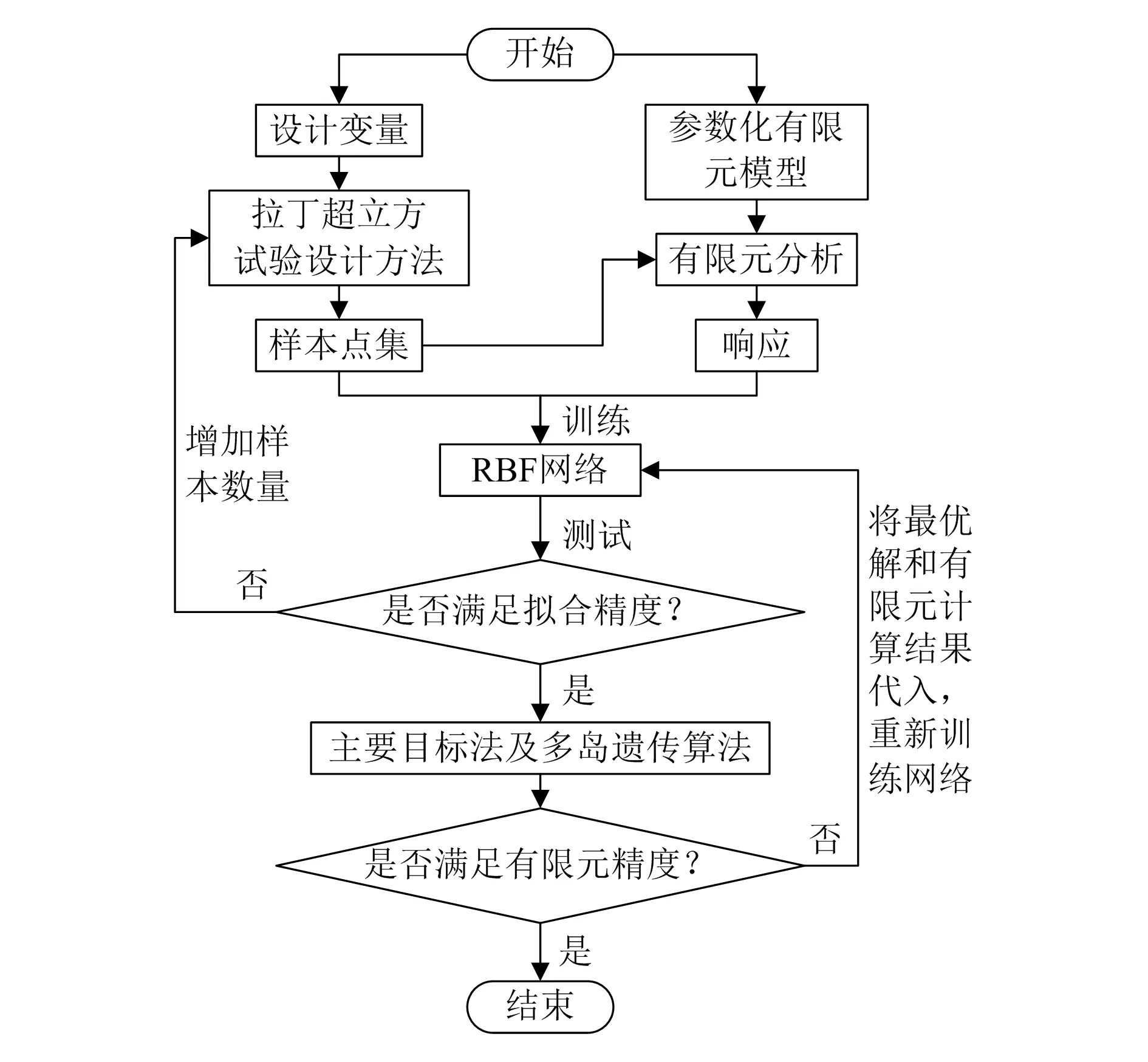
图3 复合材料固化均匀性优化的流程图
3 优化设计
对文献[11]中AS4/3501-6环氧基复合材料固化反应的工艺温度周期进行优化。以2个升温速度、2个保温时间及1个保温温度为设计变量,如图4所示。第二保温段的温度与树脂基体的玻璃化转变温度相关,该温度会影响到固化后复合材料的力学性能。降温前复合材料已完成固化,因此降温速度对固化均匀性没有影响。本文在优化分析中保持第二个保温段的温度和降温段的降温速度不变。设计变量的详细参数见表1。
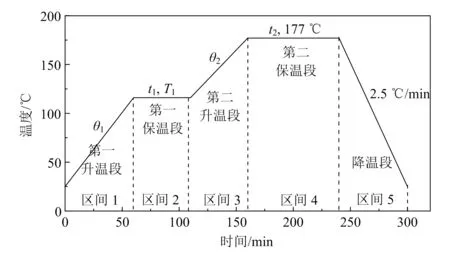
图4 固化过程时间历程的分区

表1 设计变量
3.1 网络的拟合效果
利用拉丁超立方试验设计方法,从表1中5个设计变量的取值范围内生成60组样本点集,代入有限元分析模型进行计算以获取响应,将样本点集与响应组成60组样本。随机取出50组样本对RBF神经网络进行训练,剩余10组样本用于测试网络。用可决系数R2来表征网络的拟合效果,R2值越趋近于1,表示网络的拟合效果越好。
图5给出了RBF神经网络的拟合效果。从图中计算结果可知,10组响应的可决系数R2均大于0.9,说明所建网络具有较高的拟合精度。
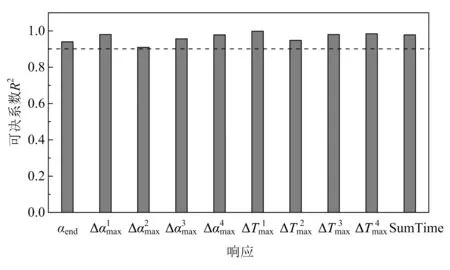
图5 RBF神经网络的拟合效果
3.2 结果与分析
初步研究发现,ΔT*和Δα*的取值对优化结果的影响较大。为了研究的方便,给出3组优化方案,并对它们的优化结果进行对比分析。选取的优化方案如下:方案A,ΔT*=5 ℃,Δα*=0.05;方案B,ΔT*=6 ℃,Δα*=0.06;方案C,ΔT*=7 ℃,Δα*=0.07。
采用多岛遗传算法优化RBF神经网络,以获取不同优化方案下设计变量的最优解,优化结果见表2。将表2中设计变量的优化结果代入有限元分析模型进行计算,以检验RBF神经网络给出的响应的计算精度,有限元模型的计算结果见表3。对比表2和表3中响应的计算结果,结果显示它们的最大相对误差为8.54%,说明RBF神经网络给出的响应具有较高的拟合精度。
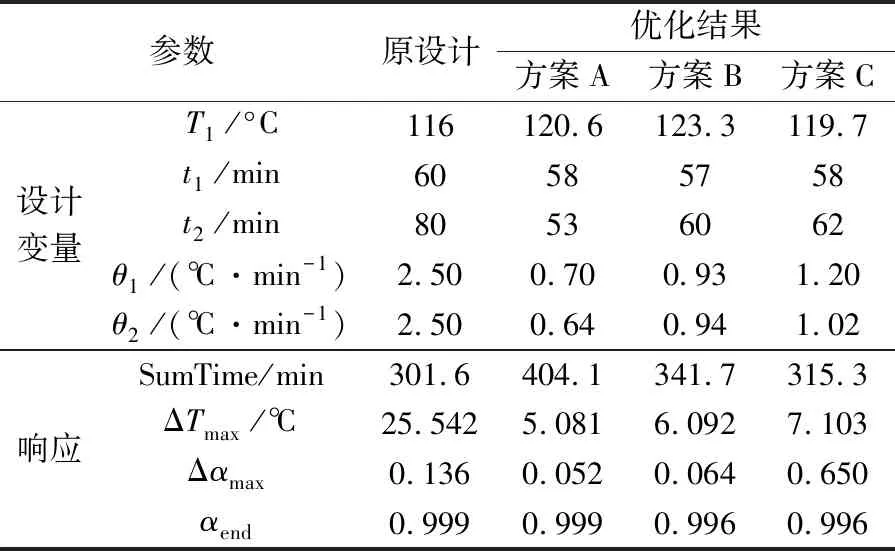
表2 优化结果与原设计的对比
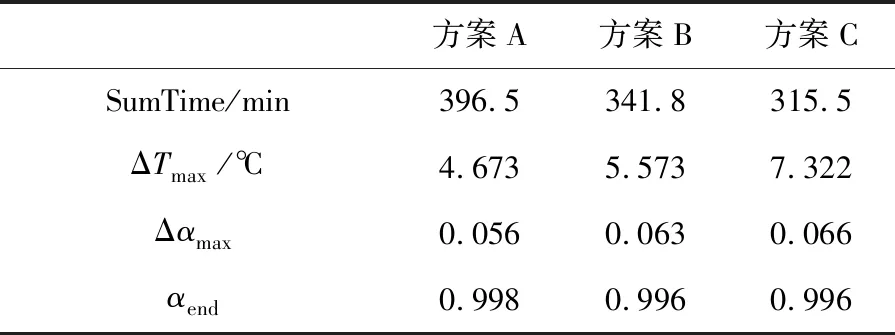
表3 有限元分析模型检验优化结果
表4给出了3种优化方案的优化效果,从降低制造成本的角度考虑,方案C较好。该方案总的固化时间最短,不仅降低了能耗,而且提高了工作效率。相比原设计,方案C在总的固化时间仅增加4.71%的情况下,将温度梯度和固化度梯度的最大值分别减少了71.34%和51.47%,有效提高了复合材料的固化均匀性,表明优化效果显著。
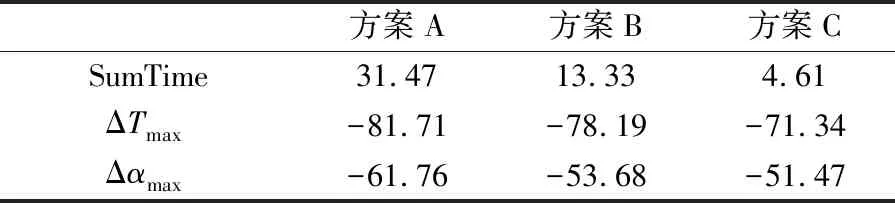
表4 优化效果
本文所提优化方法具有较强的适用性,基于商用ABAQUS有限元软件,可分析形状复杂结构的固化反应,并优化其工艺温度周期。但该方法没有考虑固化初期树脂的流动性,不适用于RTM液态成型固化反应的分析和优化。
4 结束语
本文提出一种基于RBF神经网络的复合材料固化均匀性优化方法。拉丁超立方试验设计方法选取设计变量的样本点,固化反应的参数化有限元模型计算响应,从而建立固化反应的RBF神经网络。通过主要目标法和多岛遗传算法优化神经网络。算例的计算结果显示,相对原设计,在总的固化时间仅增加4.71%的情况下,优化后温度梯度和固化度梯度的最大值分别减少了71.34% 和51.47%,表明本文所提优化方法简单易行、优化效果显著。

