基于多尺度卷积神经网络的短期电力负荷预测*

许言路， 武志锴， 朱赫炎， 王斌斌， 邓卓夫

(1. 国网辽宁省电力有限公司 经济技术研究院， 沈阳 110015； 2. 东北大学 软件学院， 沈阳 110819)

当前电力行业在开放售电环境下需要精确的短期负荷预测(STLF)，以实现电力负荷的规划和管理策略的实施.为了提高预测精度，在过去的几十年中已经提出了各种新的电力负荷预测技术.由于电力负荷及其影响因素的非线性和随机性，电力负荷预测已成为电力市场实体面临的最具挑战性的任务之一.用于电力负荷预测的模型大致可以分为：统计模型、基于知识的专家系统模型、混合模型及基于人工智能的模型.

传统统计模型[1](如自回归模型)研究了电力负荷及其影响因素之间的定性关系，并且易于实现.然而，这些统计模型在很大程度上依赖于当前负荷与历史负荷之间的相关性，在选择适当的非线性函数时面临很大困难并且计算成本高.

在所有可用的预测模型中，基于人工神经网络(ANN)的模型在解决STLF问题方面吸引力最大.文献[2]使用多层感知机(MLP)结合气候数据进行每日负荷预测；文献[3]对影响电力负荷的因素进行PCA及ICA分析，降低数据维度和BP神经网络的搜索空间；文献[4]广泛讨论了神经网络的应用，并深入分析了其短期负荷预测的性能.传统ANN算法需要搜索庞大的函数空间，且函数空间中有很多代价很大的局部极小值，这使得模型的求解速度和精度都受到影响.

循环神经网络(RNN)是可以适应连续时间步骤之间依赖性的一类算法，然而，普通RNN易产生梯度消失/爆炸的问题，这使得学习长期依赖性变得困难.具有长期短期记忆单元(LSTM)的循环神经网络作为梯度消失问题的解决方案，能够模拟时间序列数据中的短期和长期时间相关性，使其在序列处理方面表现出良好的效果[5]；文献[6]基于设备级电量数据，使用LSTM模型来预测建筑电力负荷；文献[7]展示了基于序列到序列的LSTM模型在预测短期电力负荷方面的性能；文献[8]提出了一种聚合LSTM和CNN的模型，用于小时级的电力负荷预测.LSTM的缺点是它的复杂性，2014年首次提出的门控循环单元(GRU)是最成功的LSTM变体之一，然而，即使经过优化，LSTM和GRU模型在面对很长的(如长度超过100)输入序列时，依然会丢失长期数据中的关键信息，从而限制了精度的提升.

最近的研究结果表明，具有卷积架构的神经网络在语音合成、语言建模及机器翻译等序列任务中表现良好，进而提出了一个课题：基于卷积的网络能否解决上述问题，并在具有时间序列特征的电力负荷预测方面也有更佳的表现?本文首先将电力负荷数据及相关影响因素建模为时间序列问题，随后提出一种多尺度信息融合卷积神经网络(MS-ConvNet)来预测6 h电力负荷.MS-ConvNet引入因果逻辑约束增强时间序列特征表达，利用多尺度卷积描述不同长度时域数据相互关系，并设计残差网络结构提升了网络深度和预测精度，实验结果表明，MS-ConvNet模型的精度优于MLP、LSTM和GRU等模型.

1 问题定义

电力负荷预测根据预测时间长短分为4类：1)非常短期的负荷预测，用于预测1 h内的负荷需求；2)短期负荷预测，预测一天至一周的负荷需求；3)中期负荷预测，预测一周至几个月的负荷需求；4)长期负荷预测，预测的时间段在几个月至几年之间[9].其中，STLF为电力系统的控制和调度提供精确的负载需求，同时要求较高的实时性.本文关注于STLF，目标是通过对电力负荷数据及相关影响因素进行时间序列建模，再通过提出的网络模型预测未来6 h的电力负荷.

假设xt是包含时刻t数据的一个向量(包含电量负荷、最高温度、最低温度及节假日等)，用一个输入序列(x0，x1，…，xT)来预测相应的输出(y0，y1，…，yT).

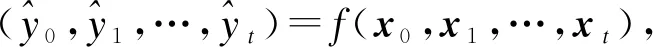
(1)

代入后得到的待优化代价函数为

(2)

2 多尺度信息融合卷积神经网络

2.1 具有因果关系的卷积

如问题定义中所述，模型基于两个原则：一是网络的输入与输出长度相等；二是网络中任意时刻t对应的节点只接受t时刻之前的信息.针对第一点，本文使用了一个一维的全卷积网络(FCN)；为了实现第二点，使用了具有因果关系的卷积保证任何时刻网络中某一节点都只获取了过去时刻的信息.这个设计的主要缺点是：为了实现对较长历史规模的有效性，需要一个非常深的网络或者非常大的过滤器，而这两种方法都需要占用大量的计算资源，因此，提出了多尺度信息融合优化技术，使得模型可以在较小的过滤器下覆盖更大的范围.

2.2 多尺度信息融合卷积

一个简单的因果卷积只能回顾线性尺度的网络宽度，因此本文使用了多尺度信息融合的因果卷积，可以融合指数级大小的接受域.普通一维卷积的定义为：设F∶Z→R是一个离散函数，若Ωr=[0，r]∩Z，且k∶Ωr→R是一个尺寸大小为r的过滤器，则卷积操作可以被定义为

(3)

设l是一个尺度因子，则多尺度信息融合的一维卷积操作被定义为

(4)

式中：s为卷积的起始位置；p为过滤器中位置值，lp为向前跨越的尺度.因此，尺度卷积相当于在过滤器相邻的点之间引入了固定的间隔，当l=1时，多尺度的卷积就变成了一个常规的卷积，使用更大的尺度因子可以使上层节点融合更大范围的输入，能够有效地提取更大范围的信息.

本文提出了两种方式来扩大接受域：选择更大的过滤器尺寸r或者增大尺度因子l，其中一层的有效范围是(r-1)l+1.增加深度也会给尺度的大小带来指数级的增长，这确保了在有效的输入长度中，模型总是能够提取每一个输入的信息.图1为带有因果卷积的多尺度信息融合示意图.

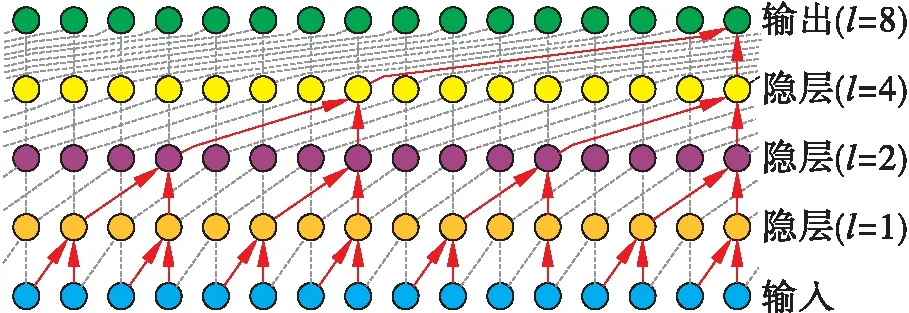
图1 多尺度信息融合示意图Fig.1 Schematic diagram of multi-scale information fusion

2.3 残差学习

残差网络(ResNet)的提出使神经网络模型开始向深度发展.在传统神经网络结构中，如果单纯地增加网络的深度会引起梯度消失、爆炸或准确率退化的问题.

对于梯度消失、爆炸问题，ResNet通过标准化得以解决；对于准确率问题，ResNet通过残差学习来解决.残差块是包含一系列变换Z的一个分支，残差连接是将残差块的输出和一个恒等映射的输出相加并激活，即

Y=Z(X，Wi)+X

(5)

式中：Z(X，Wi)为需要学习的残差映射；Wi为过滤器参数.残差连接允许层有效地学习对恒等映射的修改，而不是学习整个变换，这已经被证明对于深度网络非常有用.

ResNet最初被设计用来解决图像识别问题，但是其中采用的残差学习和标准化的思想可以被应用到任意的模型中用来解决相似的问题.

2.4 MS-ConvNet

MS-ConvNet中的一个残差块如图2所示.在一个残差块里，包含多尺度信息融合、标准化和激活函数，激活函数采用整流线性单元(ReLU)，此外，为了防止过拟合及增加模型抗噪能力，在模型最后加入了一层Dropout[10].

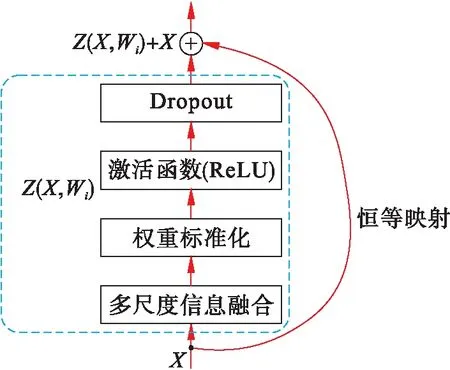
图2 MS-ConvNet模型中的残差块Fig.2 Residual block in MS-ConvNet model

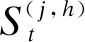
(6)

在MS-ConvNet模型中，对卷积输出使用了参数标准化，参数标准化是对过滤器参数W进行标准化，是通过一个标量g和一个矩阵V对参数矩阵W进行尺度变换，其变换公式为

(7)

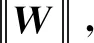
(8)

(9)

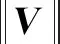
总的来说，权重标准化解耦了参数矩阵的范数和方向，加速了收敛，保证了梯度的稳定，不会爆炸或者消失；同时又解决了批标准化的数据依赖性，计算开销也降低了许多；相比于批标准化，该方法无法将每一层特征尺度固定住，因此本文设计了一种初始化方法，在初始化时利用了最小批的信息，保证了输入特征在初始化时均值为0，方差为1.

3 实验与结果

本文使用某地电网2014～2018年负荷数据对模型进行评估，同时也从互联网搜集了此地区每日最高气温、每日最低气温以及节假日数据.图3显示了一天24 h电力负荷分布的箱形图，从图3中可以看出，每个小时的数据服从单独分布，有不同的均值和方差.在神经网络中，这种输入数据的不均匀分布会造成梯度信息的爆炸或消失.为了解决该问题，本文对数据进行标准化预处理，同时在模型中使用权重标准化提升模型的鲁棒性.

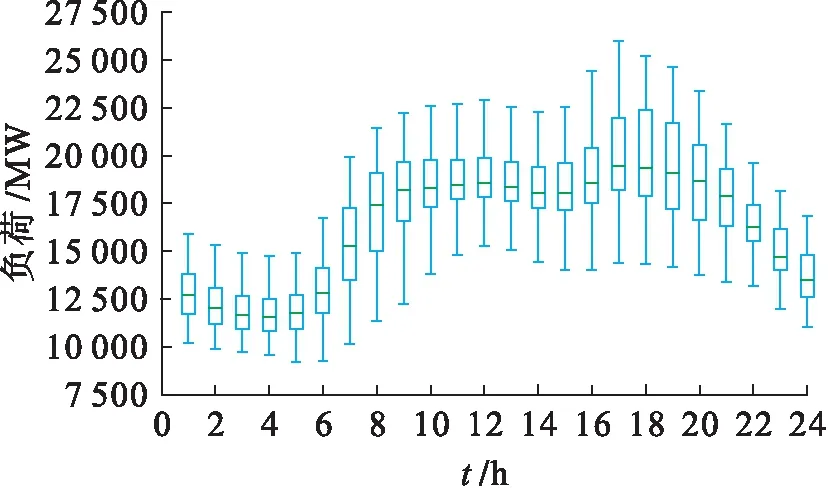
图3 一天24 h电力负荷分布箱形图Fig.3 Box diagram of electric load distribution in 24 h

首先对数据进行最大绝对值归一化，即所有数据除以数据集中的最大值，一共得到了31 128条数据，其中前80%作为训练集，后20%作为测试集.众所周知，更宽和更深的网络可以为深度模型带来更加精确的结果，受实验条件所限，模型基于相似的参数总量来选取参数，最终选择最优表现的参数进行分析.使用10天总计240 h的数据作为输入序列.模型使用了如2.4节中描述的残差块，每个残差块中包含4层卷积层，与其对应的尺度因子l设置为[1，2，4，8]，共堆叠了8层残差块，批次大小为128.每层中过滤器的数量为32，过滤器大小为8.训练采用TensorFlow后端的Keras框架，使用学习率衰减和Adam优化，硬件则采用了两块英伟达P4计算卡的云服务器.

本文对比了MLP，LSTM，GRU和MS-ConvNet几种神经网络的测试结果，测试中都使用相同的240输入步长以及相同的Adam优化器，LSTM和GRU都采用了效果最好的三层结构.性能对比评估采用三种指标：平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和判定系数(R2).

训练过程中测试集MAPE曲线如图4所示，可以看出这4种模型经过Adam优化后，都可以在较短训练步数内迅速收敛.但是需要注意的是，GRU和LSTM由于RNN模型的特殊性(每个单元的训练都需要等待上一个单元的输出)，单步训练消耗的时间是MS-ConvNet的数倍，因此MS-ConvNet实际收敛耗时远低于GRU和LSTM.

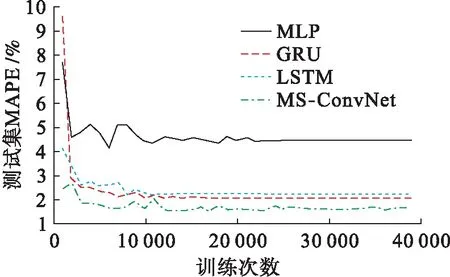
图4 模型训练过程中测试集MAPE曲线Fig.4 MAPE curves of test set during model training

图5显示了4种模型对应测试集结果的散点图.每个点代表一个测试样本，中间是一条Y=X的斜线.点距离中间线的距离越近，结果越准确.从图5中可以看出，MLP子图中点分布偏下，说明MLP更倾向于预测更低的结果，这会造成频繁的计划供电量不足；相较于前三个子图，MS-ConvNet子图中的点更紧密地聚集在斜线周围，这说明MS-ConvNet在较大的比例测试样本上做出了更准确的判断.

通过多次实验得出的测试结果对比如表1所示.以过去多年国内外广泛采用的模型作为测试基准，可以看出在多种评估手段下，各种神经网络都表现出了一定的预测能力.LSTM和GRU的表现优于MLP，MS-ConvNet取得了这次实验中最优结果，相较于MLP模型，MAPE降低了63%，MAE降低了65%，而R2从0.884提升到0.976.相对于LSTM和GRU，MS-ConvNet的结果也显示了明显的进步，说明模型中各种设计的结构能够很好地适应负荷序列数据.

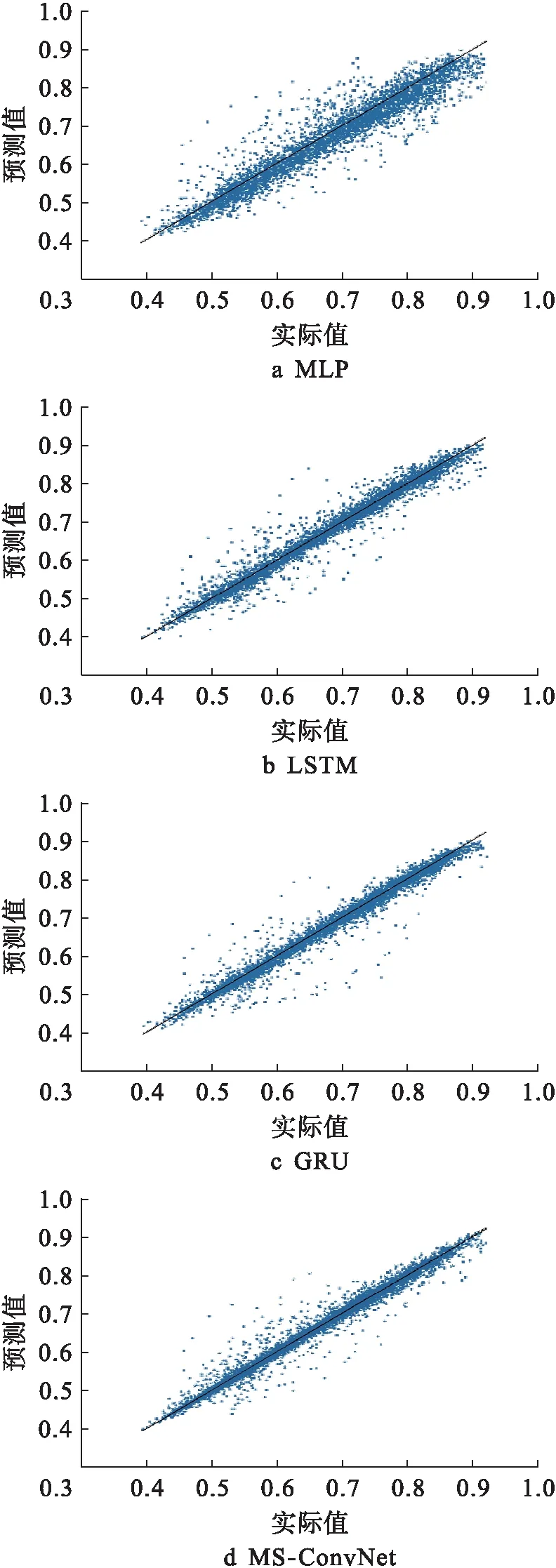
图5 四种模型测试结果散点图Fig.5 Scatter diagrams of test results with four models

负荷数据常常由于采集设备故障和通信异常而造成数据缺失或数据异常，健壮性较差的模型容易因此产生不可靠的预测.为了测试MS-ConvNet的鲁棒性，在一定比例的归一化负荷数据上随机加入了标准差为0.2的白噪声，加入噪声数据的比例分别为5%、10%、20%，然后进行训练和测试，测试结果如表2所示.

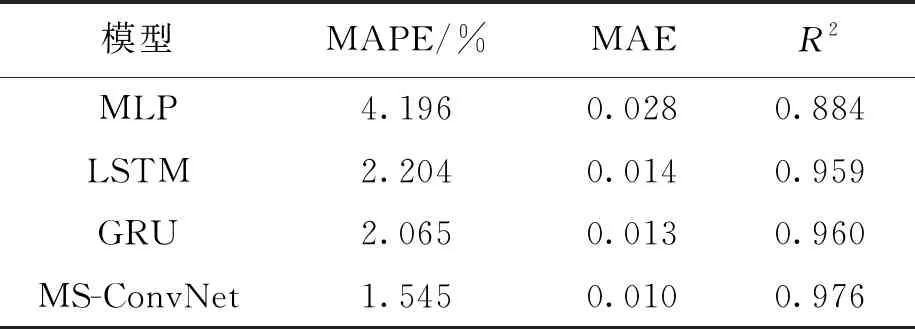
表1 测试结果性能对比Tab.1 Performance comparison of test results

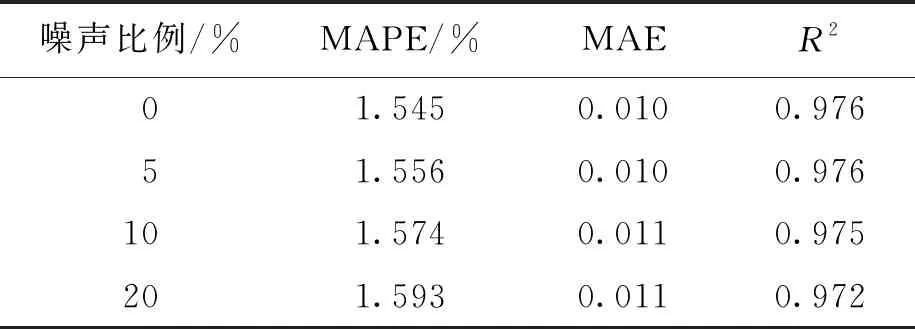
表2 加入白噪声的鲁棒性测试Tab.2 Robustness test with white noise addition

从表2中可以看出，添加一定量的白噪声对测量结果影响很小，这说明提出的模型在面对噪声时具有优良的鲁棒性.同时本文对比了几种模型的训练和预测时间，结果如表3所示.

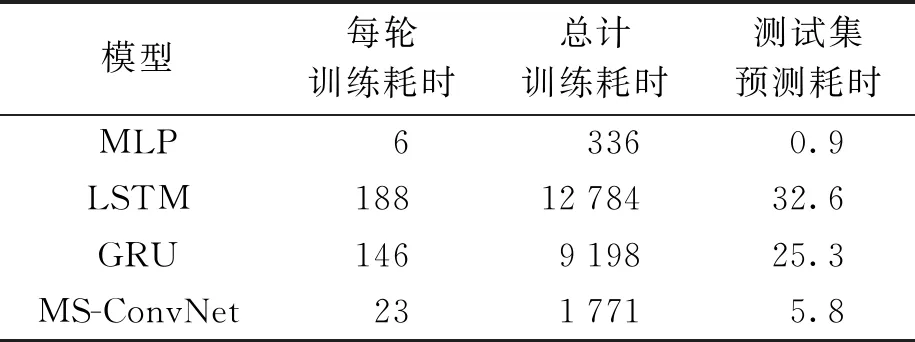
表3 模型效率对比Tab.3 Model efficiency comparison s

得益于基于GPU的大规模并行运算技术的成熟，神经网络繁重计算可以在较短的时间内完成.从表3中可以看出，MLP由于其简单的结构和较少的参数量，因此拥有最少的训练和测试耗时.LSTM和GRU因为其循环运算的结构，每一步预算必须基于上一步的输出，所有耗时较大.其中GRU由于简化了内部结构，因此一定程度降低了运算量.MS-ConvNet的整体网络可以并行运算，因此耗时较LSTM和GRU大幅降低，其中对测试集的6 168条数据进行测试仅耗时5.8 s，说明MS-ConvNet在工业级别的大数据并行预测方面具有良好前景.

4 结 论

本文通过实验证明了MS-ConvNet在短期电力负荷预测方面具有良好的精确度、鲁棒性和运行效率.MS-ConvNet相较于LSTM和GRU表现出良好的并行能力，这一点在短期电力负荷预测时对实时性要求较高的情况下尤其重要.过去十几年，神经网络在图像分类、序列处理等许多方面都展示出了优秀的性能和健壮性.在电力负荷预测方向，基于神经网络的模型也得到了更多的应用，相信随着研究的深入，基于卷积的神经网络模型也可以推动电力负荷预测的进一步发展.