大跨铁路梁桥最大悬臂阶段的静风安全性分析
杜立凡 王卫锋 郑恒斌

摘 要:在桥梁挂篮悬臂浇筑施工过程中,风荷载与桥梁结构的相互作用是一项工程风险因素。为评估桥梁挂篮悬浇施工过程中结构的抗风安全性,同时为桥梁抗风设计提供有效依据,以某大跨铁路连续梁橋为背景,基于CFD数值模拟结合规范建议公式确定了桥梁关键截面的三分力系数,而后采用Midas Civil建立了考虑桥梁施工全过程的有限元模型。针对主梁最大悬臂阶段将均匀对称、非均匀对称和龙卷风荷载分别与对称及非对称施工荷载工况组合,将结构预存状态与静风荷载效应叠加,以此全面分析主梁最不利施工阶段的静风安全性。结果表明:静风荷载引起主梁横向位移最大值可达到6.98 mm,竖向位移最大值可达到5.03 mm,龙卷风工况对结构位移最为不利;各关键位置应力最大值,最小值均出现在对称均匀加载工况,对称均匀加载工况对结构应力最为不利。为确保结构安全建议在桥梁挂篮悬臂浇筑施工过程中,考虑风荷载效应的影响。
关键词:桥梁工程;悬臂施工;静风荷载;CFD方法;三分力系数;安全性
中图分类号:U441.2
文献标识码: A
桥梁结构的施工工程复杂庞大,工程建设过程中面临来自自然界气候条件、材料性能等不确定性因素影响,一旦发生事故,将会造成非常巨大的生命及财产损失。风荷载引起的桥梁破坏发生面较广,桥梁结构在风荷载作用下可能发生失稳甚至破坏[1-3]。在施工阶段下,桥梁结构对风荷载的作用更为敏感,结构过大的风响应会对施工及结构安全造成不利影响[4-5]。而最大悬臂阶段是桥梁挂篮悬臂施工过程中最不利的阶段,结构在此阶段受风荷载的影响最大[6-8]。所以,对桥梁的最大悬臂施工阶段进行风安全评估是有必要的。由于在大跨梁桥悬臂浇筑的过程中,T构两侧悬臂难以做到完全对称,不平衡荷载是悬臂阶段风安全问题中一个需要考虑的因素[9]。施工过程中结构状态有一个叠加的过程,静风荷载作用在叠加下可能导致结构产生更大的位移和内力,所以施工过程的结构状态与静风荷载效应的叠加也是需要考虑的问题。
风洞试验是目前风荷载研究中最可靠的方法,但风洞试验存在费用高,时间长,试验环境不安全等问题。计算流体力学(computational fluid dynamics,CFD)数值模拟方法不受实验模型与设备的限制,可以在一定程度下替代风洞试验取得关键断面的气动参数。本文以某铁路大跨连续梁桥为背景,基于CFD方法对主梁关键断面的三分力系数进行了求解,参考《公路桥梁抗风设计规范》综合考虑确定了桥梁计算风参数,在此基础上将风荷载分别作用于对称与非对称施工荷载的结构模型中,分析结构应力及位移状态以期全面评估该桥最大双悬臂阶段的静风安全性问题。
1 工程概况
深茂铁路某特大桥为连续梁结构,采取挂篮悬臂浇注施工。该桥位台风频繁,最大风力高达14级,风向、风速随季节变化不定。其中最大主跨为100 m的连续梁,相对于其他小跨径的连续梁,在最大双悬臂施工阶段中受风荷载的影响最为不利,有针对性的选取该桥进行风荷载作用下挂篮悬臂施工安全分析研究。
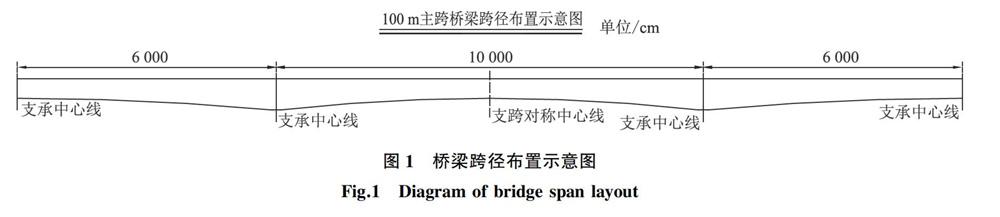
主跨为100 m的预应力混凝土连续梁桥,其跨径布置为(60+100+60)m。桥梁上部结构梁体采用变截面单箱单室结构。箱梁顶宽12.6 m,直腹板。各控制截面处梁高分别为:端支座处和跨中处为4.50 m,中支点处梁高7.20 m,梁高按圆曲线变化。箱梁采用C60高性能混凝土。箱梁采用三向预应力体系,钢绞线标准强度1 860 MPa、公称直径15.2 mm。桥梁跨径布置图1所示。
2 基本风参数的确定
根据全国基本风速值和基本风速分布图中的取值,桥址地区重现期为10年、50年和100年的基本风速分别为27.1 m/s,33.8 m/s和35.0 m/s。地表粗糙度系数α取值为0.16,地表类别属于B类场地。由此,偏安全的取桥址处按重现期为100年的设计基本风速为U=35.0 m/s[10]。
根据设计资料以及《公路桥梁抗风设计规范》(JTG/T D60-01—2004)[11],简称“抗风规范”,可计算得到100年重现期的主梁、主墩处设计基准风速,重现期为10年的施工期主梁、主墩设计基准风速,以及最大悬臂阶段主梁、主墩静阵风风速。计算结果如表1所示。
3 主梁静力气动力系数数值模拟
3.1 CFD数值模拟过程
当主梁处在平均速度为U的均匀流场中时,单位梁长的主梁会受到静风荷载包括阻力、升力和升力矩三个分量[12]。对于三个分量的描述通常可采用体轴坐标系和风轴坐标系表示如图2所示,其中FD、FL和FV、FH分别为风轴坐标系下和体轴坐标系下单位梁长所受的静风阻力和升力。
数值风洞模拟主梁断面的气动阻力系数、升力系数和升力矩系数三个分量。以风轴坐标为参考坐标轴,以断面的形心为参考点。针对目标桥梁关键断面的三分力系数的数值模拟,采用目前CFD领域应用较广泛的大型计算流体软件ANSYS FLUENT 14.5进行,首先在ANSYS ICEM CFD 14.5中进行前处理工作完成几何模型的建立和网格的划分,随后将几何模型导入到ANSYS FLUENT 14.5中。计算中,正确设定了求解边界条件和符合实际桥梁工程的湍流模型[13]。风攻角变化范围为-3~3°,分别求得对应不同风攻角的三分力系数[14-15]。
3.2 三分力系数模拟结果
计算得到的体轴坐标系下主梁跨中、L/4和墩顶截面共3个断面不同风攻角下的三分力系数。三分力系数随风攻角变化趋势见图3—图5所示。
由图3—图5的计算结果可知:截面的三分力系数受到截面高度及风攻角的影响。其中阻力系数受截面高度影响最为显著,截面高度越大对应的阻力系数亦越大。升力系数受风攻角影响较大,由于箱梁上下表面压力差随风攻角发生变化,导致不同风攻角下的升力系数差异明显。三种断面的升力距系数间于0.135 8~0.208 6,升力矩系数整体变化较小。墩顶截面的阻力系数随风攻角变化幅度与L/4截面及跨中截面相比较大,跨中截面的升力系数及升力矩系数随风攻角变化幅度较大。
3.3 阻力系数的选取
由于“抗风规范”中提供了阻力系数的计算方法,在此将由CFD数值模拟得到的阻力系数与“抗风规范”计算得到的阻力系数进行对比,选择阻力系数的合理取值。
“抗风规范”条文4.3.2中,对于“工”“Ⅱ”以及箱型截面的主梁的阻力系数CH可按下式计算:
根据式(1)可对桥梁各截面主梁的阻力系数CH进行计算,主梁不同梁高下的阻力系数计算结果见图6所示。从图中可看出,“抗风规范”中主梁的阻力系数CH取值范围为1.826~1.927,这比前述采用CFD方法计算得到的0°风攻角下的截面阻力系数增大较显著,表明“抗风规范”得到的阻力系数值更为保守。由此本文在进行桥梁静风安全性分析时,采用偏保守的“抗风规范”得到的阻力系数值。
4 桥梁三维仿真有限元模型建立
根据深茂铁路目标桥梁的结构及施工特点、最大双悬臂阶段抗风分析的具体要求,采用有限元逐步正装计算法,利用桥梁有限元通用分析软件Midas Civil进行桥梁施工过程的模拟计算。
对于目标桥梁施工过程有限元模型建立时,考虑了以下因素:
(1)采用空间杆系结构模型,桥墩及主梁均模拟为空间梁单元,结构的离散主要按主梁施工梁段划分,在墩顶受力复杂处的适当加密。最大双悬臂阶段单墩支撑的主梁共有35个节点、34个梁单元。为简化分析的考虑忽略了下部结构中的承台和桩基础,将墩底固结。对于主梁施工过程中的临时锚固墩,采用约束主梁约束的方式模拟。
(2)挂篮荷载以临时竖向集中力荷载的形式设置。预应力荷载按照规范的要求考虑了孔道摩擦、锚具变形等引起的预应力损失。考虑了混凝土收缩徐变的影响
5 桥梁静风安全性分析
5.1 桥梁静风力计算
施工阶段的风荷载应采用阵风风荷载。横桥向风作用下主梁单位长度上的横向静风荷载可按下列公式计算:
对于连续梁桥而言,由于桥梁自身的刚度较大,可以忽略静风升力矩对主梁的作用,同时根据“抗风规范”,主墩仅考虑静风阻力作用。由此,在桥梁静风力计算中,最大悬臂阶段主梁考虑静风阻力和升力,主墩仅考虑静风阻力作用。
5.2 风荷载加载工况
对大跨预应力混凝土连续梁桥最大悬臂阶段进行抗风安全性分析时,为能够真实反映出风荷载对受力的影响,需要采用多种加载方式将静风力作用至桥梁上。考虑结构受力的不利情况,对目标桥梁最大悬臂阶段的静风荷载加载主要采用三种工况,计算桥梁关键断面如桥墩墩底截面及悬臂根部截面的混凝土应力值。具体如下:
加载工况1:在悬臂的两边主梁按相同风压加载,并考虑作用于桥墩上的横向风力。加载示意见图8(a)所示。
加载工况2:考虑风场的不均匀性,在悬臂的两边主梁分别按1∶0.5倍的不均匀风压加载。加载示意见图8(b)所示。
加载工况3:考虑龙卷风袭击,在悬臂的两边主梁都施加100%的风荷载,但是两端风荷载的方向相反,并只有半跨作用有风荷载。加载示意见图8(c)所示。
5.3 对称施工荷载下的静风安全分析
在大跨连续梁桥主梁悬浇施工过程中,忽略可能出现的悬臂两端浇筑不同步、混凝土容重存在偏差等不对称施工荷载的影响,近似认为悬浇过程中悬臂两端施工荷载对称。
5.3.1 对称施工荷载下位移结果分析
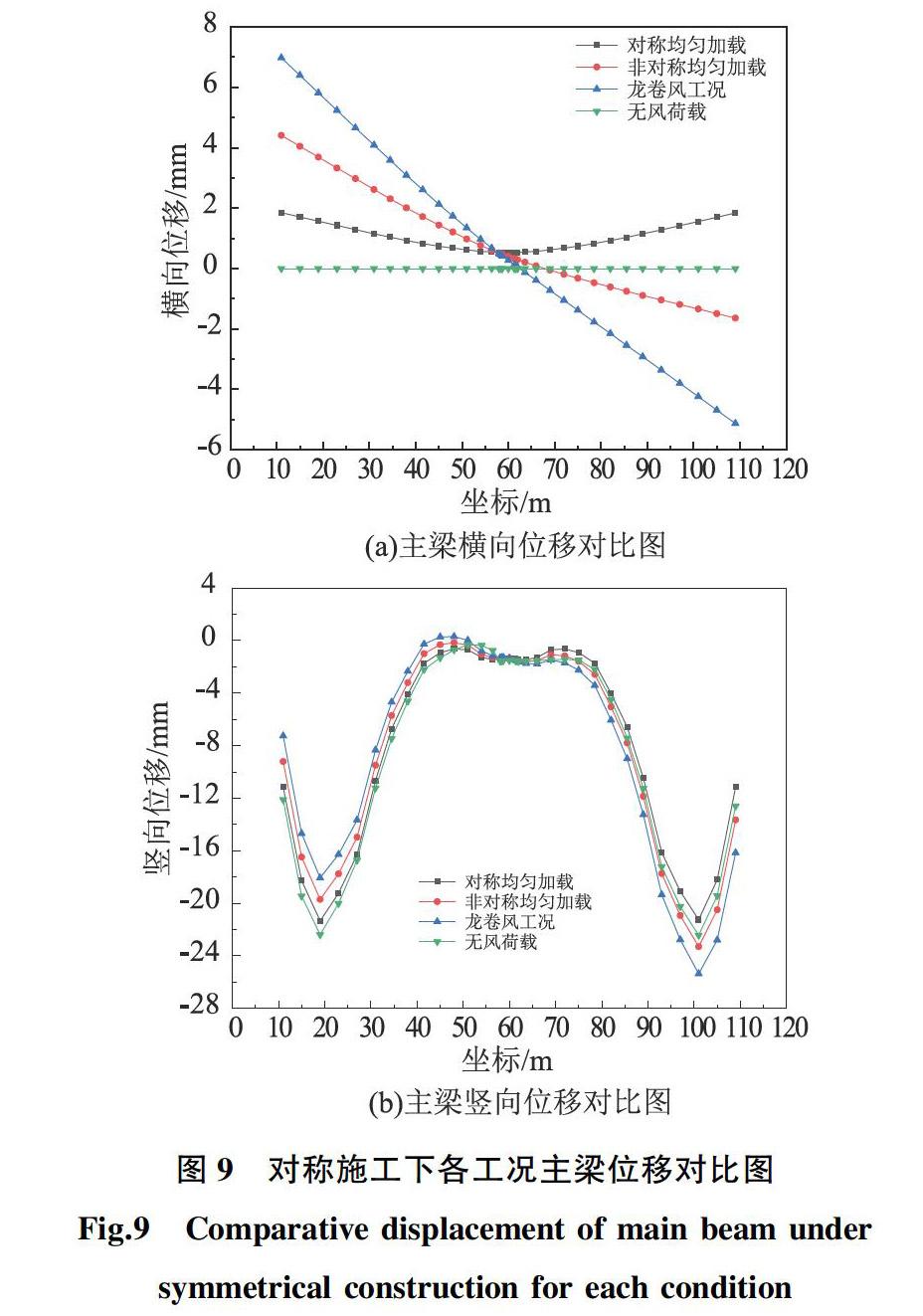
计算得到三种风荷载加载工况下主梁最大悬臂阶段各节点在整体坐标系下的位移值,不同风荷载加载工况下主梁横向位移、竖向位移对比图见图9所示。
由图9的计算结果可知:风荷载对主梁最大悬臂阶段的横向位移影响最为显著。对称风荷载下主梁两侧悬臂的位移方向一致,位移极值较小,非对称风荷载及龙卷风荷载下两侧悬臂位移方向相反,引起主梁发生横向旋转及竖向倾斜。龙卷风工况所引起的桥梁横向位移及竖向位移极值最大,其中主梁横向位移最大值为6.98 mm,竖向位移最大值为4.86 mm,表明龙卷风工况对结构位移最为不利。
5.3.2 对称施工荷载下应力结果分析
计算得到的桥梁最大双悬臂阶段不同风荷载加载工况下全桥各单元截面压应力最大值、最小值统计结果直方图见图10所示。其中1—12号单元分别对应箱梁左侧12#块—1#块, 13—22号单元对应箱梁0#块, 23—34号单元分别对应箱梁右侧1#块—2#块,35—39号单元分别对应主墩墩底至墩顶。
各关键位置在各风荷载加载工况中应力均为压应力,且满足规范限值要求。其中,主梁悬臂根部位置在各风荷载加载工况中压应力最大值为9.07 MPa,最小值为3.02 MPa;墩顶位置在各风荷载加载工况中压应力最大值为1.39 MPa,最小值为0.84 MPa;墩底位置在各风荷载加载工况中压应力最大值为2.02 MPa,最小值为1.10 MPa。
由图10的计算结果可知:主梁截面应力最大值出现在悬臂根部位置,往悬臂端部方向应力逐渐减小。风荷载主要影响主梁悬臂根部及桥墩部位的应力变化,对悬臂端部基本无影响。非对称风荷载及龙卷风荷载导致两侧悬臂根部附近應力出现明显的不对称。悬臂根部、墩顶、墩底三个关键位置的应力最大值,最小值均出现在对称均匀风荷载加载工况,表明对称均匀风荷载对结构应力最为不利。
5.4 非对称施工荷载下的静风安全性分析
在大跨梁桥悬臂浇筑的过程中,T构两侧悬臂施工荷载的非对称性是难以避免的,为考虑非对称施工荷载对结构的不利影响,在分析中考虑了下述荷载工况:
(1)T构两侧梁体自重不平衡,一侧梁体自重增大5%,而另一侧梁体自重不增大;
(2)挂篮、施工机具的偏差,一端为挂篮自重的1.1倍,而另一侧为挂篮自重的0.9倍;
(3)两悬臂端梁体浇筑不同步,两端混凝土浇筑体积差按5 m3计。
在桥梁施工过程仿真分析中,对桥梁有限元模型分别考虑上述非对称施工荷载,而后与风荷载加载工况进行荷载组合,分析非对称施工荷载下的结构静风安全,事实上当上述非对称施工荷载同时作用时,结构最为不利。虽然上述非对称施工荷载同时作用的概念较小,但基于偏安全的分析原则,在施工过程仿真计算中同时考虑了上述三种非对称施工荷载。
5.4.1 非对称施工荷载下位移结果分析
考虑非对称施工荷载后的桥梁最大悬臂阶段各节点位移结果见图11所示。
对比图9、图11的计算结果可知:非对称施工荷载对结构的竖向位移有显著的影响,由于施工荷载的不平衡,导致主梁整体在竖向发生了一定程度的倾斜。而非对称施工荷载对结构的横向位移几乎无影响,横向位移的大小主要由风荷载控制。风荷载引起的位移变化规律与对称施工荷载下的基本一致,龙卷风工况所引起的桥梁横向位移及竖向位移极值最大,其中主梁横向位移最大值为6.98 mm,竖向位移最大值为5.03 mm。
5.4.2 非对称施工荷载下应力结果分析
计算得到的考虑非对称施工荷载后,桥梁最大双悬臂阶段各风荷载加载工况下全桥各单元截面压应力最大值、最小值统计结果直方图见图12所示。
各关键位置在各风荷载加载工况中应力均为压应力,且满足规范限值要求。其中,主梁悬臂根部位置在各风荷载加载工况中压应力最大值为9.56 MPa,最小值为2.88 MPa;墩顶位置在各风荷载加载工况中压应力最大值为2.30 MPa,最小值为0.04 MPa;墩底位置在各风荷载加载工况中压应力最大值为2.65 MPa,最小值为0.39 MPa。
对比图10、图12的计算结果可知:非对称施工荷载主要影响主梁悬臂根部及桥墩部位的应力变化,对悬臂端部的应力影响较小。且在非对称施工荷载下,悬臂根部与桥墩部位的应力最大值均大于对称施工荷载下,应力最小值均小于对称施工荷载下,表明非对称施工荷载对结构应力有不利影响。风荷载引起的应力变化规律与对称施工荷载下的基本一致,悬臂根部、墩顶、墩底三个关键位置的应力最大值,最小值均出现在对称均匀风荷载加载工况。
6 结论
本文对比了采用CFD数值模拟得到的桥梁断面阻力系数和按照规范取定的阻力系数、偏安全地选用规范的阻力系数值求解作用于墩和主梁的静风荷载。考虑结构受力的不利情况,采用三种方式加载静风荷载,分别为对称均匀加载、非对称均匀加载和模拟龙卷风加载。为全面分析静风荷载作用下的桥梁结构安全性问题,分别采用了对称施工荷载作用和非对称施工荷载作用的最大双悬臂基准模型进行静风荷载加载。过分析和比较得到以下结论:
(1)采用“抗风规范”算得到的主梁的阻力系数CH大于采用CFD方法计算得到的阻力系数,表明“抗风规范”得到的阻力系数值更为保守。
(2)在最大悬臂阶段桥梁模型中,龙卷风工况所引起的桥梁横向位移及竖向位移极值最大,龙卷风工况对结构位移最为不利;各关键位置应力最大值,最小值均出现在对称均匀加载工况,对称均匀加载工况对结构应力最为不利。
(3)非对称施工荷载主要影响结构的竖向位移,而对结构的横向位移几乎无影响,横向位移的大小主要由风荷载控制。
(4)将对称施工荷载工况和非对称施工荷载工况分别与三种静风荷载加载工况进行组合,结果表明在各荷载工况下,桥梁各关键截面均处于全截面受压的状态,主梁悬臂根部最大压应力小于规范限值的要求。在对称施工荷载以及非对称施工荷载下的桥梁静风安全性满足要求。
参考文献:
[1]项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.
[2]BOONYAPINYO V, LAUHATANON Y, LUKKUNAPRASIT P. Nonlinear aerostatic stability analysis of suspension bridges[J]. Engineering Structures, 2006, 28(5): 793-803.
[3]程進, 江见鲸, 肖汝诚, 等. 风对桥梁结构稳定性的影响及其对策[J]. 自然灾害学报, 2002, 11(1): 81-84.
[4]杨玉浩. 高墩大跨连续刚构桥的抗风分析与研究[D]. 重庆: 重庆交通大学, 2017.
[5]王中秋. 壶口黄河大桥抗风稳定性措施研究[J]. 公路交通科技(应用技术版), 2014, 10(5): 285-287.
[6]郑一峰, 赵群, 暴伟等. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[7]韩万水, 陈艾荣, 马如进, 等. 高墩大跨刚构桥施工阶段的抗风分析[J]. 同济大学学报(自然科学版), 2007, 35(2): 166-170.
[8]徐庆超. 高墩大跨连续刚构桥悬臂施工阶段抗风安全性研究[D]. 西安: 长安大学, 2013.
[9]李建梅. 预应力混凝土连续梁桥悬臂施工中非技术手段误差分析[J]. 交通世界, 2020(11): 115-117.
[10]孔令智, 陈斌. 基于桥梁抗风稳定性桥位处基本风速的确定[J]. 公路交通科技(应用技术版), 2016, 12(3): 186-188, 213.
[11]交通运输部. 公路桥梁抗风设计规范: JTG/T D60-01—2004[S]. 北京: 人民交通出版社, 2004.
[12]瞿伟廉, 刘琳娜. 基于CFD的桥梁三分力系数识别的数值研究[J]. 武汉理工大学学报, 2007, 29(7): 85-88.
[13]易征. 连续刚构桥梁气动干扰效应数值模拟[J]. 交通科学与工程, 2018, 34(3): 20-26.
[14]王锋. 基于CFD对大跨度连续桥梁抗风性能分析[J]. 公路工程, 2018, 43(3): 83-86, 167.
[15]王洪顺. 基于CFD的人行悬索桥气动干扰效应数值仿真[D]. 保定: 河北大学, 2017.
(责任编辑:于慧梅)

