基于SIFT特征点的三维医学图像零水印算法


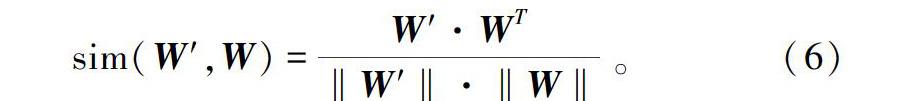
摘 要:为了在三维医学图像中隐藏病人的个人信息,并对该三维医学图像进行认证,提出了一种基于SIFT特征点的三维医学图像零水印算法,该算法既不会对原始的三维医学图像造成影响,又可以嵌入大容量的水印内容。首先,对三维医学图像进行切片并投影成二维图像;其次,对投影后的图像进行提升小波变换;再次,从小波低频系数中寻找SIFT特征点;最后选择纹理强的区域的SIFT特征点来生成特征向量,用于水印的嵌入。试验表明,该算法可以抵抗常规攻击和几何攻击,具有较强的鲁棒性。
关键词:三维医学图像;SIFT;零水印
中图分类号: TP309
文献标识码: A
数字医学图像作为医生判断患者健康状况及诊断病情的重要参考依据,在远程医疗中起着举足轻重的作用。在网络传输过程中,医学图像有可能被截获,记录在医学图像上的病人信息等敏感信息很容易泄露。数字水印技术是有效解决该问题的技术手段之一。尤其是研究如何在磁共振成像(magnetic resonance imaging,MRI)获得的三维医学图像中嵌入水印,实现三维医学图像的版权保护和病人信息的隐藏,意义重大。
文献[1]提出了一种基于整数小波变换的易碎水印算法,对医学图像进行整数提升小波变换,利用小波分解后的四叉树结构结合树节点上的统计信息和密钥来选择嵌入水印的位置。文献[2]提出了一种基于深度残差网络的医学图像鲁棒可逆水印算法,利用深度残差模型提取医学图像的深度特征信息,结合遗传算法和模糊C-均值的聚类算法对水印区域动态划分,根据聚类结果提取水印信息。文献[3]提出一种基于纹理度划分的医学图像可逆信息隐藏方法,对不同纹理度等级的像素采用不同的嵌入方法。文献[4]根据医学图像特征值的分布划分感兴趣区域,将认证水印嵌入到感兴趣区域轮廓波分解后的低频子带的最大奇异值中,病人信息嵌入到非感兴趣区域轮廓波分解后的中频子带系数中。文献[5]将医学图像进行离散小波变换,从小波低频系数中寻找图像的特征点,通过特征点计算出纹理复杂的区域,即为医学图像的感兴趣区域,进行水印嵌入。基于变换域的水印算法,因为良好的鲁棒性,一直是研究的热点[6-8]。
目前,数字水印技术在三维医学图像上应用还比较少。文献[9]提出一种基于单向预测误差扩展的三维医学图像可逆水印算法,结合MRI图像的特征,采用单向直方图位移与预测误差扩展相结合的方法实现信息嵌入。文献[10]对三维医学图像进行三维离散余弦变换(three dimensional discrete cosine transform,3D-DCT),从低中频系数中得到视觉特征向量来进行水印的嵌入与提取。文献[11]对文献[10]的算法进行改进,通过混沌加密技术对水印进行预处理来提高水印信息的安全性。由于DCT变换后,重要的信息都集中在DCT变换的低中频系数中,只占了一小部分系数,其他系数在图像压缩处理中会被抛弃或进行量化以减小数据量。一个系数只能嵌入一个bit的水印,因此在实际使用过程中,水印的长度不能太长,水印容量会受到限制。
本文对数字水印技术在三维医学图像中的应用进行研究,提出一种零水印方案。利用尺度不变特征变换(scale invariant feature transform,SIFT)特征点具有对噪声不敏感、协变于几何变换、且具有一定的局部性的特点, 来实现水印的嵌入。试验结果表明,该算法在抵抗常规攻击和几何攻击中取得了很好的效果。
1 SIFT
SIFT算法由LOWE于1999年提出,2004年完善总结。这是一种提取局部特征的算法,在尺度空间寻找极值点,提取位置、尺度、旋转不变量,满足KUTTER等人[12]于1999年提出的第二代数字水印技术的性质要求。
算法首先在尺度空间上进行特征检测,并确定特征点(keypoints)的位置和特征点所处的尺度,然后使用特征点邻域梯度的主方向作為该点的方向特征,生成一个128维的特征描述子[13]。在这个特征描述子中,滤除大于0.2的梯度值,然后重新归一化。以此弱化梯度大小的作用而强化方向信息的作用。0.2是LOWE在试验中得出的经验值。
2 提升小波变换
提升小波变换(lifting wavelet transform,LWT)由Swelden于1997年提出,被称为第二代小波变换,比第一代小波变换更加快速有效。它继承了第一代小波的多分辨率特征,但不依赖于傅里叶变换,是一种空域方法,却能取得与第一代小波变换相同的特性。另外,还具有以下优良的特征:结果简单、运算量小;原位运算,节省存储空间;可逆的整数到整数变换,便于实现。
使用LWT分解信号涉及三个基本步骤[14]:
(1)拆分:将输入信号划分为不重叠的奇样本和偶样本。
(2)预测:偶样本和奇样本之间的相关性意味着任何一个都可以作为另一个的预测器。通常用偶样本来预测奇样本,通过与原奇样本的差值,来确定高频分量。
(3)更新:更新后的高频分量与原偶样本相加来确定低频分量。
3 水印嵌入步骤
3.1 从三维医学图像投影成二维图像
要把三维医学图像投影成二维图像,可以选择横截面、冠状面、矢状面、或者其他合适的角度,对三维医学图像进行切片,给每个切片Si赋予一个权值wi,要求wi为非负整数,则投影后的二维图像I的计算公式为:
权值所组成的数列(w1,w2,…,wn)可以作为密钥,提高算法安全性。
3.2 对图像作LWT变换,提取低频分量LL
为了保证水印算法的鲁棒性,水印应放在对视觉系统感觉上最重要的分量上。图像经过提升小波变换,其低频分量系数保留了绝大部分的信息和能量[15],低频分量系数比高频分量系数具有更大的容量[16],而且嵌入低频分量系数的水印在图像进行JPEG等有损压缩的操作中具有更强的鲁棒性。
对投影后的二维图像I作LWT变换,得到图像的多分辨表示:LL,LH,HL,HH。从低频分量LL系数矩阵中提取特征点,既保证水印有足够的鲁棒性,又可以提高特征提取的速度。
3.3 提取SIFT特征点
从低频分量LL中提取出SIFT特征点,再从中选取若干个特征点以生成图像的特征向量。
在SIFT特征点的提取过程中,会有15%的特征点被赋予多个方向[13],这些特征点在特征点匹配中具有更高的稳定性。将有多个方向的特征点所构成的集合记做K1,只有一个方向的特征点所构成的集合记做K2。首选K1中的特征点来生成特征向量。
SIFT特征点的尺度具有缩放不变性,它的值代表图像被平滑的程度,大尺度对应着图像的近似信息,小尺度对应着图像的细节信息。与小波变换类似,选取大尺度的特征点来生成特征向量,具有较好的鲁棒性。
SIFT特征点对应于图像中的像素突变点,特征点数目越多的地方,往往纹理越强,纹理复杂区域即为该医学图像中的感兴趣区域,也就是医疗诊断中的病灶区。选取病灶区的特征点来生成特征向量,具有较好的鲁棒性,不用担心会丢失该特征点。因为一旦该区域被剪切掉,该医学图像就失去了意义。
为了综合考虑尺度和纹理特征,采用公式(2)得到邻域半径:
式中,s表示特征点的尺度,λ是常量,可用来控制邻域半径的大小。
计算每个特征点在邻域半径所覆盖范围内的特征点数,按照特征点数量从大到小的顺序,对特征点进行排序得到队列Q,其中K1的顺序在K2的前面。
若要嵌入L个bit的水印,则按照从前到后的顺序,从队列Q中取出「L/128个特征点以生成图像的特征向量,「代表上取整。
3.4 生成图像的特征向量
3.5 水印的嵌入
4 水印提取步骤
本算法水印提取过程与水印嵌入过程类似。
具体步骤如下:
(1)根据切片的方式和权值数列(w1,w2,…,wn),将待测的三维医学图像投影为二维图像;
(2)对上述二维图像进行LWT变换,提取出低频分量LL;
(3)从LL中提取出SIFT特征点;
(4)利用嵌水印时保存的描述子D,寻找与之匹配的特征點,得到待测图像的特征向量V;
(5)将二值序列K与待测图像的特征向量V进行异或运算,得到待测图像的水印W;
(6)通过计算待测图像的水印W与原始水印W的相似度,并与阈值T作比较,来判别水印是否存在。若相识度高于阈值,则认为水印存在;否则水印不存在。这里采用相关系数进行相似度的定量评价,计算公式为:
5 仿真试验
为了验证上述水印算法的有效性,使用MATLAB R2017b进行仿真,原始三维医学图像是MATLAB自带的一个MRI图像,如图1所示。试验首先生成1 000组独立的二值伪随机序列(取值为0或1),每组长度128位,选取第500组作为水印序列,代表病人的信息。在不加干扰的情况下,水印检测结果为图2所示,横轴代表1 000组独立的二值伪随机序列,纵轴代表它们与水印的相似度sim,从图中可以明显看出,非水印序列与水印序列的相似度在0.7以下,因此试验中取0.7作为阈值T。
为了证实本算法的有效性和鲁棒性,在试验中对原始三维医学图像分别进行一系列的常规攻击和几何攻击,例如加入高斯噪声、JEPG压缩处理、旋转、尺度缩放、剪切等。试验结果见表1—5。
从表1、表2、表3、表5看出,本算法在噪声攻击、JPEG压缩攻击、旋转和剪切攻击等攻击下,提取出的水印与原始水印的相似度都在0.92以上,说明本算法对这些攻击有非常好的鲁棒性。
在表4中,当原三维医学图像缩小为原来的一半(缩放比例为0.5)时,图像变得比较模糊,此时提取出的水印与原始水印的相似度较低,但仍然高于设定的阈值0.7,仍能检测出水印。其他缩放比例下提取出的水印与原始水印的相似度都高于0.98,可以检测出水印。因此,本算法对缩放攻击有较好的鲁棒性。
综上所述,本算法对常规攻击和几何攻击,具有很好的鲁棒性。
6 结论
本文提出了一种基于SIFT特征点的三维医学图像水印算法,是一种零水印方案,不会对原三维医学图像产生影响。算法将三维医学图像投影为二维图像,既起到了加密的作用,又减少了计算量。考虑到小波域在抵抗JPEG压缩中的优良特性,从LWT变换后的小波低频分量中选择特征点,同时,自动定位到该医学图像的病灶区,从病灶区中提取出的特征点具有更强的鲁棒性。一个特征点所生成的特征向量就可以嵌入128 bit的水印,一副医学图像存在多个特征点,因此,本算法有较高的水印嵌入容量。
参考文献:
[1]冯前进, 陈凌剑, 杨丰. 基于整数小波变换的医学图像易碎水印方法[J]. 中国图象图形学报, 2006, 11(5): 736-741.
[2]李智, 周旭阳, 殷昕旺, 等. 基于深度残差网络的医学图像鲁棒可逆水印算法[J]. 贵州大学学报(自然科学版), 2020, 37(3): 58-68.
[3]才雪, 杨杨, 肖星星. 基于纹理度划分的医学图像可逆信息隐藏方法[J]. 计算机应用, 2018, 38(8): 2293-2300.
[4]陈青, 宗偲琦. 用于医学图像认证的Contourlet-SVD双水印算法[J]. 小型微型计算机系统, 2019, 40(1): 207-211.
[5]沈炎斌. 基于图像特征的医学图像水印算法[J]. 三明学院学报, 2015, 32(6): 37-40.
[6]ZHENG P, HUANG J. Discrete wavelet transform and data expansion reduction in homomorphic encrypted domain[J]. IEEE Transactions on Image Processing, 2013, 22(6): 2455-2468.
[7]ZHAO B, KOU W, LI H, et al. Effective watermarking scheme in the encrypted domain for buyer-seller watermarking protocol[J]. Information Sciences, 2010, 180(23): 4672-4684.
[8]GUO J, ZHENG P, HUANG J. Secure watermarking scheme against watermark attacks in the encrypted domain[J]. Journal of Visual Communication & Image Representation, 2015, 30: 125-135.
[9]李琦, 顏斌, 陈娜, 等. 基于单向预测误差扩展的三维医学图像可逆水印算法[J]. 计算机应用, 2019, 39(2): 483-487.
[10]LI J, DU W, BAI Y, et al. 3D-DCT based zero-watermarking for medical volume data robust to geometrical attacks[J]. Wireless Communications and Applications. 2012 (72): 433-444.
[11]刘瑶利, 李京兵. 基于3D-DCT和混沌加密的医学体数据多水印算法[J]. 计算机工程与设计, 2014, 35(1): 26-31.
[12]KUTTER M, BHATTACHARJEE S K, EBRAHIMI T. Towards second generation watermarking schemes [C]//International Conference on Image Processing. Kobe: IEEE, 1999: 320-323.
[13]LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[14]DAUBECHIES I, SWELDENS W. Factoring wavelet transforms into lifting steps[J]. Journal of Fourier Analysis and Applications, 1998, 4(3): 247-269.
[15]MEHTA R, GUPTA K, YADAV A K, et al. An adaptive framework to image watermarking based on the twin support vector regression and genetic algorithm in lifting wavelet transform domain[J]. Multimedia Tools and Applications, 2020, 79: 18657-18678.
[16]黄达人, 刘九芬, 黄继武. 小波变换域图像水印嵌入对策和算法[J]. 软件学报, 2002, 13(7): 1290-1297.
[17]BAS P, CHASSERY J M, MACQ B. Geometrically invariant watermarking using feature points[J]. IEEE Transactions on Image Processing, 2002, 11 (9): 1014-1028.
(责任编辑:于慧梅)

