深度体验实验过程,深刻理解实验本质
黄城红 刘咏梅
一、现象
“可能性”是人教版数学五年级上册的教学内容。在教学这节课时,很多教师都会做抛硬币实验,让学生体验事物发展的可能性及说明概率的大小。在教学中,我们经常会见到如下的教学过程:学生分小组抛硬币,以同桌的两个人为一组,一个抛,一个记录,当抛了10次后,各小组汇总,统计全班的实验结果,得到结论:每抛一次硬币,正面和反面都有可能出现。从每一个小组统计的结果来看,正面和反面的次数相差可能会比较大,也可能比较相近,感觉没有规律,如果把全班的统计结果相加,则正、反面出现的次数就比较接近。教师再出示历史上一些数学家所做的抛硬币实验的有关材料(如表1),强调当抛硬币的次数越多时,正、反面各出现的概率会越接近[12],也就是50%。
二、反思
在这个教学过程中,笔者觉得有如下几个方面值得商榷。
1.学生的操作不够规范
要体现硬币正、反面出现的随机性,那就要求用统一的硬币,在抛起的过程中,能够翻滚较多的次数,这样,硬币落在桌面上出现正、反面就会更具有随机性。但在实验过程中,有些教师没有规范抛硬币的动作,学生抛硬币的动作就会五花八门,有的学生只是把硬币拎到大概30 cm的高度就松手,让硬币自由地落下,没有向上抛的动作。这样,硬币在有限的时间和空间内,没有翻滚或只翻滚一两次就落在桌面上,就不能体现随机性。
2.学生对可能性的体验不深
学生只是在教师的要求下进行抛硬币的实验,做完实验后,也只是汇报数据,没有对实验的过程和结果进行反思,也没有对数据进行分析,这样就只是纯粹为做实验而做实验。这个过程就好像蜻蜓点水,太快、太浅,一滑而过,没有触及数学的本质。表面看起来学生都在进行抛硬币操作实验,很热闹,学生也都参与进来了,但在这种热闹的背后却是数学味不足,没有蕴含数学思考。
3.对硬币正、反面出现的概率理解有偏差
当抛的次数越多,硬币正、反面出现的概率就越接近50%吗?这样的表述是否正确?把历史上一些数学家做的硬币实验拿出来比较,是否具有可比性?
对于硬币正、反面出现的概率,我们都知道,各是50%,于是就想通过实验来证明。实际上,这个概率是不需要证明的,而且是证明不了的。比如在做1万次实验时,恰巧得到硬币正、反面各是5 000次,就能说得到这个结论了吗?不一定,因为如果在这基础上再做一次,又不是50%了。所以,从某种程度来说,这是一个不可能经过实验能证明得到的结论。既然得不到结论,为什么还要去做这个抛硬币的实验呢?
我们做这个实验,不是要刻意地追求概率是50%的结果,而是要体验50%的大概存在,体验这个实验的过程。因为这个概率50%是由这个实验的本质所决定的:只要把同一枚硬币从同一个高度抛,在空中有足够多的翻滚次数,这个实验本身就决定了硬币正、反面出现的概率是50%。而我们做实验时,记录的只是硬币正、反面出现的频率,这个频率是可以经过实验统计而得到的,这个频率只是这个概率50%的外在表现形式,这个频率也只是表现这个实验的本质。所以,我们做实验统计的只是频率,通过这个统计到的频率去推测概率,感知概率,而不是去证明它。
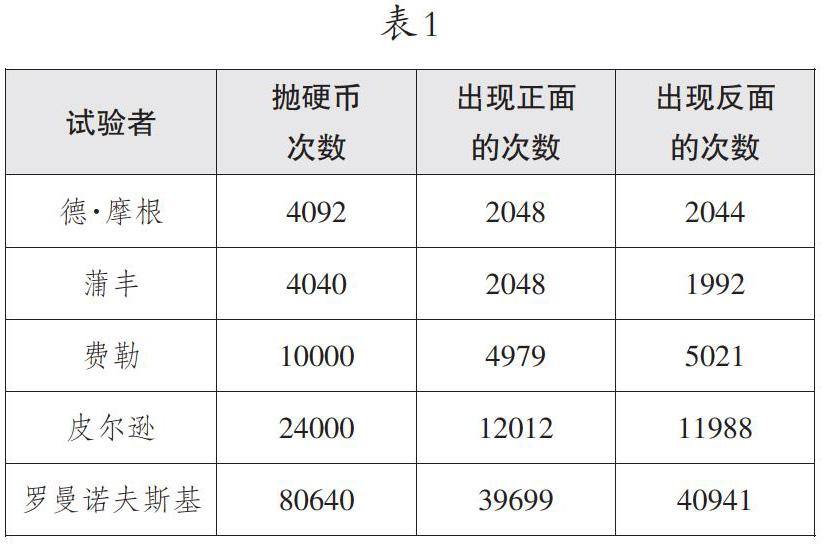
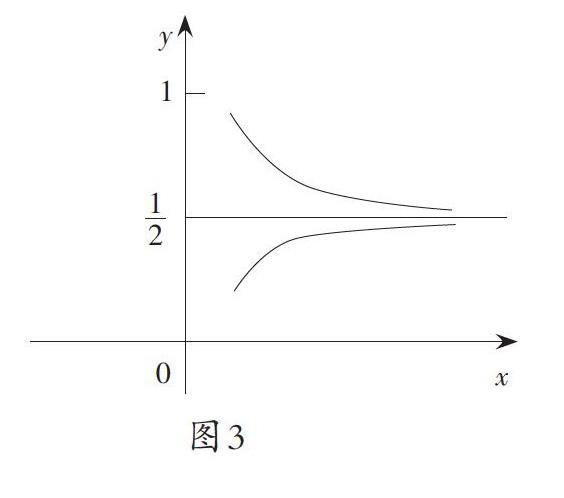
对于硬币正、反面出现的概率问题,还应该这样理解:这个实验的本身就决定了50%的概率,如图1中的那条表示[12]的横线,而我们做抛硬币出现的正、反面的概率,就是围绕这条[12]的横线上下波动的一条毫无规律的曲线,这条曲线在局部看时,可能会波动比较大,但做的实验次数更多时,从整体看,这条曲线就会钝化,波动也就没有那么剧烈了,就会更接近于50%了。图2的这条股票K线,当交易日较少时,看起来波动的范围比较大,而当交易日比较多时,此时就要看股票月K线,就感觉波动不大了,所以我们在总结实验结论时,不能说成是当抛硬币的次数越多,概率就越接近50%,因为如果这样表述,画出的图像就应该是图3这样,这是不符合这个实验的本意的。
另外,在累加學生的实验次数之后,再与历史上的数学家所做的实验进行对比,这样做科学吗?科学家也是在做抛硬币实验,但他们用的硬币与我们所用的硬币是一样的吗?我们之所以用硬币来做抛投实验,就是因为取材方便,场地要求也不高。但我们都知道,硬币只是近似的矮圆柱体,但每个国家硬币的底面直径和高度都不同,在硬币上雕刻的花纹也不同,不同硬币的重心会稍微有些不同,这样做出来的实验结果当然不同。所以,在抛不同硬币时,有些硬币正面出现的概率可能会比50%稍微多一些,而有些硬币正面出现的概率就会比50%少些。从理论上来说,抛不同的硬币,就属于不同的实验,是不具有可比性的。
三、实验的再处理
为了让学生更好地体验这个实验的本质,我们可以重新处理这个实验过程。
全班用统一的硬币。我国现行常用的硬币有1元和5角两种,其中5角硬币偏轻、偏小,相比较,全班统一用1元硬币较为合适。
先猜测实验的结果。根据生活经验,学生能猜到硬币正、反面出现的概率是相等的。
让学生自己设计抛硬币实验的方案。有了猜测,就必须用实验来验证。如何做这个实验呢?教师可以让学生自己设计和讨论。学生在讨论中,就会出现各种抛硬币的方法,通过比较和辨析,明确要求把硬币举到统一高度(例如40 cm),再往上抛,让硬币有充分多的翻滚次数,这样才能体现这个实验的随机性;学生也会认识到,做一次实验不具有代表性,做的次数越多就越具有统计意义,但要在课堂上做比较多的次数,时间又有限,于是,学生分组做10次实验后,各组再把结果累加。学生在讨论实验方案过程中,就已经初步感知这个实验的目的就是要突出随机性,也知道要证明猜测的正确性,实验方法必须正确,而且要有大量的实验数据来验证,这也培养了学生理性的科学精神,学生体会到正确的实验方法的重要性,为今后的学习和研究渗透了良好的科学研究精神和态度。
为了让学生更好地体会随机性,教师可以利用表2。从表中可以看出,在每次抛硬币之前,教师都要求学生猜测结果,再与每次的实验结果进行对比。增加这个猜测环节,可以让学生充分感受到这个实验的结果是很难猜测到的,是不受人为控制的,是无序的,从而更深刻地体会硬币正、反面出现的随机性,从而更好地感受可能性的本质。
这个实验,不需要教师把结论告诉学生,而是要让学生在自己实验的基础上发现规律和总结规律,让学生自己把实验过程中的感受说出来,这才是这个实验最需要得到的东西。
教师还可以让学生在课后做同时抛两枚硬币的实验,记录实验结果。让学生思考:各会出现什么情况?每种情况出现的频率大概是多少?让学生在实验中发现规律、总结规律,学生也会很热衷于做这样有趣的实验。
从以上可以看出,学生在这个抛硬币的实验过程中,不应只是一个按教师指令进行抛硬币的操作者,也不是一个被告知结果的接受者,而应该是一个具有充分自主学习能动性的实验者和探究者。丰富的实验内容可以让学生在实验过程中有更充分的探究和体验。经过这样的实验过程,学生对于随机性、可能性的感受将会更加深刻,也更能理解概率的概念,同时还能培养严谨的科学研究精神,提升数学综合素养。
(作者单位:江西省南昌市铁路第一小学 江西师范大学数学与统计科学学院)
投稿邮箱:405956706@qq.com

