基于ANSYS Workbench的高空飞翔极限风载荷计算

赵九峰，马 宁，张劲松

(1.河南省特种设备安全检测研究院，河南 郑州 450000；2.中国特种设备检测研究院，北京 100029)

0 引言

风载荷是大型游乐设施设计的重要计算载荷，关系到游乐设施的稳定性、安全性。在大型游乐设施的设计计算和施工过程中，应全面把握风载荷的影响，以确保乘客和设备的安全。所以国家相关规范中要求，大型游乐设施设计文件、鉴定文件需包含关于极限风载荷工况下主要受力部件的强度校核[1]。

高空飞翔是安装在室外的大型游乐设施，是飞行塔类游艺机中的一个品种[2]，具有大长宽比的高耸钢结构，风载荷对设备的影响不可忽略。因此，分析研究高空飞翔在风载荷作用下的应力响应，对确保高空飞翔的安全具有重要的意义。

1 风载荷计算参数

本文以32 m高空飞翔为计算对象，它主要是由塔体、配重和提升臂架等几部分组成，主体结构为钢结构，材料为Q235B(屈服强度σs=235 MPa)。塔体立柱宽度为B=1.5 m，高度H=32 m(不包括避雷针)，基本自振周期T=0.4 s，提升臂架的轮廓面积为S1=2 m2，高空飞翔的结构简图如图1所示。

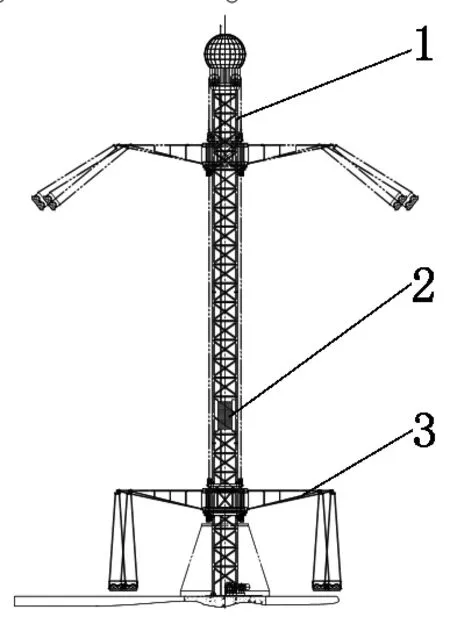
1-塔架部件；2-配重部件；3-提升臂架部件

根据GB8408—2018《大型游乐设施安全规范》中6.1.2.10规定：风载荷分为正常使用工况载荷和极限工况载荷，风载荷的取值及计算方法按照GB50009中的规定执行[3]。由《起重机机械金属结构》：计算风载荷时，认为它是一种任意方向作用的水平力，极限工况风载荷是非工作情况下受到的当地最大计算风载荷[4]。

根据GB50009—2012《建筑结构荷载规范》8.1.1：计算主要受力结构时，垂直于设备表面上的风荷载标准值[5]为：

wk=βzusμzw0.

(1)

其中：wk为风荷载标准值,kN/m2；βz为高度z处的风振系数；us为风荷载体型系数；μz为风压高度变化系数；w0为基本风压值,kN/m2。

由《起重机设计规范》表19可知:计算非工作状态风载荷时，可沿高度划分成10 m高的等风压段进行计算，也可取结构顶部的计算风压作为设备全高的定值风压[6]。保守计算，本文不对高空飞翔全高分段计算风压，按照全高定值风压去计算校核极限工况风载荷的各个计算参数。

1.1 基本风压值w0

风速与风压的关系为[7]：

(2)

其中：v为计算风速,m/s。

游乐设施的设计，按最大运行风速15 m/s计算正常使用工况下的风载荷，则游乐设施工作状态下的风压值为w0=0.14 kN/m2。

极限工况风载荷是游乐设备在不工作时能承受的最大风力作用，以当地比较空旷平坦的地面上离地10 m高，统计所得的50年一遇10 min平均最大风速为标准计算基本风压。按照《起重机设计规范》表18可知:我国非工作状态风压的取值，内陆的华北、华中和华南地区取w0=0.5 kN/m2，内陆的西北、西南、东北和长江中下游等地区取w0=0.6 kN/m2，沿海地区取w0=0.6 kN/m2～1.0 kN/m2，以上海为界，上海地区取w0=0.8 kN/m2，上海以北取小值，以南取大值。

综上可知，游乐设施在极限工况风压取w0=0.8 kN/m2可以覆盖我国大部分地区，因此本文按此值校核高空飞翔在极限工况风载荷下的受力情况。

1.2 风振系数βz

风对设备的作用是不规则的，风压随风速、风向的变化而不停地改变。实际工程使用中，游乐设备结构上的风荷载可分为两种成分：平均风和脉动风。平均风压使设备产生一定的侧移，而脉动风压使其在该侧移附近左右振动[8]。目前采用加大风荷载的办法来考虑这个动力效应，在风压值上乘以风振系数[9]。

对于低矮、刚度比较大的结构，脉动风压引起的结构振动效应比较小，一般不需要考虑脉动风振作用，而仅考虑平均风压作用。对于30 m以下且高宽比小于1.5的结构，风振系数取βz=1.0[10]。对于高度较大、刚度较小的游乐设施，脉动风压会产生不可忽略的动力效应；高度大于30 m、高宽比大于1.5的高耸结构，需考虑脉动风振作用。

根据GB50135—2019《高耸结构设计标准》4.2.9：高耸结构在z高度处的风振系数为：

βz=1+ξε1ε2.

(3)

其中：ξ为脉动增大系数；ε1为风压脉动和风压高度变化等的影响系数；ε2为振型、结构外形的影响系数。

脉动增大系数与设备基本风压、自振周期T和阻尼比有关，按表1取值。

表1 钢结构脉动增大系数ξ

高空飞翔w0T2=0.13 kN·s2/m2，由表1通过插值计算，可得脉动增大系数ξ=1.9。

风压脉动和风压高度变化等的影响系数与设备的高度和地面的粗糙度类型有关，地面的粗糙度分为4类，游乐设施多分布在城市郊区，为B类粗糙度，ε1按表2取值。

表2 风压脉动和风压高度变化等的影响系数ε1

由高空飞翔H=32 m，由表2通过插值计算，可得风压脉动和风压高度变化等的影响系数ε1=0.81。

振型和结构外形的影响系数与设备的相对高度、顶部与底部的相对宽度有关，按照《高耸结构设计标准》表4.2.9-2可得ε2=1.0。

将相关参数代入式(3)可得高空飞翔的风振系数：βz=2.54。

1.3 体型系数us

体型系数也称空气动力系数，它是风在工程结构表面形成的压力(或吸力)与按来流风速算出的理论风压的比值。它反映出稳定风压在工程结构表面上的分布，并随结构的形状、尺度以及气流方向等而异[11]。体型系数与设备的挡风系数和结构型式有关。

挡风系数φ可按照下式计算：

(4)

其中：A0为结构净投影面积,m2；A为迎风面轮廓面积,m2。

根据高空飞翔塔体结构图纸，经计算挡风系数为0.2。主体结构由不同型号的方管焊接而成，因此可类比《建筑结构荷载规范》表8.3.1中第33项来计算体型系数。

(5)

其中：μst为方管体形系数，值为1.3；n为榀的数目，塔体前后共2榀，值为2；η为折算系数，值为0.85。

将相关参数代入式(5)计算，得塔体的整体体形系数μs=0.48。

1.4 风压高度变化系数μz

设备所承受风压大小随高度的增加而加大。为了反映这个事实，计算风载荷时，包含有这个反映高度效应的系数，其变化规律与设备高度和地面粗糙度有关。按照B类粗糙度，风压高度变化系数可按表3取值。

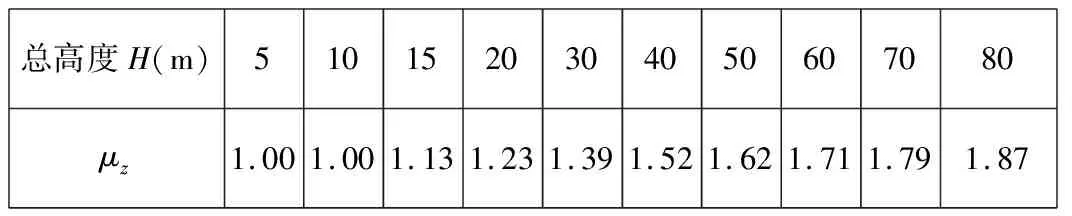
表3 风压高度变化系数μz

高空飞翔H=32 m，由表3通过插值计算，可得μz=1.4。

1.5 极限风载荷

由公式(1)可得：wk=2.54×0.48×1.4×0.8=1.4 kN/m2。

高空飞翔迎风面的轮廓面积为：

A=BH+S1.

(6)

将相关参数代入式(6)计算得A=50 m2。

高空飞翔在极限风载工况下受到的等效水平力为：

F=wkA.

(7)

将相关参数代入式(7)计算得F=70 kN。

2 有限元分析

高空飞翔在极限风载荷工况下，仅受到重力作用和极限风载荷的水平力作用，为了保证整体结构具有足够的强度，利用ANSYS Workbench有限元分析软件对其进行静力学分析，在极限风载荷工况下，提升臂架部件放置在塔体底部，采用2节点的梁单元(BEAM188)[12]，建立有限元模型如图2(a)所示。

塔体立柱底部固定在基础上，故底部施加固定约束(Fixed)。考虑自重的影响，整体施加9.8 m/s2的向下重力加速度，塔体和提升体一侧施加70 000 N的水平载荷。座舱、配重等部件采用MASS21质量单元，附加在整体结构相应位置上，载荷与约束如图2(b)所示。

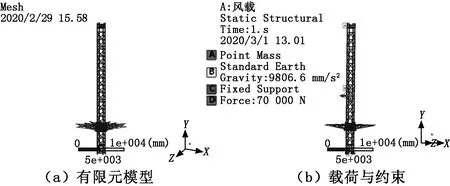
图2 高空飞翔模型与载荷

在重力载荷和极限风载荷作用下进行静力分析，求解成功后进入后处理得到，高空飞翔应力云图如图3所示，应力最大值为113 MPa，出现在塔体根部。

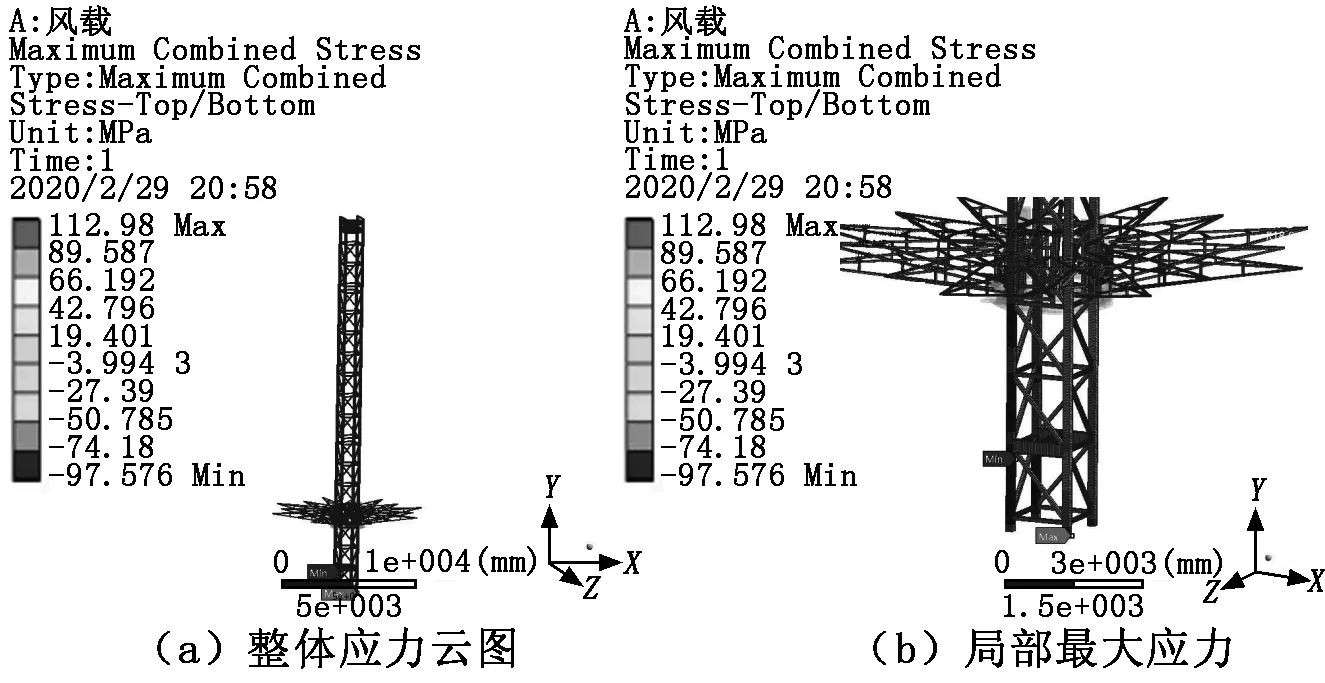
图3 高空飞翔应力云图

3 结论

本文以某32 m高空飞翔为工程背景，利用有限元仿真软件ANSYS Workbench对高空飞翔整体结构在极限风载荷工况下进行模拟分析计算，计算结果表明：在极限风载荷作用下，高空飞翔主体结构未发生永久变形，即结构的最大应力未达到屈服强度。这表明高空飞翔能安全地抵御50年一遇的风载荷影响，保证设备能够安全地运营，其计算方法和结果为其他大型游乐设施风载荷的计算提供了参考。