二自由度云台控制系统设计及控制方法的研究*
赵 炯,谢正东,周奇才,熊肖磊
(同济大学 机械与能源工程学院,上海 201804)
0 引言
云台在实际应用中主要起到稳定设备的作用,根据所搭载设备的需要,云台既可以安装在固定平台上也可以安装在移动平台上[1],在监控安防[2-3]、机器人[4-5]、无人机[6]等许多领域都需要二自由度云台的稳定控制。如机器人伺服控制和军事装备控制等应用场景对于二自由度云台的控制提出了较高的要求,能够实现快速响应并能进行目标稳定跟踪的云台有着较高的应用价值。
本文设计了一种二自由度云台控制方案,基于二自由度云台实验平台,采用系统辨识构建控制模型,进行了串级双环控制器的设计和仿真,最后将控制方法应用到实验平台上进行了遥控实验和定位实验,实现了云台的稳定控制,并与视觉识别相结合,进行了目标跟踪实验。
1 二自由度云台控制系统方案
二自由度云台机械机构如图1所示,其具有Pitch(俯仰角)和Yaw(偏航角)两个方向上的自由度,除此之外还搭载有摄像头、图传等其他传感器模块。

图1 二自由度云台机械结构
1.1 控制系统硬件方案
整个云台系统的控制方案分为硬件部分和软件部分,其中硬件框图如图2所示。控制信号来自于遥控信号和上位机通信两部分,在不同模式下处理不同的控制信号。数据反馈即云台的姿态数据来源于陀螺仪数据读取。执行信号经CAN通信分别到达Pitch轴和Yaw轴电机的驱动器并最终驱动电机转动。
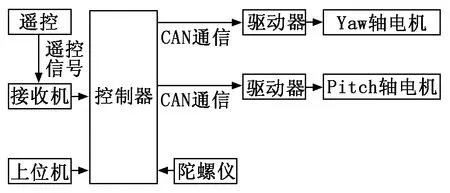
图2 云台硬件框图
1.2 控制系统软件方案
云台下位机控制的程序框图如图3所示。首先对于一些外设硬件和控制器进行初始化,之后进入定时器主循环,在一次程序循环中,先进行姿态数据的读取和遥控信息处理,根据遥控信息来进行云台控制模式判断,根据不同模式进行不同的指令处理,最终进行云台的控制,一次循环结束,返回姿态信息处理。对于云台的下位机系统来说,分为4个模式,分别是跟踪模式、遥控模式、定位模式和待机模式。在跟踪模式下,控制器接收图像处理的目标位置;在遥控模式下,控制器对遥控信息进行处理;在定位模式下,控制器处理来自上位机的指令;在待机模式下,保持停转。
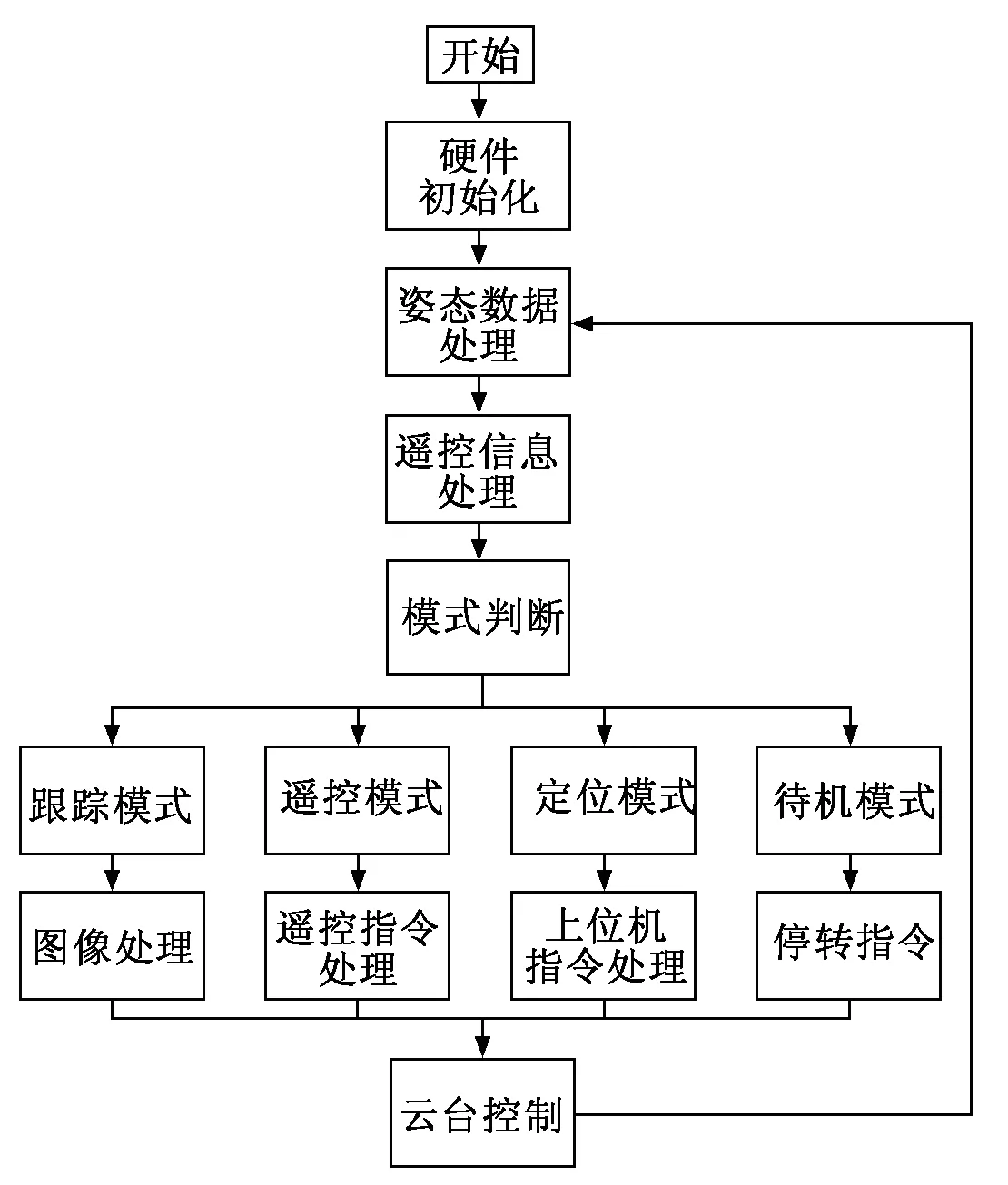
图3 云台控制程序框图
2 云台数学模型的建立
对于云台系统来说,需要具有精度高、动态性能好、抗干扰能力强的闭环控制[7],因此本文在初步确定了串级PID(比例、积分、微分)双闭环控制方案后,可以得到其基本的控制框图如图4所示,即给定目标角度后,经过校正环节转换为对应的电流,输入到驱动器,再由驱动器驱动电机输出一定角速度,经过积分环节输出角度,输出的角度反馈到比较元件。

图4 云台控制模型框图
本文采用系统辨识法来进行云台数学模型的建立,由图4可以看出,主要需要辨识的是从电流输入到角速度输出的执行环节。
2.1 确定模型结构
根据先验知识可以初步确定系统的一些特征。在设计云台时已经考虑到质量对于云台控制的影响,使云台质心与Pitch轴和Yaw轴的中轴线重合,并且轴系均采用轴承支承,可以近似认为云台的两轴各为一个单轴的电机拖动系统,耦合性低。根据无刷直流电动机的特性,电机转矩与电流基本为正比的线性关系,则转矩与电流的关系为:
(1)
其中:Tm为电机的电磁转矩;Id为电流;KE为与电机结构有关的常数;KT为电机的转矩系数。云台质心处于轴线上,则可以考虑忽略负载转矩TL,并且无储能元件,考虑到可能存在的低阻尼,对于单轴转动可以得到运动方程式如下:
从女人口中得知,赵晓峰很有技巧,一心扑在事业上的何冰完全没有察觉,而这也是令那女人不爽的原因之一:费力气掩饰,说明赵晓峰还不想跟何冰分手。
(2)
其中:J为该系统的转动惯量;ω为转速;t为时间;c为阻尼。可以认为该环节为线性一阶惯性环节,其传递函数为:
(3)
其中:K为比例常数;T为过渡时间。
由于阻尼低到可以忽略不计,该环节近似一个积分环节。以转动角度为输入和输出时,整个系统接近为二阶线性时不变系统。
2.2 实验设计
根据确定的模型结构可知,以速度作为输出时,系统接近一个一阶环节,同时考虑到实际信号输入和输出数据的采样难度,本文采用输出数据变化较为平缓的阶跃响应法。
对于速度输出的一阶环节的输入信号是直接给定的电流值,取采样频率为HG900电调的CAN最高通信频率1 kHz。
2.3 数据采集与预处理
基于实验的输入信号设计和采样频率设计进行实验,由上位机读取陀螺仪姿态数据,得到初步响应测量数据。由于陀螺仪的零点漂移会造成系统测量误差,而同一系统下,对于同一阶跃信号的多次响应,测量还存在着随机误差,因此需要针对这两种测量误差分别做数据预处理。
云台静止时,Picth轴角速度测量的零点漂移为-0.221 946 °/s,Yaw轴角速度测量的零点漂移为-0.024 475 °/s,在所有测量数据上进行系统误差补偿。
当消除系统误差后,为消除随机误差,将两轴系统各自的响应测量数据在同一时间轴下进行均值化处理。
2.4 参数估计
在一阶惯性结构下获得的Pitch轴的辨识环节的传递函数为:
(4)
根据模型分析可以判断该环节中阻尼非常小,对此可以再用积分结构进行辨识,得到的传递函数为:
(5)
获得的Yaw轴的辨识环节的传递函数为:
(6)
2.5 模型检验
选用离线数据检验方法进行模型验证,对Picth轴和Yaw轴进行参数估计后,所确定的系统模型的阶跃响应与建模数据的拟合度分别达到了95.63%和98.89%。按照相同的数据预处理方法,对Picth轴和Yaw轴分别重新采样一组检验数据,其与辨识环节的阶跃响应对比曲线分别如图5~图7所示。
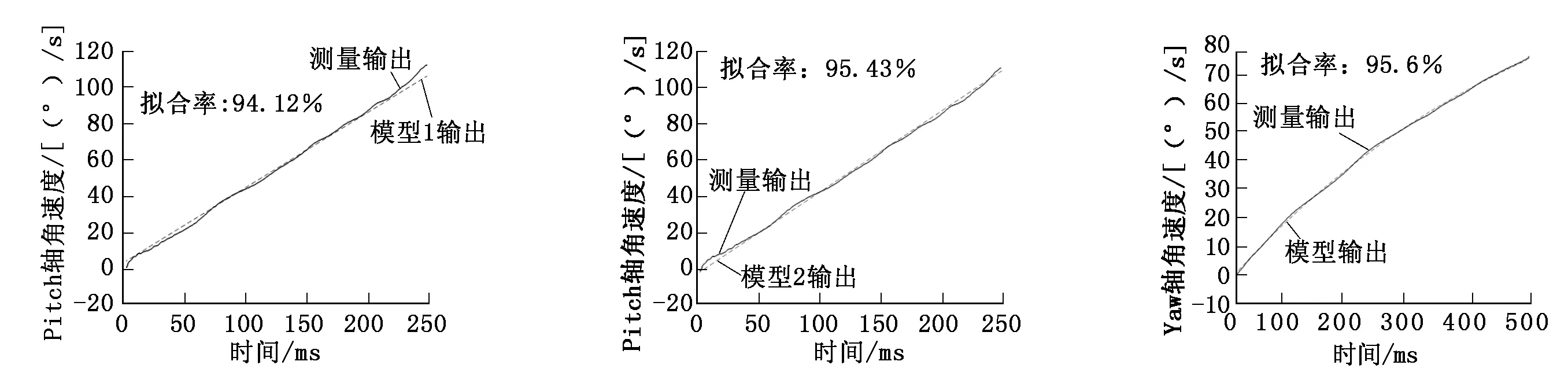
图5 Pitch轴系统辨识环节模型1验证 图6 Pitch轴系统辨识环节模型2验证 图7 Yaw轴系统辨识环节验证
在Picth轴系统辨识环节验证中,模型1为一阶惯性结构,拟合度为94.12%;模型2为积分结构,拟合度为95.43%。在Yaw轴系统辨识环节验证中,模型结构为一阶惯性结构,拟合度为95.6%。
2.6 最终结果
根据以上系统辨识过程和模型验证结果,对于Pitch轴,积分结构得到的传递函数拟合度比一阶惯性结构得到的传递函数拟合度稍高,所以选定积分结构所确定的传递函数;对于Yaw轴,一阶惯性结构符合实验数据,拟合度达到较高的95.6%。因此最终确定的Pitch轴和Yaw轴系统辨识环节传递函数分别为式(5)和式(6)。
3 控制器设计及仿真
根据建立的数学模型,已经辨识了从电流输入到角速度输出的传递函数,根据该环节的传递函数,对其建立起闭环控制可以有效增强角速度控制性能,增强该环节的抗干扰性,由此构建了一种串级双环控制系统。串级控制中副变量角速度的控制可以提高对主变量角度的控制质量,并减少进入副回路干扰对主变量的影响[8-9]。
在MATLAB的Simulink中建立增加校正环节的云台控制系统模型,经过参数整定,确定了Picth轴外环PID参数分别为Kp1=70,Kd1=30,Ki1=70,内环PID参数分别为Kp2=40,Kd2=40,Ki2=70。Yaw轴外环PID参数分别为Kp3=80,Kd3=20,Ki3=145,内环PID参数分别为Kp4=65,Kd4=28,Ki4=20。
两轴的仿真角度输出分别如图8和图9所示。
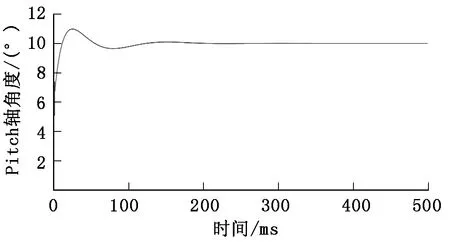
图8 Pitch轴串级PID仿真阶跃响应

图9 Yaw轴串级PID仿真阶跃响应
从图8和图9中可以看出:仿真中的Picth轴和Yaw轴控制系统的角度响应性能较好,过渡时间在100 ms左右。
4 云台控制实验
为了验证云台控制的平稳性和快速性,分别在遥控和定位控制下对其进行验证,并结合目标跟踪实验验证系统的稳定跟踪性能。
4.1 遥控
遥控即下位机处于遥控模式下,将遥控器通道值转换为需要控制的角度值,控制目标角度连续变化。图10和图11分别是两轴在遥控下目标角度曲线与实际角度曲线的对比。

图10 Pitch轴遥控目标角度与实际角度 图11 Yaw轴遥控目标角度与实际角度
由图10和图11可以看出:遥控模式下,目标角度变化平缓,Pitch轴和Yaw轴的实际角度都与目标角度基本重合。
4.2 定位控制
下位机处于定位模式下,由上位机向下位机发送一个较大的目标角度,实验结果如图12和图13所示。

图12 定位控制下Pitch轴实际角度与目标角度 图13 定位控制下Yaw轴实际角度与目标角度
在定位控制中,给定的是固定角度,从图12和图13可以看出:实际角度变化剧烈,存在小范围超调,稳态误差在±5%以内。
4.3 目标跟踪
在上位机利用机器视觉进行目标识别,获取对应目标的像素坐标之后,通过转换关系确定云台的目标角度,发送到下位机。
跟踪目标为色块物体,首先对图像进行颜色的RGB模型到HSV模型的转换,之后进行二值化处理,再进行直方图归一化和噪点处理,从而达到更好的区别效果[10-11]。图像处理之后进行轮廓检测,获取轮廓质心坐标,将像素坐标与质心中心坐标比较,再经过坐标转换输出目标值,并发送到下位机中。
基于目标识别和跟踪的原理进行实验,实验结果如图14和图15所示。

图14 Pitch轴目标跟踪角度曲线 图15 Yaw轴目标跟踪角度曲线
由图14和图15可以看出:在目标跟踪过程中,云台实际角度与目标角度能够较好地重合,对于相对角度不断变化的目标能够有效地进行稳定跟踪。
5 结束语
本文设计完成了一种具有俯仰角运动和偏航角运动的二自由度云台。基于系统辨识构建了系统模型,并设计了一种双环PID算法对控制系统进行校正,通过参数整定确定了参数。通过遥控实验、定位实验和目标跟踪实验完成了实际的实验验证,经过仿真后的控制算法能够较为有效地应用于实际设计的二自由度云台系统上,实现云台的稳定控制,达到了快速响应的目的。

