瓦房店市龙泉水库边坡稳定性评价
肖美艳
(瓦房店市水利勘测设计有限公司,辽宁 瓦房店 116300)
施工管理、工程设计和地质勘查的主要目标是准确评价工程边坡的稳定性,为此边坡稳定性问题逐渐成为国内外研究的重点课题[1]。例如,穆志江[2]对水利工程高陡边坡开挖稳定状况运用有限差分的FLAC软件实现了三维模拟分析,较为客观、准确的评判了工程边坡稳定程度;Zhou J W[3]对含软弱结构面的边坡稳定性运用SOSM二次二阶矩法模拟分析。然而这些方法大多以较为复杂的力学和数学原理为依据,其数值运算、参数模拟和建模分析过程较多,虽然其定量评价结果的可靠度较高,但评价分析边坡稳定性时的效率往往难以达到预期要求。水库工程初始建设阶段定性评价的适用性通常较定量分析更强。
近年来,计算机技术的快速发展对推动工程风险系统评估和边坡稳定性的定性分析发挥着巨大作用,尤其是人工智能和现代计算机技术的迅速发展,使得边坡稳定性研究越来越多的应用大量人工智能技术,如Hoang N D[4]采用先进的LSSVM最小二乘支持向量机、RBFNN径向基函数神经网络和ELM极限学习机等机器学习法,对比研究了边坡稳定性预测的实用性和有效性;Qi C[5]将耦合了ML算法和多元启发式的六种综合智能AI法进行了比较分析,提出对于斜率稳定性的预测集成的AI方法具有较大潜力;康飞[6]将机器学习理论与计算机试验相结合,提出了能够智能响应系统可靠度的框架体系;苏国韶[7]对边坡稳定性问题引入了高斯过程机器学习的定性方法。针对水库工程边坡稳定性的分析Logistic回归算法表现出较好适用性,通过设计配套的运算模型,可以快速输出能够反映水利工程边坡稳定性状态的评价结论。
1 Logistic回归模型
1.1 模型初步优化
对于可行性研究阶段的水利工程项目,可以将边坡稳定性问题判定为两种情况,即“稳定”和“欠稳定”,为了构成典型的离散变量预测问题将其利用“1”和“0”表征。因变量简明为该离散变量预测问题的典型特征,但水库工程边坡稳定性易受水文地质条件、岩层厚度、坡角、软弱结构面厚度与数量、底层岩性与地质年代、坡高等诸多因素影响,所以准确识别与边坡稳定性密切相关的因素为评价分析的重要环节。文章结合现有文献资料和水库工程实际情况,选取控制边坡稳定性的因子有年降水量、风化程度、岩体结构、坡角、地下水、软弱地层、底层岩性和坡角等,模型自变量为这些控制因子,采用Logistic回归模型揭示这些因子对边坡稳定性的作用机理。
1.2 水库边坡稳定性评价数学模型
1.2.1 评价模型的搭建
在选取自变量和因变量的基础上,运用数学语言将水库边坡稳定性评价模型表达为如下形式:
设y(i)(1≤i≤m)为模型因变量,其中m、i为参与评价的水库边坡总数和第i个边坡。根据以上分析结果y(i)符合条件,y(i)∈{0,1},y(i)=1、y(i)=0时判定水库边坡为“稳定”和“欠稳定”。
设xj(i)(1≤i≤m、1≤j≤n)为模型自变量,其中n为自变量维数,即识别的边坡稳定性评判因子个数,其他字母含义同上。
为了更好的描述因变量、自变量间的相互关系,引入z为中间变量,其数学含义为相应的权重值与各自变量值的乘积之和,表达式如公式(1)所示:
(1)
式中:θj为常系数,反映了边坡稳定性受各个因素的影响程度。
考虑到y(i)∈{0,1}的情况,可以选用概率值判断“1”与“0”,其物理意义是将因变量的取值概率选用合适的函数关系hθ(x)衡量,具体表达式如式(2)、式(3)所示:
(2)
(3)
式中:P(y=1|x)、P(y=0|x)——为稳定(y=1)和欠稳定“y=0”的概率,其中0 根据以上表达式,若z值较大且为正值,则P(y=1|x)=1、P(y=0|x)=0;若z值足够小且为负值,则P(y=1|x)=0、P(y=0|x)=1。因此,判别边坡是否稳定的条件可设定为适当的概率阈值。 1.2.2 模型的求解 求解未知量θ为Logistic回归模型运算的目标,对于θ的求解考虑选用最快梯度下降法。模型收敛性的判定为该求解过程的重要环节,对此可选取一个Cost函数作为目标函数,算法收敛状态的判定途径为Logistic回归中的Cost函数,其中算法求解达到收敛的判定标准为Cost函数达到最小值,即边坡稳定性区分的最优解为该条件下所获取的θ值。 采用Cost函数处理机器学习中的此类问题时,比较常见的表达式如式(4)所示: J(θ)= (4) 按照以下流程求解公式(5):为了获取最小的J(θ)值,对于样本已知的情况下若y(i)=1,为使得J(θ)减少应选用一个较大值替代式中的hθ(x(i));若y(i)=0,为使得J(θ)减少应选用一个较小值替代式中的hθ(x(i))。所以,通过判断边坡稳定性可以获取更优的一组θ值,一般选用最速梯度下降法作为θ的迭代方程,即如式(5)所示: (5) 式中:α为反映学习速率的常数,依据式(5)的运算途径可以实现Cost函数的最快下降,为了实现α的自动选取本文引入了系统软件自带的fminunc函数。 对于上述模型运用边坡稳定性已知的一系列数据完成学习训练,从而获取能够达到收敛时的Cost函数最佳θ值,然后利用公式(1)即可输出边坡稳定性判断的边界条件。 边坡稳定性评价模型按照以上思路求解时,定义年降水量、风化程度、岩体结构、坡角、地下水、软弱地层、地层岩性和坡高为模型自变量。其中,量化指标有年降水量、坡角和坡高,此类指标无需预处理,为了能够利用Logistic回归算法快速求解数学模型还需要量化处理其他自变量。根据工程建设相关资料和刘美芳等相关研究成果,提取复杂边坡管理系统中边坡稳定性量化指标,如表1。 表1 边坡稳定性量化指标 龙泉水库位于瓦房店市驼山乡曹屯村,即东经121°40′,北纬39°48′,是一座集防洪、灌溉于一体的小(2)型水库。该水库始建于1958年10月,坝址以上集雨面积3.47 km2,最大库容为17.97万m3。该水库可满足周边33.33 hm2旱田的灌溉,保护下游1个村2个自然屯460人。水库枢纽工程包括大坝、溢洪道、输水洞三大建筑物。 大坝:现坝顶高程40.35 m,坝长272 m,坝顶宽4.50 m,最大坝高5.99 m,大坝迎水坡比为1∶3.5,块石护坡,背水坡比为1∶2.0,草皮护坡。坝体防渗体为黏土心墙。 溢洪道:溢洪道位于大坝左侧,为正槽开敞式,底高程37.70 m,净宽10.00 m,边墙高1.24 m(衬砌2.00 m宽),末端无消能防冲措施。 输水洞:输水洞位于大坝的左侧,型式为坝下埋管,洞进口底高程35.20 m,洞径为Φ350 mm,输水洞现已报废并封堵。 根据龙泉水库地质调查相关资料和现场勘测有关数据,初步的定性判断库区边坡稳定性状态[8-13]。依据表1量化指标评判标准和工程地质调查资料,获取相应的量化值如表2。 表2 龙泉水库地质资料和数据量化 对相关数据的收集训练为Logistic回归建模的基本前提,因水库边坡为研究的对象,评价分析其稳定性状态为研究的内容,结合龙泉水库的评价指标和统计学大样本定义,借鉴相关文献资料获取边坡稳定性评价的30训练样本集。采用量化的形式衡量训练集有关数据,模型训练样本集量化数据如表3。 从表3可以看出,训练集中“稳定性”=1的正样本数有12个,“稳定性”=0的负样本数有18个,因此选取的水库工程正、负样本满足Logistic回归分析的均匀性分布要求。 2.2.1 Logistic回归的实现 根据表3可以看出,不同的水利工程样本其自变量取值存在较大的差异,如年降水量的数量级要高出岩性量化指标2个级别,Logistic回归在此条件下可能会出现无法获取最优解或收敛速度较慢的问题。所以,为解决以上问题应利用特征缩放每个自变量,其表达式如公式(6)所示: 表3 评价模型训练样本集量化值 (6) (7) (8) 其中,正则化项为与λ的乘积项,为有效防止过度拟合现象可选取合适的正则因子λ值。设λ=10,采用编制程序和以上公式经400次迭代运算后获取θ值。为了获取局部最优解θ,该条件下求解的Jmin(θ)=0.263 427,考虑到Cost函数的变化特征为凸型,则获取的θ值为全局最优。 结合全局最优解和以上转化处理搭建边坡稳定性预测模型,其数学表达式如式(9)、式(10)所示: z=θTx=-0.951 026+0.010 355x1+ 0.058 172x2-0.348 071x3-0.607 824x4- 0.035 677x5-0.374 50x6+0.002 852x7+ 0.001 672x8 (9) (10) 水库边坡稳定性评价模型和预测模型为公式(9)、公式(10),将以上公式输入待评样本的自变量完成预测评价;若hθ(x)≥0.5,则判定水库边坡为y(i)=1的稳定状态;若hθ(x)<0.5,则判定水库边坡为y(i)=0的欠稳定状态; 2.2.2 边坡稳定性评价 为进一步验证模型的科学有效性,将已构建的模型输入训练集中30个边坡稳定性已知的样本,运行模型完成稳定性判断。结果显示,模型预测结果与边坡稳定性真实判断基本相符,准确率达到95.48%,可见该模型符合边坡稳定性评价准确度要求[14]。 然后以瓦房店市龙泉水库工程为例,采用检验后的评价模型和已量化的已知自变量,最终输出为hθ(x)=0.563 551>0.5,按照相应的判别标准可认为该水库边坡处于“稳定”状态,水库边坡的稳定性较好可以满足工程建设要求,该评价结果与实际情况保持较高一致性。 文章结合Logistic回归思想搭建了能够定性反映边坡稳定性的评判模型。结合水库工程实际情况,选择控制坡体稳定性的坡角、坡高、地层岩性等8项典型因子,较为系统、全面的反映坡体的特征,可为评价模型的广泛应用提供重要支持。然后运用经过30个样本训练后的坡体稳定性评价模型,定性预测了瓦房店市龙泉水库的边坡稳定性,进一步验证了模型的实用性与可靠性。1.3 评价模型变量的参数化
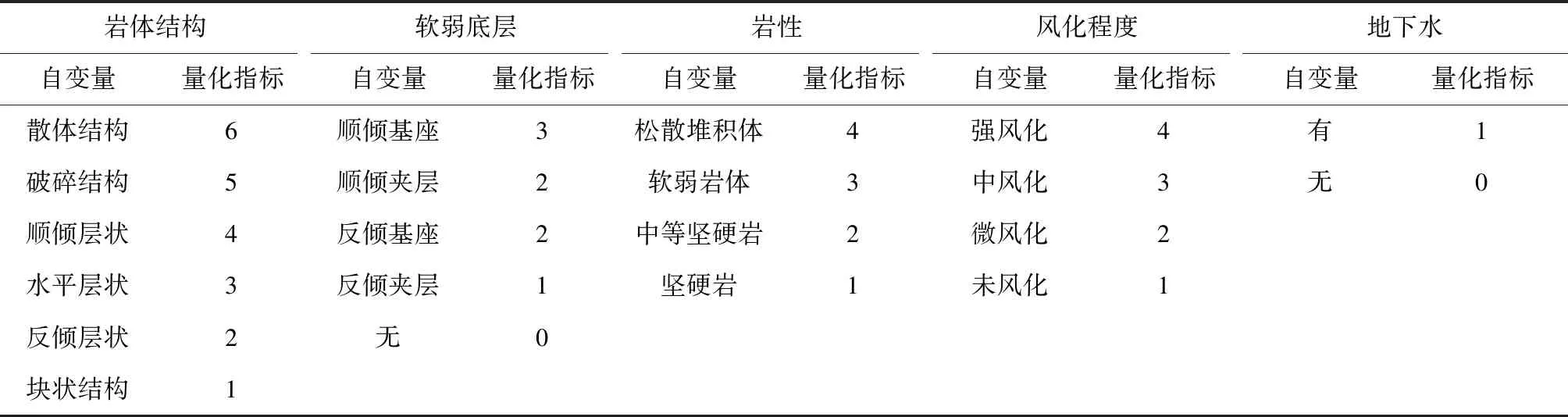
2 实例应用
2.1 训练集地质资料

2.2 Logistic回归及稳定性分析
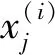
3 结 论

