非淹没双直立圆柱系统波浪爬升的数值模拟

陈浩民，倪云林

(浙江海洋大学 海洋工程装备学院，浙江 舟山 316022)

非淹没直立圆柱系统是近海构筑物和海洋平台常见的结构，当波浪在传播过程中遇到这些柱体时，就会产生反射、绕射和爬升。随着波浪沿柱体表面的迅速攀升，会对海洋构筑物产生撞击作用，从而影响其承载力和稳定性。关于波浪爬升问题，文献[1]基于线性势流理论，给出了规则波绕射单个直立圆柱的解析解；文献[2]通过物理模型试验，研究了大波陡波浪作用下直立圆柱的波浪爬升问题；文献[3]对规则波和随机波浪中的圆柱爬升问题进行了模型试验研究；Morris-Thomas[4]采用物理模型试验研究了波陡和散射参数对波浪爬升的影响。近年来，随着计算机技术的快速发展，基于三维数值水池的CFD方法被应用于波浪爬升问题的研究[5-6]。Morgan等[7]采用Open FOAM求解器，探讨了网格大小、离散格式、时间步长等因素对非线性波与圆柱相互作用的影响；武昕竹等[8-10]通过求解Navier-Stokes方程，结合VOF模型捕捉自由液面，计算了圆柱周围的波浪爬升效应；吴昊等[11]基于雷诺时均Navier-Stokes方程（RANS）和连续方程，结合k-湍流模型，建立了波浪与非淹没竖直圆柱相互作用的三维数值模型。

在研究波浪与海上建筑物相互作用时，缓坡方程凭借其精确的计算性和较小的计算量而被广泛应用。缓坡方程即联合折射绕射方程，最初由Berkhoff[12]基于线性波浪理论，在缓坡假定的基础上，采用小参数展开的方法推导得到。Booij[13]就该方程的适用条件，证明在地形坡度小于1∶3时，缓坡方程具有足够的精度。考虑到大部分近海构筑物或海洋平台由两个以上的直立圆柱构成，所以本文将采用有限元方法求解缓坡方程，研究波浪正向入射条件下，上、下游非淹没双直立圆柱周围的波浪爬升特性。

1 数值模型

1.1 控制方程

Berkhoff[12]推导的缓坡方程为：

式中：g为重力加速度。

当水深h为常数时，缓坡方程转化为Helmholtz方程：

图1 计算域划分示意Fig. 1 Division of computational domain

1.2 求解方法

本文采用Houston等[14-15]列出的有限元法求解缓坡方程。如图1所示，求解时将计算域分为水深变化的内域Ω1和水深恒定的外域Ω2，BI为内域中的物面边界，满足全反射条件，BC为外域和内域之间的公共边界，满足速度连续和速度势连续边界条件，B∞为无穷远边界，满足辐射边界条件。

外域不划分网格，利用Helmholtz方程的级数解析解和辐射边界条件，以Hankel函数Gi(i=1, 2, ···, M,M为截断项)作为权函数，通过格林公式将外域面积分转为边界上的线积分，建立单元有限元方程：

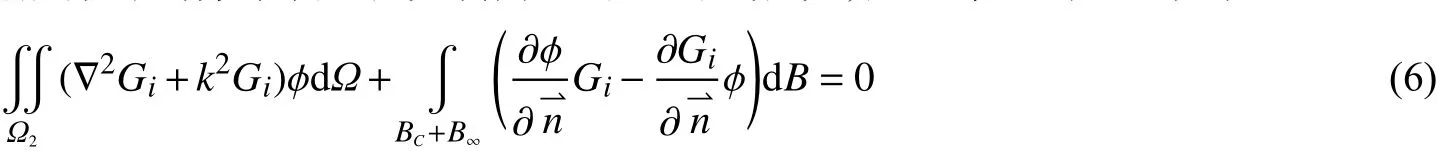
各单元有限元方程经总装形成总矩阵方程组后可采用列主元高斯消去法求解。

1.3 模型验证

为了验证本文数值模型的正确与否，首先计算非淹没单个直立圆柱周围的波高分布。如图2所示，圆柱直径d=0.522 m，淹没深度h=0.165 m；波浪沿x轴正方向入射，波高H0=0.079 m，周期T=0.94 s，波长L=1.046 m。图2中圆环部分为内域，大小为用Gambit软件划分网格。在兼顾计算精度和计算速率的前提下，1个波长范围内设置15个三角形六节点网格，内域总计9 098个单元，18 444个节点。

计算结果绘于图3。可以看出，本文的数值解波浪爬高Hi与文献[1]提出的线性解析解吻合很好，最大波高位于圆柱迎浪点（θ=0°）位置处，其值约为入射波高的1.8倍，最小波高位于圆柱背浪点（θ=180°）左右两侧35°位置处，即θ=145°，其值约为入射波高的50%。这证明了本文数值模型的正确性，其计算结果准确可靠。

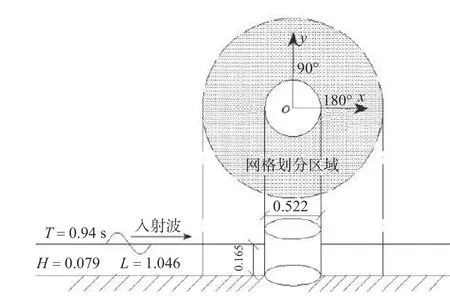
图2 非淹没单个直立圆柱地形（单位：m）Fig. 2 Sketch of single non-submerged vertical circular cylinder (unit: m)

图3 单个直立圆柱周围波高分布比较Fig. 3 Comparison of calculated wave run-up with analytical solutions along circumference

2 非淹没双直立圆柱系统波浪爬高的数值模拟

为了进一步研究非淹没双直立圆柱系统中圆柱间距对波浪爬升的影响，如图4所示，在沿波浪传播方向上布置两个直立圆柱，分别将其命名为上游圆柱和下游圆柱，圆柱尺寸和波浪要素与上文模型验证中的算例参数相同，两圆柱间距为S。针对不同的工况，S是唯一变量，其变化范围是1 . 25L≤S≤3.00L，变化步长为0.25L，计算工况1～8对应的圆柱间距分别为1.25L、1.50L、1.75L、2.00L、2.25L、2.50L、2.75L和3.00L。

图4 非淹没双直立圆柱地形（单位：m）Fig. 4 Sketch of dual non-submerged vertical circular cylinder(unit: m)

2.1 上游圆柱波浪爬升特性

不同间距条件下，上游圆柱周围波高分布随圆柱间距 S 的变化情况及其与单个直立圆柱的对比见图5。

相较于单个圆柱的情况，波高分布曲线存在较大的波动现象，具体表现为：

（1）当圆柱间距为1/4波长的整数倍时，即 S /L=n/4(n=5,6,···,12)时，最大波高的出现位置和最大波高值与单个圆柱的情况基本相同，均位于圆柱迎浪点（θ=0°）处，最大值约为入射波高的1.8倍。

图5 圆柱间距改变对上游圆柱波浪爬高的影响Fig. 5 Influence of spacing between two cylinders on wave run-up of upstream cylinder

2.2 下游圆柱波浪爬升特性

图6 是下游圆柱周围波高分布随圆柱间距S的变化情况及其与单个直立圆柱的对比。可以看出，在不同圆柱间距的工况下，下游圆柱周围的波高分布曲线与单个直立圆柱的情况相似，最大波高均位于圆柱迎浪点（θ=0°），最小波高均位于圆柱背浪点左右两侧 35°处（θ≈145°），最大值和最小值计算结果详见表1。

分析表1可见：

（1）受上游圆柱的掩护作用，下游圆柱周围相对波高的最大值和最小值均小于单个圆柱的情况。

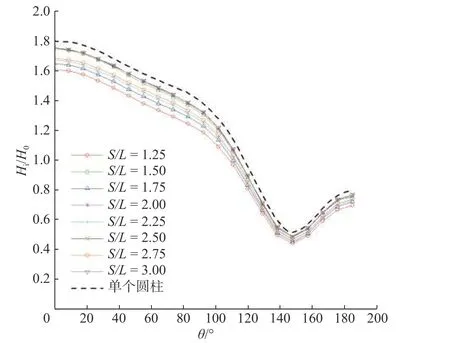
图6 圆柱间距改变对下游圆柱波浪爬升的影响Fig. 6 Influence of spacing between two cylinders on wave run-up of downstream cylinder

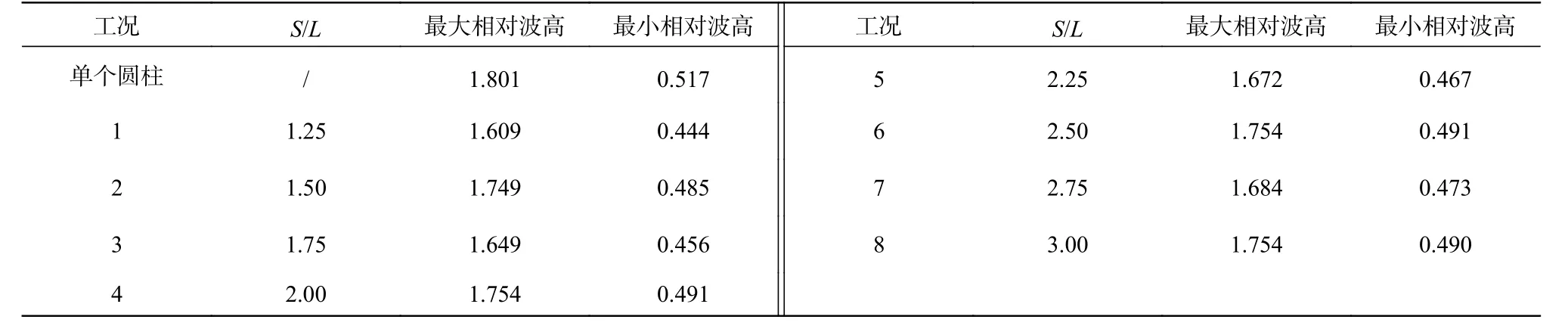
表1 下游圆柱波浪爬高最大值和最小值Tab. 1 The maximum and minimum values of wave run-up around downstream cylinder

3 结 语

（1）本文采用有限元方法建立了缓坡方程数值模型，利用该模型计算了非淹没单个直立圆柱周围的波高分布，计算结果与解析解吻合很好，证明了本文数值模型的正确性以及用其求解圆柱周围波浪爬升问题的适用性。

（2）相较于单个圆柱，上游圆柱周围波高分布曲线的波动较大，但它们的最大相对波高和最小相对波高发生位置基本一致。同时，当圆柱间距为1/4波长的奇数倍时，即 S /L=(2n+1)/4(n=2,3,4,5)，最小相对波高明显小于单个圆柱的波高，并在圆柱肩部出现第二峰值；而当圆柱间距为1/4波长的偶数倍时，即S/L=2n/4(n=3,4,5,6)，最小相对波高则明显大于单个圆柱的波高，并在圆柱肩部出现第二谷值。这是由上游圆柱的绕射和下游圆柱的反射所引起。

（3）下游圆柱周围的波高分布曲线与单个圆柱的情况相似，但受上游圆柱的掩护作用，其最大相对波高和最小相对波高均小于单个圆柱的情况。

（4）吴昊等[11]基于黏性流理论，研究了非淹没双直立圆柱系统的波浪爬高问题，结果表明，当圆柱间距较大时，下游圆柱壅水效果降低，波浪爬升减弱；当圆柱间距较小时，圆柱之间壅水效果增强，上游圆柱背浪面的波浪爬高逐渐上升。上述结论与本文采用势流理论得到的结果基本一致。