三参数下BS疲劳寿命分布的统计分析①
何友谊
(湖南文理学院师范学院,湖南 常德 415000)
0 引 言
电子产品性能的退化、设备材料零件的损坏、人体器官结构的病变等问题大都并不是由外力瞬间造成,而是因来自自身或外界的某些因素长期的干扰造成的,想要研究这些因素的影响就需要建立起合适的模型。1969年,Birnbaum 与 Saunders 在研究周期应力之下由于疲劳度逐渐累积、裂口进一步扩展而导致失效的机器零件的模型时,提出了这种描述产品寿命的新分布,Birnbaum-Saunders疲劳寿命分布[1]从此应运而生。相比Weibull分布、对数正态分布等这类通常适用于描述产品寿命的分布,由于其疲劳失效的基本特征,那些因疲劳导致失效的产品寿命特征用BS分布来表述更贴近。因此,无论是可靠性统计分析中的疲劳失效研究,还是性能退化评定,该分布模型都运用广泛。又因为该分布的参数估计相对难度较大,有必要探究简便而适用的估计方法,并对其进行更进一步的分析改进与研究,无论在理论研究还是实际应用上都将是意义重大的。
1 预备知识
Birnbaum-Saunders 疲劳寿命分布(以下将简称BS分布)的分布函数为
此处,V~N(0,1),α>0为形状参数,β>0为刻度参数,同时记T~BS(α,β).
BS分布的概率密度函数为:
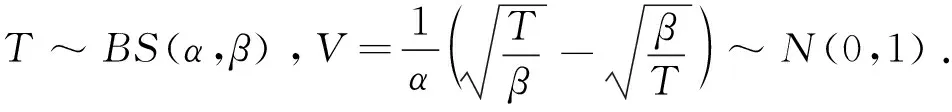
BS分布的分布函数F(t)和概率密度函数f(t)另可表示为
α,β同上,Φ(x)为标准正态分布N(0,1)的分布函数,φ(x)为密度函数,即
对于BS分布的相关问题,国内外已有不少文献对其参数估计进行了研究分析[1-3,6-10]。从上面可以看到,该分布的密度函数相对复杂,这样也对其参数的估计问题造成了一定的难度。因此,不少文献从估计方法上进行了不断地研究改进,同时,在 BS 分布模型上,不少文献也做了一些新的改进,提出了新的寿命分布族如广义BS分布等等。
比较典型的,如Leiva等基于广义 BS 分布族的探讨提出新的寿命分析,并运用迭代思想得到参数的MLE与其他推断,进一步进行优度拟合使得数据估计更优异[11];Owen通过放宽独立性假设分别提出全新的两种广义三参数 BS分布[12,13],裂缝的扩展被重新定义建模,使得这种具有两个形状参数的分布成为了一个灵活性很强的分布。
2 参数估计及主要结果
基于两参数BS 寿命分布,通过增加参数对其进行推广,设T服从三参数BS寿命分布T~BS(μ,α,β),令其分布函数为:
密度函数为:
其中,μ>0为位置参数,α,β,Φ(x),φ(x)同上。
由于
令
则
联系矩估计的思想方法,构建并形成方程组:
若直接求解该方程组,由于其结构相对复杂,造成不便与困难。
于是,令U=T-1,对u>0
FU(u)=P(T-1≤u)=
即T-1~BS(α,β-1).
于是,可以建立如下矩方程组:
于是有
故得关于位置参数μ的超越方程:
即有
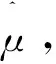
3 结 语
基于两个参数的Birnbaum-Saunders分布,通过位置参数μ的增加,新定义了含有三个参数的BS寿命分布,由于其分布结构的复杂性,采用矩估计思想对参数进行了研究分析,丰富了BS分布的相关理论。当然,文中的统计研究还有一些仍需要不断完善和进一步探讨的地方,比如平均剩余寿命分布还未探讨,对矩估计也可进行一些随机模拟,进而确定其精确性方便与其他估计作比较,也可以适当研究参数的其他估计方法如区间估计等等,这都是今后可以继续进一步研究的方向。

