基于改进粒子群优化算法的太阳能发电系统无功优化

李旭炯，孙林花

（兰州资源环境职业技术学院，甘肃 兰州 730021）

0 引 言

近年来，太阳能（Photovoltaic Power，PV）发电无论从建设规模和入网数量都发展迅速。通常，太阳能从配电网侧接入主网，导致配网结构由单源放射状变为多源放射状结构，原有单向潮流分布和负荷分布也会改变，造成无功功率不稳定，配网运行和控制更加复杂[1]。因此，配网无功功率优化是提高系统稳定性的有效措施。

本文以系统的有功功率为对应函数，考虑有功、无功以及电压的约束，建模太阳能发电接入配网时无功功率优化模型，提出改进粒子群算法（Improved Particle Swarm Optimization，IPSO），在迭代中惯性权系数线性减小。最后依托IEEE 33系统仿真分析，验证其可行性。

1 带太阳能发电的配网无功优化模型

1.1 目标函数

从配网经济运行的角度出发，对应函数设定为使有功损耗达到最小：

1.2 约束条件

平等约束条件为：

式中，Pi、Qi、Vi分别代表有功功率、无功功率、节点i的电压，Gij、Bij、δij分别代表电导、电纳、节点间的相位角差。

不等式约束条件为：

式中，Vi为节点i电压幅值，Vimin、Vimax为节点i电压幅值的上下限，Qi为太阳能发电系统无功输出，QGimax、QGimin为太阳能发电系统无功输出的上下限，Qimax、Qimin为系统无功补偿设备容量的最大、最小值。

2 惯性权系数线性动态变化的PSO

2.1 IPSO

IPSO是对简化社会模型的仿真而发展起来的。该算法特点如下[2]：

（1）基于鱼群和鸟群这些群体性动物的研究；

（2）计算时间短，所需存储量少。

IPSO搜索过程可描述为：一群粒子优化某一个特定的目标函数，且每个粒子都知道各自的最佳值（体极值）和坐标，此外每个粒子也知道其在组群中的最佳值（全局极值），也就是组中目前为止的最优值。利用当前速度及与体极值与全局极值的距离，可以得出每个粒子的修正速度，表示为：

式中，为迭代k时粒子i的速度，为粒子i的修正速度；rand为0～1的随机数，为迭代k时粒子i的当前位置，pbesti为粒子i的体极值，gbesti为粒子i的全局极值，wi为粒子i的速度权函数，ci为每一项的权重系数。

本文在迭代过程中采用惯性权系数w由0.9线性减小到0.4的措施，式（5）中函数的系数w设为如下方程：

式中，wmax=0.9，wmax=0.4，itermax为最大迭代数，iter为当前迭代次数。

搜索过程中，惯性权重因子呈线性递减的趋势，开始时，w最大，对应的整体搜索能力也表现最强，能够很快地定位最优解。迭代后期，w逐渐减小，对应的部分搜索能力得到了提高，可准确地确定最优解的位置[3]。

2.2 程序设计及算法流程图

IPSO的实现步骤如下：

第一步，利用初始化参数（种群数量、粒子数目、迭代次数以及惯性权重因子），随机生成粒子的初始搜索点和速度；

第二步，每个粒子搜索点损耗由潮流计算得到，如违反约束，在损失基础上增加惩罚；

第三步，将体极值设为每个初始搜索点。将体极值中的初始最优评估值（损失加惩罚）设为全局极值；

第四步，计算新速度，连续变量采用连续方程，离散变量采用离散方程；

第五步，计算新搜索点，连续变量采用连续方程，离散变量采用离散方程；

第六步，计算新搜索点和估计值的损耗；

第七步，如果每个粒子的估算值优于之前的值，则将这个值设为体极值，如果最优体极值优于全局极值，将此值设为全局极值，存储所有全局极值作为最终控制策略的候选值；

第八步，如果迭代数达到最大值则修正，否则回到第四步。

结合潮流计算，整个潮流优化程序流程如图1所示。

图1 算法流程图

3 实例分析

为验证所提算法可行性，依托融合太阳能发电系统的IEEE 33节点系统，通过如下的3种方案仿真分析，并进行了比较。

方案1，电流系统中不存在用于无功补偿的设备，太阳能发电系统的无功调节也忽略不计，结构如图2所示。

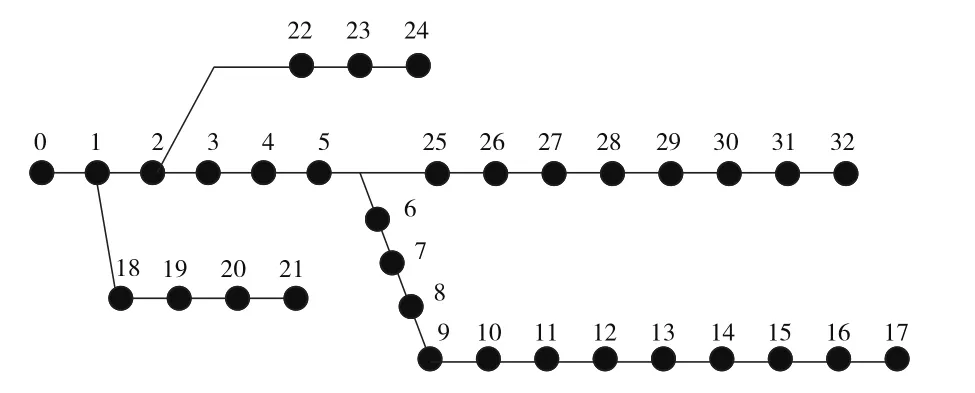
图2 IEEE 33节点系统

方案2，不管太阳能发电系统的无功调节能力有多强，只通过无功补偿装置来调节无功。因为并联电容器安装节点越靠近线路末端，配电网损耗越小，网损优化效果也越好。因此，选取第24号和32号节点作为并联电容器组的接入点，每组电容器为50 kvar，可补偿配电网中的无功功率。表1为方案2接入节点及并网设备参数表。

表1 方案2接入节点及并网设备参数表

方案3，同时接入无功补偿装置和太阳能发电系统，系统无功功率由太阳能发电系统和无功补偿装置调节。太阳能发电系统输出有功功率为Pact=400 kW，无功功率输出的最大值为|Qmax|=184 kvar，假设节点10和17为太阳能发电系统的接入点。表2为方案3接入节点及并网设备参数表。

表2 方案3接入节点及并网设备参数表

通过Matlab仿真，得到3种方案的损耗和最小电压。3种方案的节点电压对比如图3所示。

图3 3种方案的节点电压对比

可以看出，方案3既包含无功补偿装置，又融合了太阳能发电系统的无功功率，优化结果最好，节点电压支持能力最强，系统有功损耗最小。已知每个电容器组容量值是50 kvar，因此方案2中，两个无功设备的电容组数为11和16，而方案3中，两个无功设备的电容组数为10和12。适当增加太阳能发电设备可降低无功设备的投资，节约运行成本。

4 结 论

本文通过太阳能发电系统本身的无功功率调节能力，针对每个节点约束，建立了太阳能并网配电网无功优化模型。通过引入动态惯性权值因子改进传统PSO，解决以往算法不能将整体和部分搜索能力一同兼顾的问题，通过计算机仿真分析，获得了优化结果。结果表明，太阳能发电并网接入配网，可减少无功补偿设备的投入，节约运行成本。通过基于IPSO的无功功率优化，可有效降低系统的损耗，提高系统运行的稳定性和适应性，实验结果说明了该算法在优化系统无功中的有效性。