将数学建模思想引入“贝叶斯公式”教学中的案例实施

曹建美，冯晨娇，王凤翔

（山西财经大学应用数学学院，山西太原030006）

0 引言

“概率论与数理统计”是研究随机现象统计规律性的一门学科，因其抽象性强、题型灵活，需要扎实的“高等数学”基础，被大多数学生认为是大学本科阶段3门公共数学课程中最难学习的一门课程。数学建模是将实际问题抽象转为数学问题，使用数学公式、图形等进行推导演绎进而来研究实际问题的一种思想和方法［1］。将数学建模思想引入“概率论与数理统计”课程的教学改革，旨在增强大学生熟练运用数学知识解决实际问题的能力，培养学生的学习兴趣，并进一步培养学生的创新能力。概括起来，教师可在新课导入、知识应用、课后拓展3个教学环节中结合数学建模进行案例教学［2-3］。本文选用“贝叶斯公式”一节，探讨如何实施将数学建模思想引入“概率论与数理统计”课程的案例教学。

1 贝叶斯公式及全概率公式的推广概述

1.1 贝叶斯公式与证明

设B1，B2，…，Bn为Ω的一个分割，即B1，B2，…，Bn互不相容，且B i=Ω，如果P（A）＞0，P（Bi）=0（i=1，2，…，n），则P(B i A)=,i=1,2,…,n。

证明：由条件概率的定义（所谓条件概率，是指在某事件B发生的条件下，求另一事件A的概率，记为P(A B)）

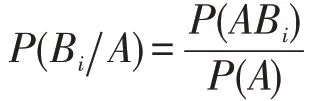
对上式的分子用乘法公式、分母用全概率公式，P(ABi)=P(B i)P(A Bi)

P(A)=P(B i)P(A Bi)

P(B i A)=,i=1,2,…,n

结论得证。

1.2 贝叶斯公式及其与全概率公式的联系

介绍了贝叶斯公式后还需介绍全概率公式，因为全概率公式和贝叶斯公式是一组互逆公式。以下先了解全概率公式的概念。

设B1，B2，…，Bn为样本空间Ω的一个分割，即B1，B2，…，Bn互不相容，且Bi=Ω，如果P（Bi）＞0（i=1，2，…，n），则对任一事件A有P(A)=P(B i)P(A|B i)

证明：因为

A=AΩ=A

且AB1，AB2，…，ABn互不相容，所以由可加性得

P(A)=P

再将P(AB i)=P(B i)P(A|B i),i=1,2,…,n代入上式即得：

由证明可知，全概率公式就是贝叶斯公式的一种变形，它与贝叶斯公式是互逆应用的，与贝叶斯公式一样在实际生活中也有很广泛的应用。以下来探讨贝叶斯公式在几个方面的应用。

1.3 贝叶斯公式推广与证明

1.3.1 贝叶斯公式的推广

设当试验的随机过程不少于两个的时候，在影响目标事件的每一个试验过程中分别建立完备事件组，贝叶斯公式即可进一步推广。

1.3.2 贝叶斯公式推广定理

设Ai（i=1，2，…，n）和Bj（j=1，2，…，n）是先后两个试验过程中的划分，C为目标事件。当P（C）＞0，P（Ai）＞0，P（Bi）＞0，P（AiBj）＞0，i=1，2，…，n，j=1，2，…，m时，则有：

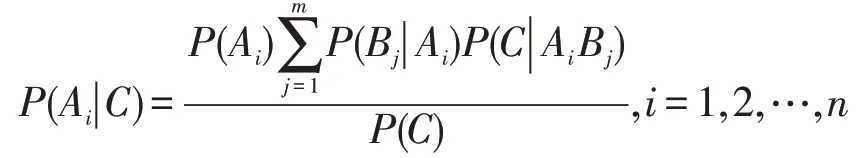
P(B j|C)=,j=1,2,…,m

P(A i B j|C)=,i=1,2,…,n,j=1,2,…,m

证明：（1）P(Ai|C)==

同理可以证明（2）、（3）。

1.4 贝叶斯公式推广总结

整理文献后，可把贝叶斯公式归为两种形式，即事件型和随机变量型，这是就样本本身的性质而言的。上述推广结论是由不同的技巧推广而来的。从公式的条件出发，讨论拓宽公式应用的面。在经典的贝叶斯公式当中要求事件列是“互不相容”的，这方面削弱了这一条件给出广义的贝叶斯公式，无论相容与否都可以直接计算。从公式的形式出发，增加公式的灵活度。例如：在经典的贝叶斯公式中，样本是离散的，但是实际计算当中，遇到复杂事件的时候，就不太实用了，这时候可以把全概率公式推广到随机变量的情形。当然，随机变量有可能是离散的，或者是连续的，也可能是混合型随机变量，所以可以再利用分布律来求解有关问题。从公式的计算辅助出发，创新地利用公式的推广，用在风险模型的改进、风险计算和风险过程的分析当中。但是可以发现，随机变量的贝叶斯公式的推广结论，要明显少于事件型的推广结论。一方面，随机过程是一门很深很难的学科；另一方面，贝叶斯公式还是局限在概率的计算这个问题中，用于例子的一般计算，采用事件型就能够完成。然而，随着各个学科的相互渗透，事件型概率虽然已有较多的推广形式值得学习和借鉴，但是当遇到实际问题时，还是要对贝叶斯公式形式作一些新的变化，使之能更好地为计算和研究服务。

2 在“新课导入”环节结合数学建模思想和方法，通过案例教学导入新知

例1.由包括中国学者在内的新冠病毒（COVID-19）紧急系统性综述工作组完成的一项研究在《柳叶刀》杂志发表［4］，该研究科学论证了保持1 m以上社交距离、戴口罩和眼睛防护是预防新冠病毒感染的有效手段。其中，戴口罩这样一项在中国司空见惯的预防措施，在欧美国家却成了较难实行的一项措施。试用概率知识解释戴口罩的必要性。

分析（实际问题数学化）：在一个高风险地区，假设该地区的居民能够保持安全的社交距离与眼部防护，如果已知一个人感染了新冠肺炎，求他是因为没戴口罩被感染的概率。

之后，需要“设事件”，设B表示“居民感染新冠”，A1表示“居民佩戴口罩”，A2表示“居民不佩戴口罩”，则该数学问题是求P（A2|B）。

解：首先，对该问题进行一些合理的假设。

2.1 模型假设

①假设在一个偏好戴口罩的地区，有95%的人习惯戴口罩，5%的人不习惯戴口罩；

②假设在一个不偏好戴口罩的地区，有5%的人习惯戴口罩，95%的人不习惯戴口罩；

③假设在高风险地区，佩戴口罩时被感染的概率为3.1%，不戴口罩时被感染的概率为17.4%［4］。

2.2 模型建立

根据条件概率公式，P（A2|B）=P（A2B）/P（B）。对于分子，根据乘法公式，可知P（A2B）=P（A2）P（B|A2），对于分母，要求P（B）。从题中可以看出，排除其他情况，有两个情况可能会出现“居民感染新冠”这个结果，分别是情况1——居民佩戴口罩（A1），或情况2——居民未佩戴口罩（A2）。因此，“居民感染新冠”可包括两种情况：居民佩戴着口罩同时被感染，或者居民未佩戴口罩同时被感染，即B=A1B+A2B，从而P（B）=P（A1B+A2B）。由于A1B与A2B不同时发生，故P（B）=P（A1B）+P（A2B）。使用乘法公式，P（A1B）=P（A1）P（B|A1），P（A2B）=P（A2）P（B|A2），得到P（B）=P（A1）P（B|A1）+P（A2）P（B|A2），这就是已经学习过的全概率公式。将分子、分母分别代入，可得到P（A2|B）=P（A2）P（B|A2）/［P（A1）P（B|A1）+P（A2）P（B|A2）］，即可推导得出贝叶斯公式。

2.3 模型计算

如果是在不偏好佩戴口罩的地区，由假设，P（A1）=5%，P（A2）=95%，P（B|A1）=3.1%，P（B|A2）=17.4%，该概率为：

P(A2|B)=

为了便于学生比较，可引导学生自行计算“如果已知一个人感染了新冠肺炎，求他是戴口罩情况下被感染的概率”，即计算P（A1|B）。在一个偏好戴口罩的地区，由假设，P（A1）=95%，P（A2）=5%，P（B|A1）=3.1%，P（B|A2）=17.4%，该概率为：

P(A1|B)=

（4）模型应用。

通过计算发现，如果一个居民不幸感染了新冠，在不偏好戴口罩的地区，他是在没戴口罩情况下被感染的概率高达99.1%，而在偏好戴口罩的地区，这一概率约为22.8%。这个结果充分验证了西方国家和中国在预防新冠肺炎时面临的防疫形势，结果令人信服，同时从概率论的角度解释了戴口罩进行防疫的必要性。

在求解的过程中用到了一个公式：P(A2|B)=，即概率论中非常重要的贝叶斯公式。教师可继续引导学生总结贝叶斯公式的使用条件、适用题型（执果索因）、推广形式（可推广到n个原因）。

在解决实际问题的同时，通过数学建模思想，由浅入深，循序渐进地推导出本次课程的主题内容——贝叶斯公式，学生感觉公式的给出合情合理，避免了直接讲解公式时学生感觉知识点的学习如无本之木、无源之水的困境。

3 在“知识应用”环节利用数学建模思想和方法进行案例教学达到知识巩固

例2.利用概率知识解释“狼来了”的寓言故事中村民对放羊娃的信任度是如何下降的。

解：（1）模型假设。

①假设一个孩子是诚实的孩子的概率为0.8；②假设一个诚实的孩子会说谎的概率为0.1；③假设一个不诚实的孩子会说谎的概率为0.5。

（2）模型建立。

用A1表示“孩子是诚实的”，A2表示“孩子是不诚实的”，B表示“孩子说谎”，根据贝叶斯公式：

P(A1|B)=

（3）模型计算。

由假设可知，P（A1）=0.8，P（A2）=0.2，P（B|A1）=0.1，P（B|A2）=0.5，则放羊娃第一次说谎后，村民对其信任度为：P(A1|B)==0.444

在放羊娃第一次说谎后，在村民眼中，这个孩子是诚实的概率降为0.444，即此时可认为P（A1）=0.444，P（A2）=0.556。继续计算，放羊娃第二次说谎后，村民们对放羊娃的信任度：

P(A1|B)=≈0.138

（4）模型应用。

放羊娃两次说谎后，村民们对放羊娃的信任度从最初的0.8下降为0.138，所以这个故事的结局是悲惨的，放羊娃因为自己的一再说谎付出了生命的代价。本例是贝叶斯公式的一个应用案例，通过对“狼来了”这一寓言故事进行数学建模分析，既让学生深刻理解了该寓言故事蕴含的“诚信做人”的深刻内涵，同时还能帮助学生掌握贝叶斯公式的使用条件、适用题型，并培养学生利用所学数学知识解决实际问题的能力，极大地激发了学习兴趣。

4 在“课后拓展”环节结合数学建模思想和方法来进行案例教学达到知识拓展

例3.垃圾邮件的识别、智能手机自动翻译、语音识别等很多人工智能现象的关键算法核心都是贝叶斯公式。请各小组结合数学建模的思想和方法探讨贝叶斯公式是如何应用到这些实际问题中建模的，并提交小组报告一份。

这是一个开放性的课后拓展作业，学生在课后可以查阅资料，小组讨论，团队协作，结合数学建模的思想和方法完成一篇研究报告。限于篇幅，这里不再赘述。

5 结语

贝叶斯公式在很多数学模型中有很重要的作用。对贝叶斯公式进行仔细分析，用例子说明了它的用法及所适用的概型，为了解决实际问题的需要，将贝叶斯公式进行了推广，用例子说明了推广的贝叶斯公式在实际应用中所适用的概型比贝叶斯公式的更广。因此，贝叶斯公式在数学模型的求解中有着十分广泛的作用，它是数学模型中一个经常会被用到的工具。社会在飞速发展，决策者必须综合考察以往的信息及现状从而做出综合判断，决策概率分析越来越显示其重要性，其中，贝叶斯公式主要用于处理先验概率与后验概率，是进行决策的重要工具。

教师在课堂教学各个环节中有意识地融入数学建模的思想和方法进行案例教学，将“概率论与数理统计”的理论知识与实际问题结合起来，可以达到3个方面的教学效果：第一，让学生充分认识到该课程的实际应用，使得课程学习从“无用”变得“有用”；第二，让学生逐步了解了数学建模的本质，掌握了数学建模的基本方法，培养了学生解决实际问题的能力和创新能力，激发了学习兴趣，使得课程学习从“无趣”变得“有趣”；最后，学生对课程知识的理解得到深化，提高了学习效率，使得课程学习从“困难”变得“不难”。随着教学活动的不断深入，如何更加有效地融入数学建模的思想和方法，不断提高教学质量，这是需要进一步探讨和完善的地方。