基于上限定理的浅埋巷道掌子面稳定性分析

王国科

(浙江佳途勘测设计有限公司,浙江 丽水 323000)

巷道开挖后,岩土原有的应力平衡被破坏,应力重新调整,掌子面形成应力集中,极易形成垮塌破坏,进而造成重大损失.因此,确定围岩压力成为掌子面稳定性分析中的关键问题,研究巷道掌子面的稳定性问题具有重要的理论价值和工程意义.

在岩土工程领域中,极限分析理论具有计算过程简单、快捷,计算结果较准确的优点[1],所以,近几年在分析隧道稳定性问题中运用较广泛,基于非线性准则和极限分析法求解围岩压力已经被国内外许多学者采用[1].Daniel等[2]采用刚性块上限法和有限元极限分析法研究了方形巷道在不排水黏土中的稳定性,但是方形巷道在工程应用中并不多见,不太具有实际意义;Kentaro等[3]研究了在荷载作用下黏性土中双圆弧巷道的稳定性问题,将双圆弧巷道的中心距作为一个新的问题参数,采用有限元极限分析技术得到了最终的附加荷载，但是其模式构建方法比较复杂,不便于在实际工程中进行推广和应用;Huang等[4]研究了不排水黏性土不排水隧洞的稳定性,用多刚体块上限法得到了围岩压力的上限解析解,并对浅埋巷道平面应变稳定问题进行了较为准确的预测,但假定剪切强度随深度呈线性增加不太符合实际;Salvador等[5]基于极限分析法构建了隧道的旋转面垮塌机制,预测了临界压力和垮塌的类型;Nima等[6]将土体黏聚力的线性变化与深度的极限分析的上限定理应用于封闭面开挖巷道掌子面的压力计算,采用强度折减法和上限定理计算了巷道掌子面失稳的安全系数,分析采用平均土壤凝聚力和局部凝聚力会在施工中带来的不良后果,但并未给出适合的土壤凝聚力的取值范围;杨小礼等[7]根据极限分析上限定理,推导了圆形浅埋巷道围岩压力的计算公式,并计算出了围岩压力的最优解,但其使用的圆形巷道破坏模式不太适用于实际工程中;Davis等[8]假定了4种不同的破坏模式,根据极限分析法上限定理对黏性土在不排水条件下的浅埋巷道的围岩稳定性进行了分析;张佳华等[9]根据虚功率原理,从能量的角度出发,对浅埋偏压巷道的稳定性系数和支护力进行求解,并且对计算结果进行对比与分析,但其计算的精度有待提高;杨子汉等[10]通过构建二维多块体滑移破坏模式,采用极限分析法得到了不同饱和度下计算巷道掌子面破坏范围的公式，该多块体破坏模式并不是真正意义上的破坏模式,还需要做进一步的改进.

上述研究运用极限分析上限定理研究巷道稳定性问题,并且分别采用的是Mohr-Coulomb破坏准则或Hoek-Brown破坏准则.但是Mohr-Coulomb破坏准则和Hoek-Brown破坏准则都有一定的局限性,Mohr-Coulomb破坏准则更适合土体,Hoek-Brown破坏准则更适合于岩体.而非线性Baker破坏准则包括了这两种破坏准则,适用范围也更加广泛.为了扩大适用范围,本文采用非线性Baker破坏准则,运用极限分析上限法研究巷道开挖掌子面的稳定性.

1 非线性Baker破坏准则及其切线技术

Baker[11,12]基于三轴试验和已有试验研究结果,提出了一种广义的岩石强度准则.Baker提出的非线性强度准则如式(1).

(1)

式中:τ表示剪切应力；Pa表示大气压强；σn表示法向应力；A,n和T为相关参数.

通过切线技术[15],将非线性Baker强度准则式(1)写成Mohr-Coulomb强度准则的形式,式(1)通过固定点(0,PaATn)和(-PaT,0)两点.将式(1)绘制成曲线,见图1.

图1 非线性Baker破坏准则表示的强度曲线

对于强度包络线上的任意一点M,其对应的Mohr-Coulomb强度准则的表达式为

τ=ct+tanφt·σn.

(2)

式中:ct和φt分别为M点处的黏聚力和内摩擦角,可由式(3)和(4)确定.

(3)

(4)

其中式(4)即为Baker强度准则下几个非线性参数的关系式.

2 极限分析上限定理

极限分析法以一种理想的方式考虑了岩土体的应力应变关系.上限定理要求对于任意机动容许的破坏机制,内能损耗率不小于外力功率,可用式(5)表示.

(5)

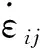
3 破坏模式的构建

许敬叔等[16]采用的对数双螺旋破坏模式已被证明适用于浅埋巷道掌子面的稳定性研究.本文基于对数双螺旋破坏模式构建的掌子面前方土体的主动破坏模式，如图 2所示.破坏范围由两条对数螺旋线HE和BE组成,ra,rb分别表示OH,OB的长度.O为HE和BE的旋转中心.两条对数螺旋线绕旋转中心O点以恒定的角速度ω转动.两条对数螺旋线相交于E点,在E点形成一个大小为2φt的夹角.OH,OB,OE与竖直方向的夹角分别为θ1,θ2,θ3.C表示巷道的深度,D表示巷道的宽度.HB为巷道的掌子面.开挖过程中,掌子面的支护荷载视为均布荷载,用σ0表示.

图2 浅埋巷道掌子面破坏模式

其中:对数螺旋线HE和BE的表达式如式(6)和式(7)所示.

r1=raexp[(θ1-θ)tanφt];

(6)

r2=rbexp[(θ-θ2)tanφt].

(7)

根据几何关系式可得式(8)～式(10):

(8)

(9)

(10)

式中:ra和rb为θ1和θ2的函数;θ3为θ1和θ2的函数.

4 计算过程

4.1 土体重力功率的计算

为了方便计算土体重力的功率,将破坏模式分成BHF和BFE这2个部分分别计算各自土体重力的功率,如图2所示.两部分土体重力的功率之和即为所求的土体重力功率.

在区域OHF中,土体重力的外功率可用式(11)计算.

(11)

其中函数f1(θ1,θ2)的表达式为

f1(θ1,θ2)=exp(3θ1){-3tanφt[exp(-3θ2tanφt)sinθ2-exp(-3θ1tanφt)sinθ1]-

exp(-3θ2tanφt)cosθ2+exp(-3θ1tanφt)cosθ2}/[3(1+9tan2φt)].

(12)

三角形区域OHB的土重做功的功率可用式(13)表示.

(13)

式(13)即三角形区域OHB的面积与土重γ与其重心处的速度在竖直方向的分量的乘积,其中函数f2(θ1,θ2)的表达式为

(14)

由此可得区域BHF土体重力做功的功率为区域OFH的土重做功的功率减去区域OHB的土重做功的功率,即:

W1=WOFH-WOHB.

(15)

对数螺旋线区域OBE的土体重力做功功率为

(16)

其中,函数f3(θ2,θ3)的表达式为

f3(θ2,θ3)={3tanφt[exp(3θ3tanφt)sinθ3-exp(3θ2tanφt)sinθ2] -exp(3θ3tanφt)cosθ3+

exp(3θ2tanφt)cosθ2}/[3exp(3θ2tanφt)(1+9tan2φt)].

(17)

对数螺旋线区域OFE的土重做功功率为

(18)

其中函数f4(θ2,θ3)的表达式为

f4(θ2,θ3)=exp(3θ1tanφt){-3tanφt[exp(-3θ3tanφt)sinθ3-exp(-3θ2tanφt)sinθ2]-exp(-3θ3tanφt)cosθ3+exp(-3θ2tanφt)cosθ2}/[3(1+9tan2φt)].

(19)

所以对数螺旋区域BFE的土体重力做功的功率可表示为

W2=WOFE-WOBE.

(20)

整个破坏模式土体重力做功功率为区域BHF与区域BFE两部分的土体重力做功的功率之和,即:

W=W1+W2.

(21)

4.2 掌子面围岩压力功率计算

σ0可简化成均匀分布,其做功功率可用式(22)计算:

(22)

式中:f5(θ1,θ2)的表达式如式(23).

(23)

4.3 内能损耗率计算

掌子面前方土体不同点的速度的大小和方向都不相同,内能损耗发生在两个速度间断面HE与BE上,速度间断面BE与HE上的内能损耗可分别由式(24)和式(25)计算.

(24)

(25)

(26)

(27)

破坏模式总的内能损耗功率为

D=DHE+DBE.

(28)

4.4 围岩压力的求解

根据外功率等于内能损耗率,则有

D=W+P.

(29)

将式(21)、式(22)和式(28)代入式(29),通过数学方法化简,计算,即可得到围岩压力的最终表达式为

(30)

式中:f1,f2,f3,f4,f5,f6,f7为θ1和θ2的函数.那么围岩压力σ0也为θ1和θ2的函数.

4.5 约束条件的确定

为求出式(30)的最大值,需要在一定的约束条件下对其进行优化,式中的物理参数要符合岩土体材料的特性,几何参数要具有实际的几何意义.综上,可确定约束条件如式(31).

(31)

结合上限定理,采用序列二次规划算法,通过Matlab软件编程来求解σ0的最优解.

5 结果分析

本文主要研究Baker准则中的3个参数A,T,n及埋深比C/D,土体容重γ对巷道破坏的影响.在计算中,各相关的参数取值为土体容重γ=20～24 kN/m3,C/D=1.0～2.0.无量纲参数A=0.4～0.8.T=0.01～0.05.n=0.5～0.9.计算结果如图3～图8所示.

图3 γ和C/D对围岩压力σ0的影响

图4 无量纲参数A和n对围岩压力σ0的影响

图5 无量纲参数A和n对围岩压力σ0的影响(T=0)

图6 无量纲参数T和n对围岩压力σ0的影响

图7 无量纲参数n和A对围岩压力σ0的影响

图8 无量纲参数A和T对围岩压力σ0的影响

埋深比C/D从1.0～2.0变化,土体容重γ分别为20,21,22,23,24 kN/m3条件下,C/D和γ对围岩压力σ0的影响见图3.从图3中可以看出:在γ相同的条件下,围岩压力几乎不随C/D变化;在C/D相同的条件下,围岩压力随γ的增加而增加.

当无量纲参数T=0.001 5,A从0.4～0.8变化,n分别为0.5,0.6,0.7,0.8,0.9条件下,A和n对围岩压力σ0的影响见图4.从图4中可以看出:在n相同的条件下,围岩压力σ0随着A的增加而减小;在A相同的条件下,围岩压力σ0随着n的增大而增大.在此特别讨论了当T=0时的情况,T=0为纯摩擦材料的强度准则(PF模型),见图5.结果表明T=0的变化规律和T≠0时基本相同.当无量纲参数A=0.5,T从0.01～0.05变化,n分别为0.5,0.6,0.7,0.8,0.9条件下,T和n对围岩压力σ0的影响见图6.从图6中可以看出:在n相同的条件下,围岩压力σ0随着T的增加而减小;在T相同的条件下,围岩压力σ0随着n的增大而增大.当无量纲参数T=0.001 5,n从0.5～0.9变化,A分别为0.4,0.5,0.6,0.7,0.8条件下,A和n对围岩压力σ0的影响见图7.从图7中可以看出:在T相同的条件下,围岩压力σ0随着A和n的增加而增加.当无量纲参数n=0.5,A从0.4～0.8变化,T分别为0.01,0.02,0.03,0.04,0.05条件下,A和T对围岩压力σ0的影响见图8.从图8中可以看出:在T相同的条件下,围岩压力σ0随着A的增加而减小;在A相同的条件下,围岩压力σ0随着T的增大而减小.

绘制了不同埋深比和无量纲参数A,T,n对破坏模式的形状的影响,结果如图9所示.

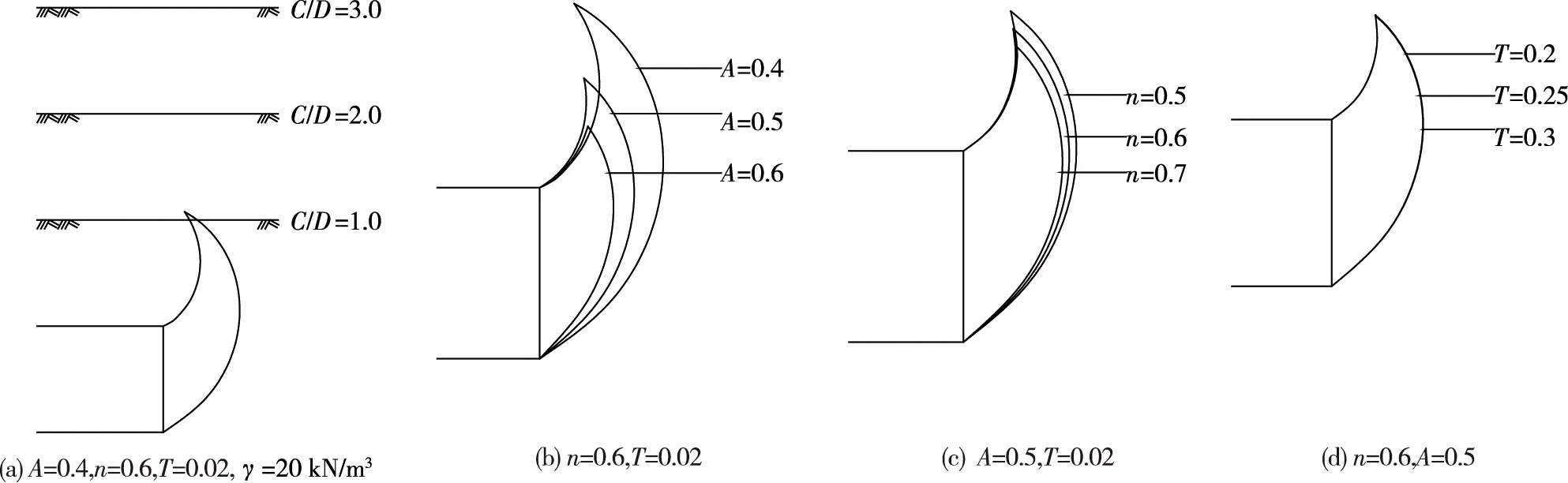
图9 各参数对破坏模式的影响

埋深比对破坏范围的形状影响如图9a所示,从图9a中可以看出,埋深比的变化并不会影响破坏范围的形状,但是会影响破坏范围是否会伸出地表.如果埋深比过小,破坏模式会在地面发生拱起破坏,最小埋深比应大于1.5.无量纲参数A,T,n对破坏模式的影响如图9b～图9d所示.从图中可以看出,当A减小时,破坏范围逐渐增大,由掌子面向前方外扩,破坏模式的形状由短胖变得狭长;当n逐渐增大时,破坏范围逐渐减小,与A不同的是,其主要影响的是“牛角”下方的范围,即影响破坏范围的深度；而T对破坏模式的形状基本无影响.

6 结论

1)非线性Baker准则的3个参数对围岩压力和掌子面破坏范围的影响各不相同.

2)随着A的增大,围岩压力非线性减小,破坏范围不断扩大.

3)随着n的增大,围岩压力非线性增大,破坏范围也呈增大趋势.

4)随着T的增大,围岩压力呈线性递减的趋势,破坏范围几乎无变化.