基于多元回归和BP神经网络的苎麻产量估测模型比较研究

王辉，付虹雨，王继龙，刘婕仪，崔丹丹，苏小慧，崔国贤*

（1.湖南农业大学苎麻研究所，湖南 长沙 410128；2.保险职业学院，湖南 长沙 410114）

农业是国民经济的重要组成部分，农作物生产对于社会的稳定具有重要作用。农作物产量是政府部门进行农业决策和宏观调控的重要依据，预估农作物产量具有重要意义［1］。由于影响农作物产量的因素较多，长期以来，如何快速、准确估测农作物产量一直是农业发展中面临的难题。现有的估产办法主要包括统计方法、遥感术、水肥测量、一元或多元回归分析等方法［2－4］，这些方法通常存在成本高、周期长、精确度不高等缺点，同时仅使用产量信息的预测方法无法得到更加准确的预测结果，而BP神经网络具有逼近复杂函数的良好能力，特别适用于分析产量与影响产量的众多因素之间复杂的线性和非线性关系，因此，在产量估测方面神经网络得到了广泛的应用［5－6］。

当前，国内学者主要在苎麻生理生化和栽培方面研究较多，而对于苎麻产量估测的研究较少。胡立勇等［7］结合多年实践对苎麻纤维产量计算方法进行总结分析，发现单位面积纤维产量与有效茎数、单株鲜茎重和鲜茎出麻率相关，且苎麻的株高、茎粗、鲜皮厚度对单株原麻产量有直接影响；陈坤梅等［8］通过相关分析法对几十份苎麻的产量和构成因子进行研究，指出苎麻株高、叶片数和分株数是苎麻育种可选择的重要指标，并构建了生物产量与主要影响因子的回归方程；孙丛苇等［9］基于降雨量和湿度数据，结合苎麻产量分别采用回归、神经网络和支持向量机等方法建立模型，结果发现模型除在产量预测方面具有较大实用性外，还可对病虫害进行预测。随着3S技术与精准农业的不断发展和推进，利用苎麻田间与产量相关的农艺性状数据，建立苎麻产量估测模型并验证，对苎麻高产提质意义重大。本文基于定位点苎麻（中苎1号）多年产量及其主要产量构成因素数据，采用多元回归和BP神经网络方法，分别建立产量估测模型，并验证和比较模型精度，旨在为定量估测苎麻产量提供一定的理论和技术依据。

1 材料与方法

1.1 材料和样地

试验所用苎麻种植于“湖南农业大学国家麻类长期定位试验基地”（113°04′E，28°10′N），该区气候属亚热带季风性湿润气候。试验品种为中苎1号（Zhongzhu No.1），由湖南农业大学苎麻研究所提供。2009年6月7日将育好的麻苗移栽到长期定位试验小区，设1个处理，4次重复，小区面积约20.00 m2（小区长、宽分别为7.50、2.67 m），其中每小区定56穴，每穴2株秧苗。经测定，供试基地土壤含全氮 1.3 g／kg、碱解氮 81.7 mg／kg、速效钾 148.0 mg／kg、速效磷 83.4 mg／kg、有机质25.0 g／kg。

1.2 数据来源

以中苎1号产量及其主要农艺性状数据为研究对象，品种4次重复，测定项目和方法见下表1，每年收获3次，数据详情如表2所示。长期以来专家和学者将株高、茎粗、皮厚、有效分株数、出麻率一起称为苎麻的五大产量构成因素［10］。孙学兵［11］通过对苎麻主要农艺性状和纤维产量与品质的分析和研究，发现株高、茎粗、出麻率3个因素是构成纤维产量的关键因子，其中株高对产量和品质表现出最大正向或负向贡献，但鲜皮厚度则刚好与之相反。结合领域专家意见和生产经验，本文选取了苎麻株高、茎粗、分株数、有效株率和鲜皮厚度5个产量构成因素来构建苎麻的BP神经网络产量估测模型。由于部分年份遭遇极端天气造成部分小区苎麻倒伏，导致减产，因此出现同一季麻中不同小区的产量数据存在较大差异的情况。

表1 测定项目及方法Table 1 Determination items and methods

表2 2010～2019年中苎1号产量及其产量构成因素Table 2 The yield and yield components of Zhongzhu No.1 during 2010－2019

续表2

续表2

续表2

1.3 数据处理

采用Excel 2010和DPS（v7.05）软件对数据进行处理。

1.4 多元回归模型

多元线性回归分析是基于现实数据获取各相关变量间联系的统计方法，常被应用于通过已有数据构建线性回归模型，从而实现对数据变化趋势的预测［14－15］。该模型在农作物产量预测方面得到了广泛的应用［16］，是一种较为成熟的预测模型。由于苎麻产量的主要构成因素有株高、茎粗、分株数、有效株率、鲜皮厚度，所以将上述5个产量构成因素纳入建立的苎麻产量回归模型中，结合表2的中苎1号9年间（2010～2018年）27个收获期（每年3季）108组原始样本数据，为增加样本量，将各收获期数据综合一起进行回归，得到苎麻产量与产量构成因素之间的线性回归模型如下：

式中：Y为苎麻产量，文中涉及的苎麻产量有2个，一个是鲜皮产量Y1（103kg／hm2），另一个是原麻产量 Y2（102kg／hm2），分别建立两个产量与产量构成因素（X1，X2，…，X5）的多元回归方程；其中：X1，X2，…，X5分别表示株高（m）、茎粗（cm）、分株数（104株／hm2）、有效株率（%）和鲜皮厚度（mm），α为随机参数，β1，β2…，β5为待定系数。

1.5 BP神经网络模型

1.5.1 BP神经网络的结构

BP（Back Propagation）神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，该算法即称BP算法［17－18］。BP神经网络由输入层、隐含层和输出层组成，含多层神经元。

1.5.2 BP神经网络运行原理

三层神经元的BP神经网络运行步骤如图1所示。

（1）网络权值与阈值的初始化

在数据进行归一化处理后，对神经元的各权值wij和 νij，阈值 θj和 γj赋予区间（－1，1）内的随机值，其中：wij，I＝1 2，…，p，j＝1，2，…，p：输入层至中间层的连接权；νij，I＝1，2，…，p，t＝1，2，…，p：中间层至输入层的连接权；θj，j＝1，2，…，p：中间层各单元的输出阈值；γj，j＝1，2，…，p：输出层各单元的输出阈值。

（2）给定试验样本

结合样本数据向量X1，X2，… Xn和Y1，Y2，… Ym，随机选取一组输入和目标样本，记作：

（3）中间层输入／输出计算

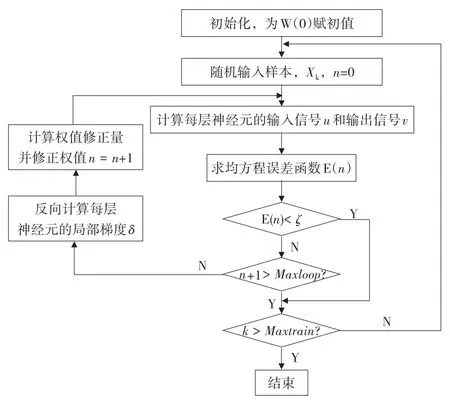
图1 BP神经网络算法流程Fig.1 The algorithm flow of BP neural network

式中，sk＝（s1，s2，…，sp）：中间层单元输入向量；Bk＝（b1，b2，…，bp）：输出向量，j＝l，2，…，p。

（4）输出层输入／输出计算

利用中间层的输出bj、连接权νij和阈值γj计算输出层各单元的输入Lt，然后通过传递函数计算输出层各单元的响应Ct。

式中，Lk＝（l1，l2，…，lq）：输出层单元输入向量，Ck＝（c1，c2，…，cq）：输出向量，t＝l，2，…，q。

（5）输出层一般化目标计算

式中，t＝1，2，…，q。

（6）中间层一般化目标计算

（7）连接权与阈值计算

利用输出层各单元的一般化误差dkt与中间层各单元的输出bj来修正连接权νij和阈值γj。

其中t＝1，2，…，q；j＝l，2，…，p；0＜a＜1。这样，输出层连接权和阈值便在中间层各单元的输出和输出层一般化目标的作用下得到一次修正。

（8）连接权与阈值修正

其中i＝1，2，…，q；j＝1，2，…，p；0＜β＜1。这样，中间层连接权和阈值便在中间层输出和中间层各单元的一般化目标的作用下得到一次修正。

（9）学习样本的选取

当数据样本学习完成后，网络将随机对其他样本按照上述（3）步骤进行学习，直至所有样本结束。

（10）全局误差E的判断

重新从m个学习样本中随机选取一组输入和目标样本，返回步骤（3），直到网络全局误差E小于预先设定的一个极小值，即网络收敛。

（11）学习训练完成［19］。

1.5.3 BP神经网络产量估测模型构建

运用MATLAB软件编程，以定位点试验10年数据构建苎麻产量与对应收获期内产量构成因素的BP神经网络产量估测模型。通过隐含层节点数的比对，结合数据变量和研究目标的特点，设定神经网络模型的隐含层为2层，各层节点数为5个，神经网络的具体结构如图2所示。隐含与输出层的传递函数选定tansig和pureline函数，学习函数为traingd函数，训练次数为6000次，以此作为预测苎麻产量的最优模型，由于BP神经网络需要较大样本量，所以，为增加样本容量，将历年各收获期的108组原始样本数据（见表2）综合在一起作为训练数据。

图2 神经网络结构示意Fig.2 Schematic diagram of neural network structure

2 结果与分析

2.1 多元线性回归模型估测

通过DPS软件对表2数据进行多元回归分析，得到中苎1号鲜皮产量和原麻产量回归模型为：

式中：

Y1—鲜皮产量，103kg／hm2；

Y2—原麻产量，102kg／hm2。

2.2 BP神经网络产量模型估测

通过网络学习和训练，当神经网络的学习次数Epoch为6000次，学习速率lr为0.05时，中苎1号的MSE值最小，收敛于0.0119，如下图3所示，说明此时神经网络训练的效果较好，获得了较为稳定和理想的结果。通过BP神经网络模型对样本数据训练，得到中苎1号鲜皮产量和原麻产量预测模型训练的各项误差指标，具体如表3所示。

图3 中苎1号神经网络训练图Fig.3 Neural network trainingmap of three ramie varieties

表3 BP神经网络产量估测模型误差Table 3 Fitting error of ramie yield and prediction value based on BP neural network model

为进一步验证产量预测模型的模拟效果，在MATLAB程序编写中，选用表2中苎1号2010～2018年27个收获期共计108组原始样本数据作为训练数据，同时以2019年不同收获期的12组真实产量作为验证数据，根据训练好的模型对2019年苎麻产量进行估测，将得到的估测产量与真实产量进行比对，效果如图5所示。从图中可以看出，神经网络模型下获取的中苎1号鲜皮产量和原麻产量的估测值与真实值拟合效果整体较好。

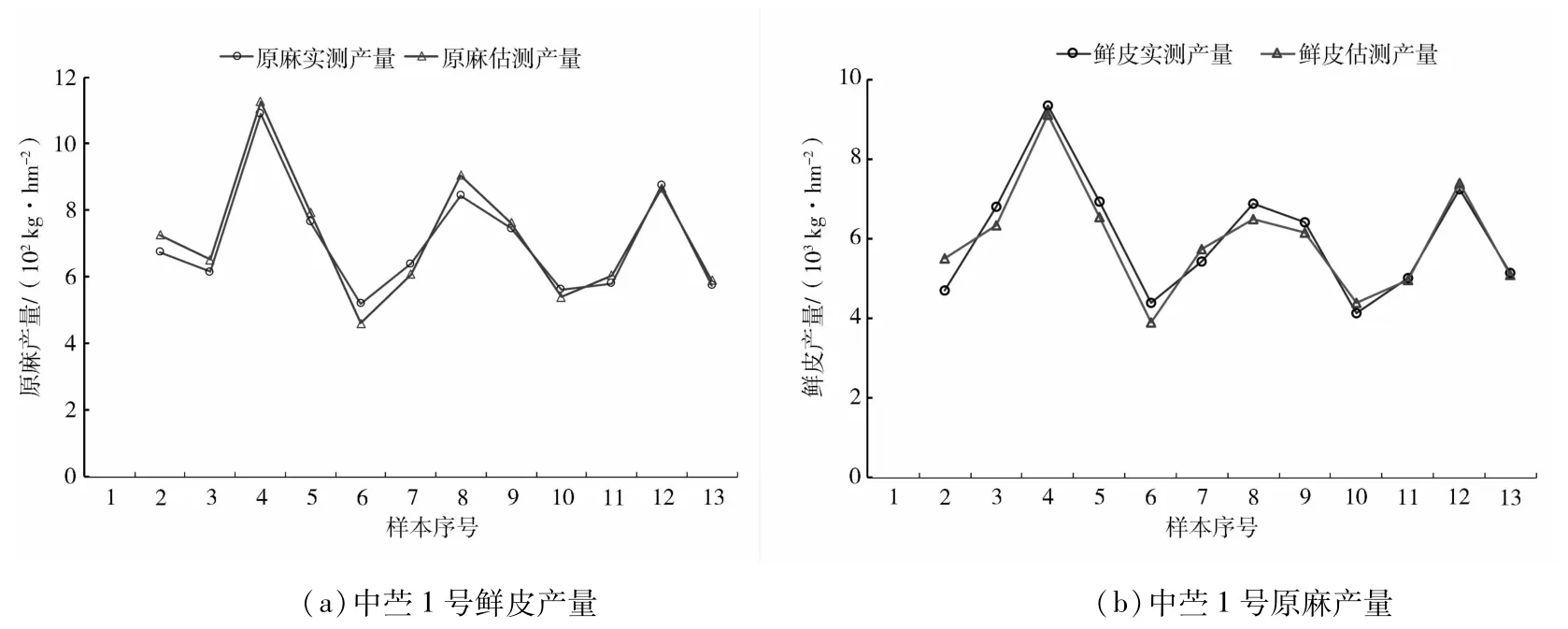
图4 2019年中苎1号产量预测拟合情况Fig.4 The forecast of the yield of Zhongzhu No.1 in 2019

2.3 估测结果对比分析

通过构建的回归模型和BP神经网络获取中苎1号2019年的12组估测产量，将其与当年实际产量进行对比，结果如下表4、5所示。整体来看，基于BP神经网络方法估测的中苎1号产量，在误差差异和稳定性方面明显优于多元线性回归方法。回归方法中，中苎1号鲜皮产量和原麻产量估测值与真实值间的绝对系数R2分别为0.40和0.47，相对误差分别在5.05%～46.60%和1.18%～39.69%范围内波动，平均相对误差分别为15.03%和14.52%；鲜皮产量和原麻产量中均有多组估测数据误差超过20%以上，回归模型估测的整体效果均较差且波动都较大。

BP神经网络方法中，中苎1号鲜皮产量和原麻产量估测值与真实值间的拟合系数R2分别为0.93和0.97，相对误差分别在0.80%～17.23%和1.14%～11.54%范围内波动，平均相对误差分别为5.78%和4.88%。基于BP神经网络方法估测获取的中苎1号产量相对误差值绝大部分都低于6%，且波动较小，其中鲜皮产量仅有2019年头麻和二麻中各有一组数据超出10%，原麻产量仅二麻中有一组数据超出10%，说明BP神经网络模型估产的稳定性和精度都较好，估测效果明显优于多元回归模型，该BP神经网络估测模型适用于苎麻产前的产量估测。

表4 中苎1号鲜皮产量估测结果对比Table 4 Comparison of prediction results of fresh skin yield of Zhongzhu No.1

表5 中苎1号原麻产量估测结果对比Table 5 Comparison of prediction results of yield of Zhongzhu No.1

3 讨论与结论

苎麻堪称我国服用麻纤维当中的“国宝”，苎麻的增产提质对我国苎麻产业的稳定发展有着重要意义［20］。通过对苎麻产量和产量构成因素的相关性进行分析，建立苎麻的产量估测模型，提前估测苎麻产量，对苎麻田间管理和种植效益的提升都有着积极促进作用。本文分别采用多元线性回归和BP神经网络两种方法，利用多年定位试验下中苎1号的产量和产量构成因素相关数据构建产量估测模型，并对其2019年鲜皮产量和原麻产量进行了估测，通过对两种方法估测的结果进行对比分析发现：利用多元回归方法建立的苎麻产量估测模型得到的估测值误差值整体偏大，且波动较大，稳定性不强，有多组数据的绝对误差值均超过20%以上；而BP神经网络方法获取的苎麻产量估测值在精度和稳定性方面明显优于多元线性回归模型，模型整体预测效果较好，拟合值R2均在0.93以上，且均方误差（MSE）均低于0.14，优于孙丛苇等［9］研究中支持向量机（SVR）、多元回归和BP神经网络获取的最高精度，R2分别为0.73、0.66和0.83，MSE分别为0.21、0.26和0.27；也优于付虹雨［21］等利用无人机遥感图像估产精度，R2为0.85，证明利用BP神经网络方法构建产量估测模型的方法比多元回归方法更适用于苎麻的产量估测，且估测的精准度和稳定性较好，这与梁姝娜等［22］、高亮亮等［23］和李蓬勃等［24］研究结果一致。

从BP神经网络模型估测的苎麻产量与实际产量对比结果来看，整体估测的相对误差均值不高，基本在5%上下波动，但存在一些相对误差较大的数值，导致该结果的原因很可能是因为模型构建时选取了苎麻株高、茎粗、分株数、有效株率等5个主要产量构成因素作为变量，虽然他们是苎麻产量的主要决定因素，但外界因素对苎麻产量和产量构成因素也有一定的影响［25－27］，而BP神经网络估测模型中未将这些外界影响因素纳入，从而使得估测结果出现部分数据误差较大的情况；另外，在选取BP神经网络训练和学习样本数据时，虽然样本数据量达到108组，但是真正跨年度的样本量仅有9年，从年度来看样本数据量仍偏少，因此在BP神经网络产量模型进行训练时会带来一定影响，使得模型在产量预测时出现误差的可能性增大。