基于ARIMAX模型的水泥稳定碎石基层温度预测方法

康爱忠，苏丽娜，冯 琦

(中电建冀交高速公路投资发展有限公司，河北省石家庄市桥西区城角街672号 050051)

水泥稳定碎石基层路用性能受养护温度影响较大，而基层实际养护温度与大气温度、地表温度等因素密切相关。在实际工程中，由于温度变化容易使水泥稳定碎石基层产生裂缝，导致基层路用性能降低。然而，基层温度难以直接量测，通常需将传感器埋设在基层内而获得，因此，铺设基层前通过量测大气温度和地表温度准确地预测水泥稳定碎石基层温度，确定基层施工工艺可以在不利的温度条件下保障其路用性能。

郭学东等[1]对季节性冻土地区路面温度场进行研究，对沥青路面任意深度的温度建立回归预估模型，此模型可用于预测水泥稳定碎石基层温度。梁乃兴等[2]探究了云南大理区某高速公路一天内沥青路面不同深度处温度变化，并建立预测模型，该模型可预测水泥稳定碎石基层温度在一天内的变化。现有文献表明，研究人员多集中于对已建成的路面结构进行研究，建立可用于预测水泥稳定碎石基层温度的模型。但是没有人对基层施工期的早期温度进行研究，没有人在基层摊铺前建立对水泥稳定碎石基层温度进行预测的模型。

针对上述问题，文中以大气温度和地表温度为输入序列，水泥稳定碎石基层温度作为响应序列，借助Eviews9[3]软件对每个输入序列进行平稳性检验，依据AIC和SC准则对每个平稳序列建立ARMA预测模型，每个ARMA模型的残差序列通过白噪声检验后，再采用最小二乘拟合估计法建立用于预测水泥稳定碎石基层温度的ARIMAX模型[4]。最后，利用相对误差百分比公式检验实际数据和预测数据的误差。结果表明该模型拟合良好，预测准确度高。

1 ARIMAX模型的理论基础

ARIMA模型可对未来进行预测，但该模型只可对某一个时间序列进行分析，对一些实际问题的使用有限制，不能满足现实生活中多个时间序列影响的需求。而ARIMAX模型含有多个输入变量序列和响应序列，在实际问题中可以综合考虑多个因素对响应序列的影响，因此该模型提高了预测的精准度，应用也日益广泛。文中拟对水泥稳定碎石基层温度进行预测，其影响因素包括大气温度和地表温度，因此选用ARIMAX模型。

1976年，Box George E P等人[5]采用带自变量的ARIMAX模型对时间序列进行预测，但这一模型要求输入序列与响应序列皆为平稳序列。1987年，Engle R F等人[6]对以上ARIMAX模型进行调整，提出只需要输入序列和响应序列的回归残差序列平稳即可，使该模型得到了优化，不仅减少了限制条件，也提高了模型预测的精确度。

(1)

式中：Φi(B)是第i个输入变量的自回归系数多项式；Θi(B)为第i个输入变量的移动平均系数多项式；li为第i个输入变量的延迟阶数；εt为回归残差序列。

由于{yt}和{xit}(i=1,2,…,k)都是平稳序列，经过线性组合依旧平稳，所以残差序列εt也为平稳序列：

(2)

结合ARMA模型，通过提取残差序列εt中的信息，得到如下ARIMAX模型:

(3)

式中：Φ(B)为残差序列自回归系数多项式；Θ(B)为残差序列移动平均系数；at为零均值白噪声序列。

2 基于ARIMAX模型的水泥稳定碎石基层温度预测

2.1 数据来源与处理

为掌握水泥稳定碎石基层温度状况，在112线试验路基层埋设温度传感器并进行了长期的温度观测后得到基层温度序列，并且将基层顶面的温度定义为地表温度。文中选取2019年11月13日至2019年12月6日所量测的路基温度、地表温度及大气温度作为研究数据。

ARIMAX模型可实现多输入序列对响应序列的预测，文中将输入变量序列地表温度和大气温度分别记为{x1t}，{x2t}，响应序列基层温度用{yt}表示；x1与x2表示对地表温度和大气温度取一阶差分，lny表示对路基温度取对数后再取一阶差分后的数据。利用Eviews9软件对2019年11月13日至2019年12月6日的路基温度、地表温度及大气温度的23组数据画序列图，从视觉上初步判断原数据序列平稳与否，见图1、图2。

图1 原数据序列图Fig.1 Original data sequence diagram

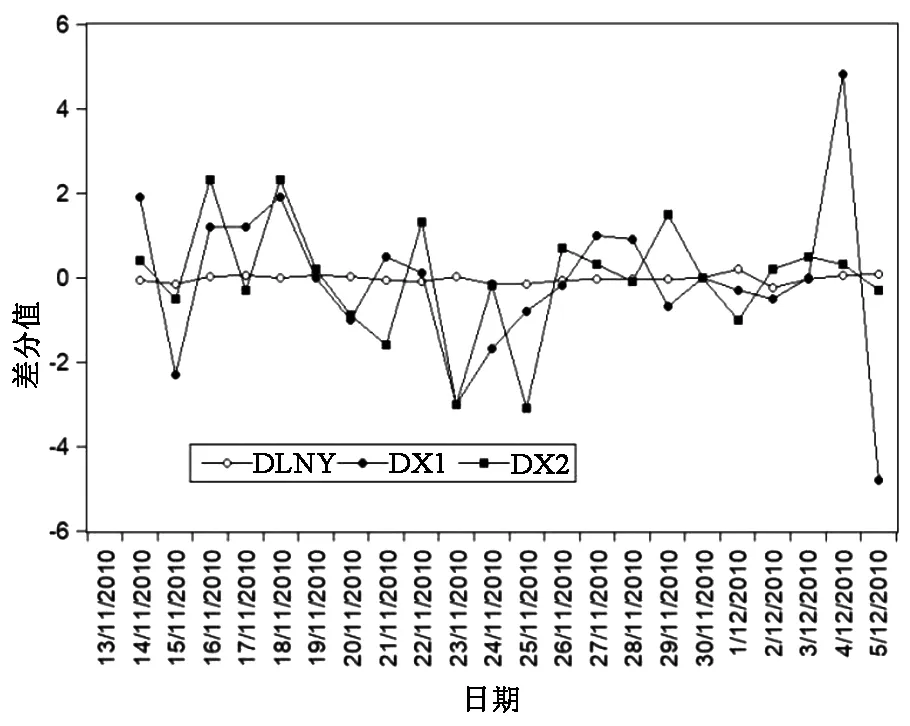
图2 lny，x1和x2图Fig.2 lny，x1 and x2 diagram

图1显示响应序列y明显下降，是一个非平稳序列；输入序列x1，x2都呈现先上升后下降的趋势，不能确定为是平稳序列，需要对x1，x2进行处理。因此对输入序列和响应序列进行适当运算，对x1，x2直接进行1阶差分得到x1与x2；对y取对数后进行1阶差分，得lny。图2显示与x1，x2，lny序列无明显趋势，可初步将运算后的序列认定为平稳序列，但还需要进一步确定序列的平稳性。

2.2 ADF平稳性检验

文中借助Eviews9软件(View-Unit Root Test)对原数据序列x1，x2，y以及经过运算后的序列x1，x2，lny分别进行ADF检验[11]，结果如表1所示。假设H0：序列为非平稳序列。由表1可知，序列x1，x2，y均为平稳序列。

数学思想是内隐的,数学方法是数学思想的表现形式和得以实现的手段．数学思想比数学方法更深刻、更抽象地反映了数学对象间的内在联系[3]．笔者认为,数学思想形成的前提是让学生经历应用的历练,而教师提供时间与空间是“方法”提升为“思想”的保证．为了促使学生更好地感悟数学的思想方法,提升数学的思维能力,教学中就需要教师进一步的引领和学生群体的互动．

表1 ADF检验结果Tab.1 Results of ADF test

2.3 输入序列建模

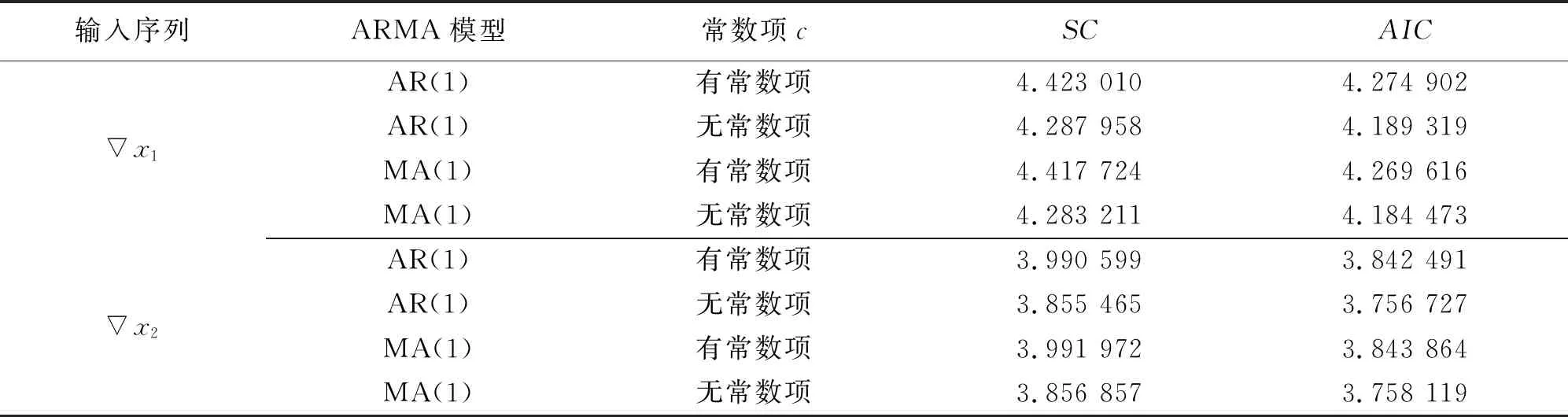
表2 输入序列可能拟合情况Tab.2 Possible fitting of input sequences

表2直观地展示了输入序列所拟合的可能模型的SC值与AIC值，依据SC和AIC原则，确定输入序列x1，x2拟合的模型均选择无常数项，具体模型为

x1=(1-0.309152B)εt

(4)

(5)

(a)x1

2.4 建立ARIMAX模型

(a)lny与x1

图4lny与x1，x2互相关系数图
Fig.4 Interrelation number diagram oflnyandx1，x2

(6)

利用最小二乘拟合估计，拟合该ARIMAX模型，回归模型为

(7)

AIC=-4.339683，SC=-4.142206，R2=0.935046，S.E.=0.025549，残差序列的自相关和偏相关关系如图5所示。

图5 残差的自相关和偏相关图Fig.5 Autocorrelation and partial correlation of residuals

图5显示：所拟合模型残差的自相关系数显著为零;偏相关系数表明x1与x2残差的互相关系数显著为零，该残差序列为白噪声序列并且可以通过ADF检验，即所建立的ARIMAX模型充分提取了信息，拟合良好。

2.5 模型预测与拟合

以2019年11月14日到2019年12月5日的大气温度和地表温度为数据基础，利用ARIMAX模型对112线试验路的水泥稳定碎石基层温度进行预测。将预测值与量测的实际值进行比较，利用误差百分比来表示预测精确度，结果如表3所示。

表3 基于ARIMAX模型水泥稳定碎石基层温度预测结果Tab.3 Prediction results of cement stabilized gravel base temperature based on ARIMAX model

由表3可知，根据ARIMAX模型预测的基层温度和实际量测的基层温度计算所得的误差百分比均未大于0.1%，2019年11月14日至2019年12月5日的22组数据的平均误差百分比为-0.04198%，在0.05%范围内，说明基于ARIMAX模型预测的水泥稳定碎石基层温度与实际值非常相近，即该模型所预测的准确度非常高。为更加直观地观察回归模型的拟合效果，得到最终的拟合图见图6。

图6 水泥稳定碎石基层温度实际值与预测值拟合Fig.6 Fitting of actual and predicted temperatures of cement-stabilized gravel base

3 结论

文中对输入序列大气温度和地表温度进行适当运算后得到平稳序列，依据最小AIC准则分别建立ARMA模型，利用Eviews9软件对残差序列进行检验得到平稳白噪声序列，最后结合最小二乘拟合估计方法，将2个ARMA模型拟合为用于预测水泥稳定碎石基层温度的回归动态模型——ARIMAX模型。

(1)路面基层温度受大气温度和地表温度的综合影响，若将每个因素和基层温度单独建模，只考虑单个因素对水泥稳定碎石基层温度的影响，所得到的预测模型对路面基层温度预测不准确。

(2)利用ARIMAX模型对水泥稳定碎石基层温度进行预测，每组实际值和预测值的误差百分比不大于0.1%，平均误差百分比为-0.04198%，可知该模型预测精准度很高。

(3)若想要进一步提高预测值的精准度，应扩大量测日期的范围，获得更多的数据来建立预测模型。