电力假数据注入攻击的残差检测方法效率分析

武津园, 王 勇, 刘丽丽, 程彦喆

(1.上海电力大学 计算机科学与技术学院, 上海 200090;2.华电电力科学研究院有限公司 国家能源分布式能源技术研发(实验)中心, 浙江 杭州 310030;3.东南大学 网络空间安全学院, 江苏 南京 210000)

现代电网具有规模大、层次复杂、网络拓扑多样、对实时性要求严格等特点。随着电网的智能化发展,电力系统对计算机信息技术的依赖程度越来越高,物理元件和网络的交互,使得电网正在演变为一个电力信息物理系统(Cyber Physical System,CPS)[1]。大量传感设备和集成的通信网络使系统具有实时感知、信息服务和动态控制功能[2]。数据采集与监视控制(Supervisory Control and Data Acquisition,SCADA)系统是以计算机为基础的电力系统生产过程控制与调度自动化系统,可以对现场运行设备进行监视和控制[3]。电力系统设计之初并没有充分考虑到网络的安全因素,因此物理系统与信息系统的深度融合使得传统物理攻击及网络攻击能够协同作用,给电网带来了新的安全隐患[4-5]。LIU Y等人[6]于2009年首次提出了假数据注入攻击(False Data Injection Attack,FDIA),通过破坏数据完整性干扰决策。攻击者在对电力网络拓扑结构部分了解的前提下,通过向分布在电网中的计量装置注入虚假数据,影响电力系统正常运行的同时,成功躲过坏数据检测机制,达到危及电力系统安全的目的[7]。FDIA对电力系统状态估计[8](State Estimation,SE)有致命影响,导致电网控制中心的误判,进而可能导致电网大停电事故,造成重大的国民经济损失。由于假数据注入攻击对智能电网的危害性较大,隐蔽性较强,在学术界受到了广泛关注[9]。作为针对基础工业控制系统的新型攻击方式,网络攻击已成为电力系统维护安全稳定运行不容忽视的威胁,其攻击机理、检测方法、防御手段及相应的安全态势评估方法亟待研究[10-11]。

当下存在的主要问题是:假数据注入攻击发生在高度耦合的环境下,自信息网络的威胁导致物理系统恶意破坏,引发一系列的连锁事故;需要在制定虚假数据入侵检测策略时,充分考虑检测算法的时效性、灵敏性和抗扰动性。本文结合CPS分析了虚假数据注入的原理,并结合攻击原理和两种传统的恶意数据检测方法,设计了一种实验方案,从大量且不重复的对IEEE拓扑结构单点假数据注入攻击中,验证了理论的正确性,进一步表明传统检测方法对假数据的局限性。

1 问题描述

FDIA是一种针对电力系统状态估计的蓄意攻击。假数据是由攻击者为了毁坏系统或应用而恶意构建的。

1.1 检测模型

在电力系统不良数据检测中,状态估计表达式为

J(x)min=[z-H(x)T·Wz-H(x)]

(1)

式中:J(x)min——估计表达式;

z——测量值;

H(x)——由各状态量x和节点导纳矩阵表示的各测量值的函数关系;

W——权重。

测量值中可能带有坏数据,为了避免可能因源自故障传感器、拓扑误差等带来的不良测量,检测机子需要将J(x)与预先设定的阈值τ进行比较。如果J(x)小于阈值τ,则认为没有不良数据,反之要剔除相应的坏数据,对系统重新进行状态估计。

1.2 CPS中的虚假数据注入

CPS的虚假数据注入攻击,主要集中于输电、配电、用电系统。对其检测逐渐从依赖操作人员经验转向为依赖自动化数据采集和检测系统[12]。CPS是一个综合计算、网络和物理环境的多维系统,可以实现计算、通信和控制的一体化。典型的CPS框架如图1所示。

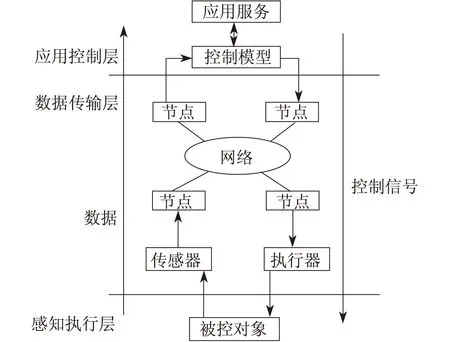
图1 典型CPS框架示意

由图1可知,CPS框架可划分为3层:感知执行层、数据传输层和应用控制层[13]。CPS以通信网络为核心,网络规模和分布式的信息处理环境使得CPS容易受到虚假数据攻击。在电力系统中引入网络特性,入侵者能通过FDIA将判断结果指向不需要的控制命令,从而导致系统无法执行合理指令,甚至使电力系统系统陷入不可控的状态。

2 攻击检测方法

目前常用的攻击检测方法主要是基于量测数据残差的方法,包括目标函数检测法、rW检测法和rN检测法[14]。

2.1 目标函数检测法

rTR-1r

(2)

式中:R——m×n阶量测误差方差矩阵。

假设第i个测量值存在不良数据,数据值为ai,量测误差矢量可表示为

v=vz+eiai

(3)

式中:vz——正常量测条件下的m维量测误差矢量;

ei——m维单位矢量。

于是有

(4)

式中:vwz——正常量测条件下的m维加权量测误差矢量;

WW——加权残差灵敏度矩阵;

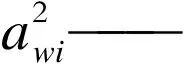
等式右端第一项是正常量测条件下的目标函数极值J(x),第二项为0均值的正态分布,第三项为常数项,故统计特性为

(5)

式中:E——期望值;

K——阶数;

ww,ii——影响系数。

2.2 rW检测法与rN检测法

rW检测法是通过比较残差的加权形式是否超过阈值来检测不良数据。将rW表示为

(6)

式中:WW,ij——WW的对角元素;

vwj——加权量测误差矢量。

正常量测条件下Evwz,j=0,Erwz,i=0,加权残差服从0均值的正态分布。加权残差的方差表示为

(7)

式中:zwz,i——加权残差法中的测量值;

rwz,i——加权残差法中的残差。

综上可得,rwz,i～N(0,Ww,ii)。根据数理统计,rW检测法将每一维测量值按假设检验方式进行,具体为

(8)

式中:γw,i——第i个加权残差的门槛值。

与rW检测法类似,rN检测法是通过检验标准化残差rN来检测不良数据。残差方程的标准化形式为

rN=WNv

(9)

式中:WN——残差灵敏度矩阵;

v——量测误差矢量。

类似rW检测法,rN检测法按如下形式进行:

(10)

式中:γN,i——第i个标准化残差的门槛值。

2.3 效率分析

FDIA是对单个或多个量测添加可以躲避残差检测的随机误差,使状态估计器误认为是好的数据,达到操纵状态估计准确性的目的。

添加到原始测量值中的非零攻击矢量为

a=(a1,a2,a3,…,am)T

(11)

导致新的测量值za=z+a产生偏差。

将新的测量值za发送到状态估计器,导致带有偏差的估计为

(12)

c——非零向量,表示恶意注入对状态估计的影响。

将攻击矢量构造为

a=Hc

(13)

则:

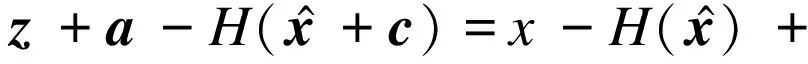
(14)

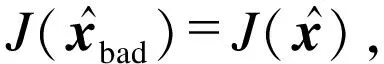
3 实验分析

本文提供了一种对单点注入的虚假数据攻击进行检测的实验方法。通过MATLAB软件编程实现,数据采用matpower 4.1电力仿真数据包中的IEEE 30与118节点系统的拓扑数据。

3.1 IEEE 30节点系统仿真实验

IEEE 30节点系统拓扑结构如图2所示。

图2 IEEE 30节点系统拓扑结构

在IEEE 30节点系统的潮流参数中,在数据编号为20的节点处注入虚假数据,具体如图3所示。

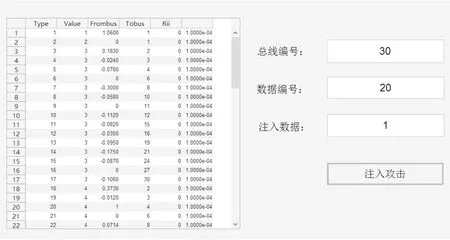
图3 在数据编号为20的节点处注入虚假数据

利用电力系统恶意数据检测方法,对注入了虚假数据的位置参数进行检测,并绘制目标函数、标准化残差检测结果和目标函数检测结果如图4所示。

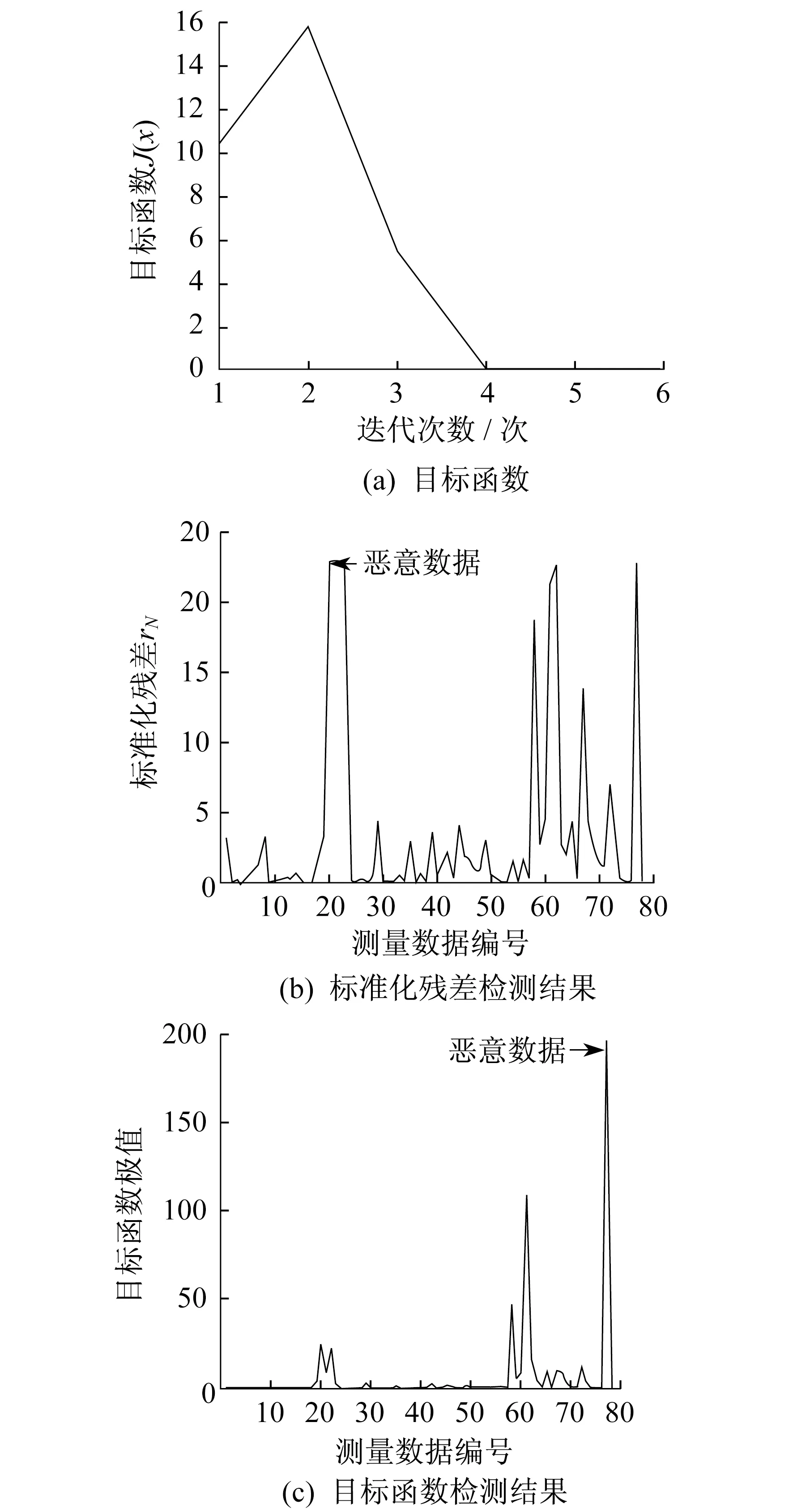
图4 IEEE 30节点系统虚假数据注入下的检测结果

检测结果表明,经过目标函数6次迭代,图4均显示检测出了虚假数据。在图4(b)中,虚假数据标注在20号,在图4(c)中,虚假数据标注在79号,与注入数据编号不符,说明在目标函数检测结果中发生了误检现象。

3.2 IEEE 118节点系统仿真实验

IEEE 118节点系统拓扑结构如图5所示。

在IEEE 118节点系统的潮流参数中,在数据编号为10的节点处注入虚假数据,具体如图6所示。

图5 IEEE 118节点系统拓扑结构

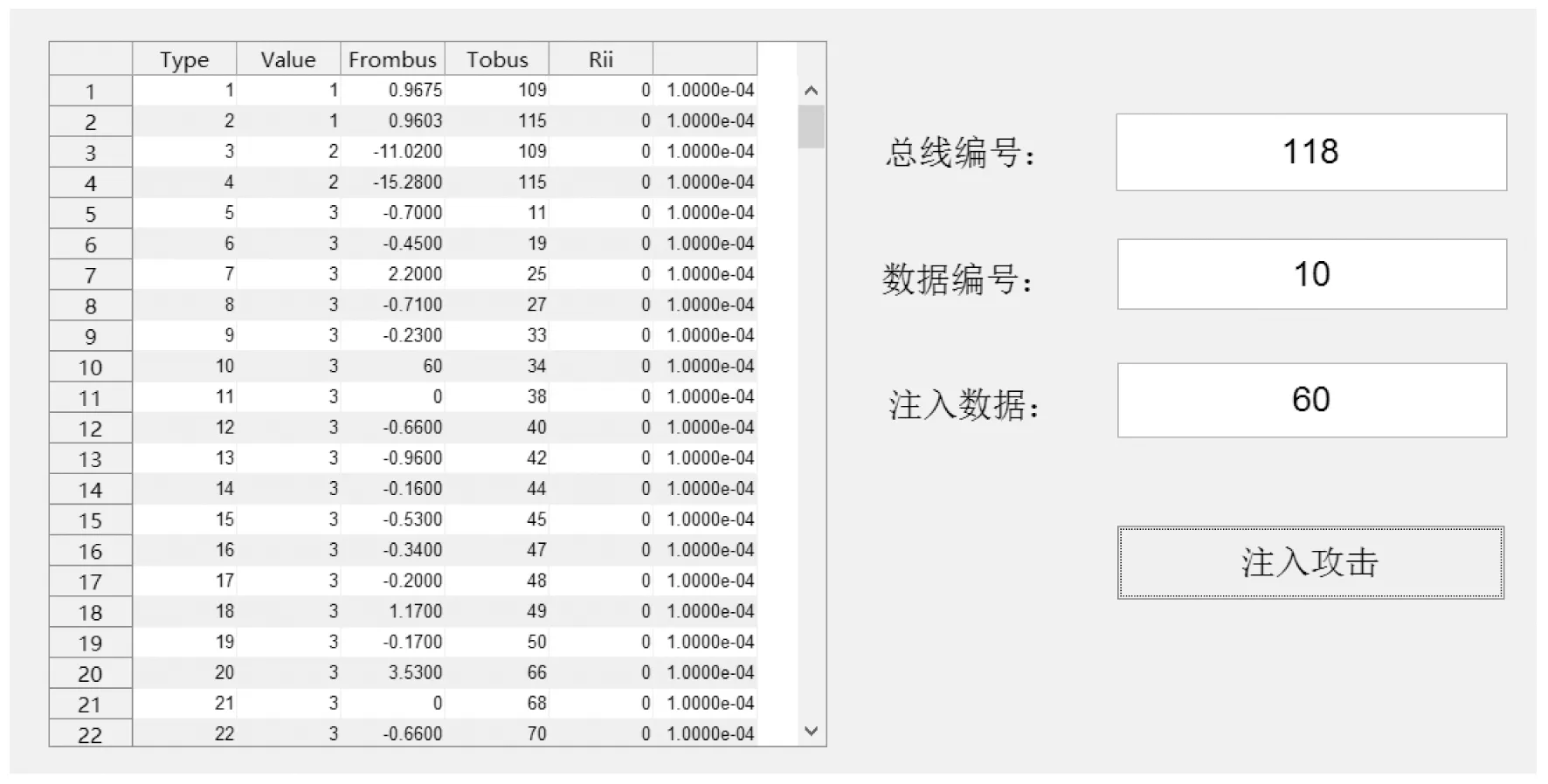
图6 在数据编号为10的节点处注入虚假数据

同样利用电力系统恶意数据检测方法,对注入了虚假数据的参数进行检测,并绘制目标函数、标准化残差检测结果和目标函数检测结果,具体如图7所示。

如图7可知,在标准化残差和目标函数检测结果中均未显示检测出了虚假数据,发生了漏检现象。

4 结果分析

文中使用的实验方法,可以在IEEE 30与IEEE 118节点系统的任意数据节点上注入任意数值的虚假数据,实现对系统的单点攻击。从上述实验分析可以看出,检测存在漏检和误检两种情况。在每个节点中分别注入数据,反复进行实验,统计对虚假数据注入检测的错误率,系统检测结果如图8所示,其中0代表检测失败,1代表标准化残差方法检测成功,2代表目标函数方法检测成功。

从图8(a)中可以看出,在IEEE 30节点系统的多次实验中,标准化残差法和目标极值法的成功检出率与理论证明相符合,说明传统检测方法对假数据的注入并不灵敏。从图8(b)中可以看出,相比IEEE 30节点系统,两种方法的成功检出率有所提升,但仍存在很高的错误率。

分别对两种系统进行攻击,在IEEE 30节点系统中进行35次节点的单点攻击,每个数据编号攻击两次,其中首次注入的虚假数据偏差较小,第二次数据较原始数据偏差较大,检测结果发生了漏检、误检以及少量无法检测的情况。在IEEE 118节点系统中,选取前35个数据编号,注入同样数值大小的假数据,检测结果同样发生了漏检和误检的情况。

网络入侵检测系统的指标主要包括3类,即检测率、误报率和漏报率。

检测率是受到虚假数据入侵攻击时,系统能够正确报警的概率。通常利用已知入侵攻击的实验数据集合来测试系统的检测率。

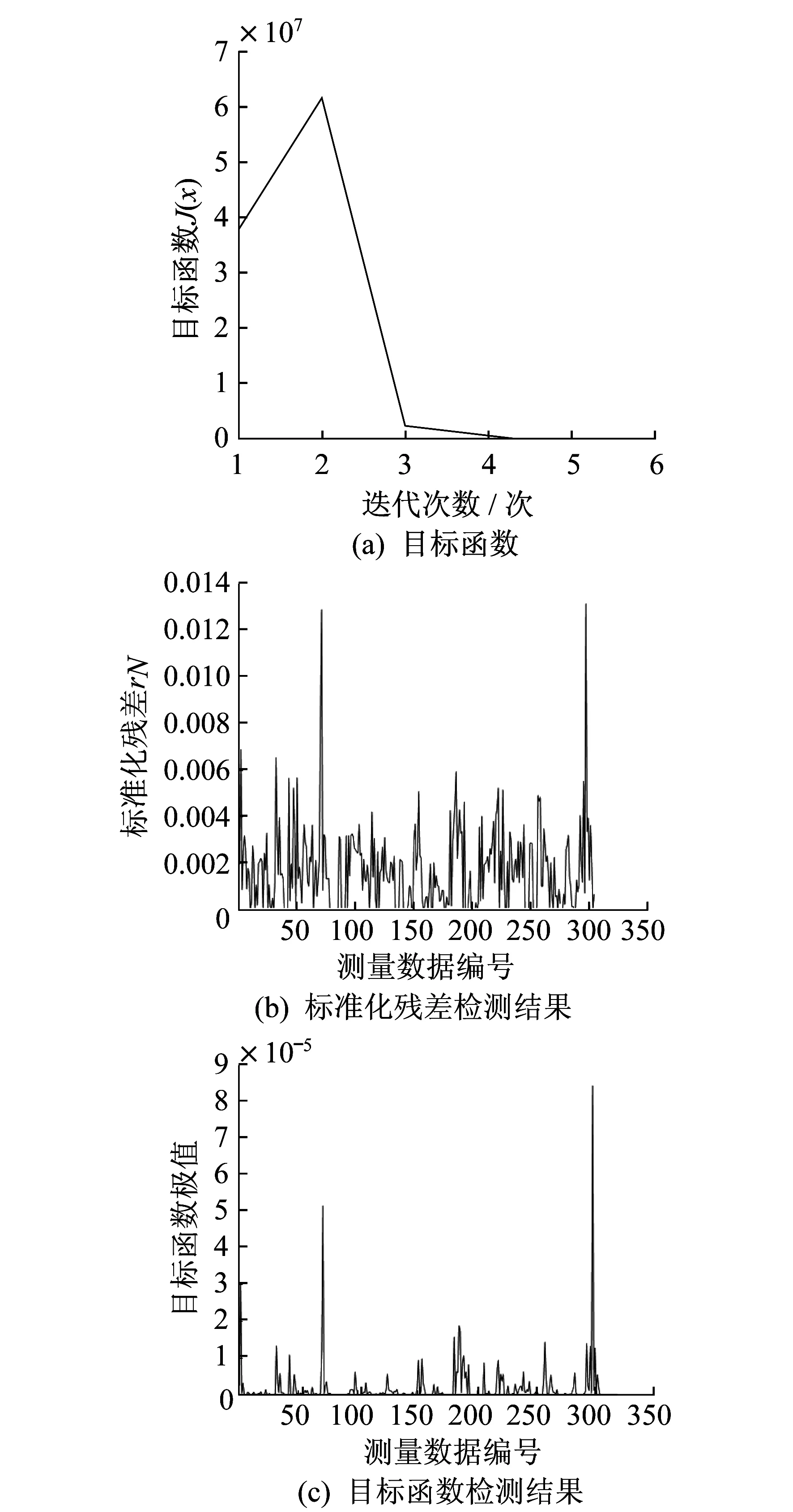
图7 IEEE 118节点系统虚假数据注入下的检测结果

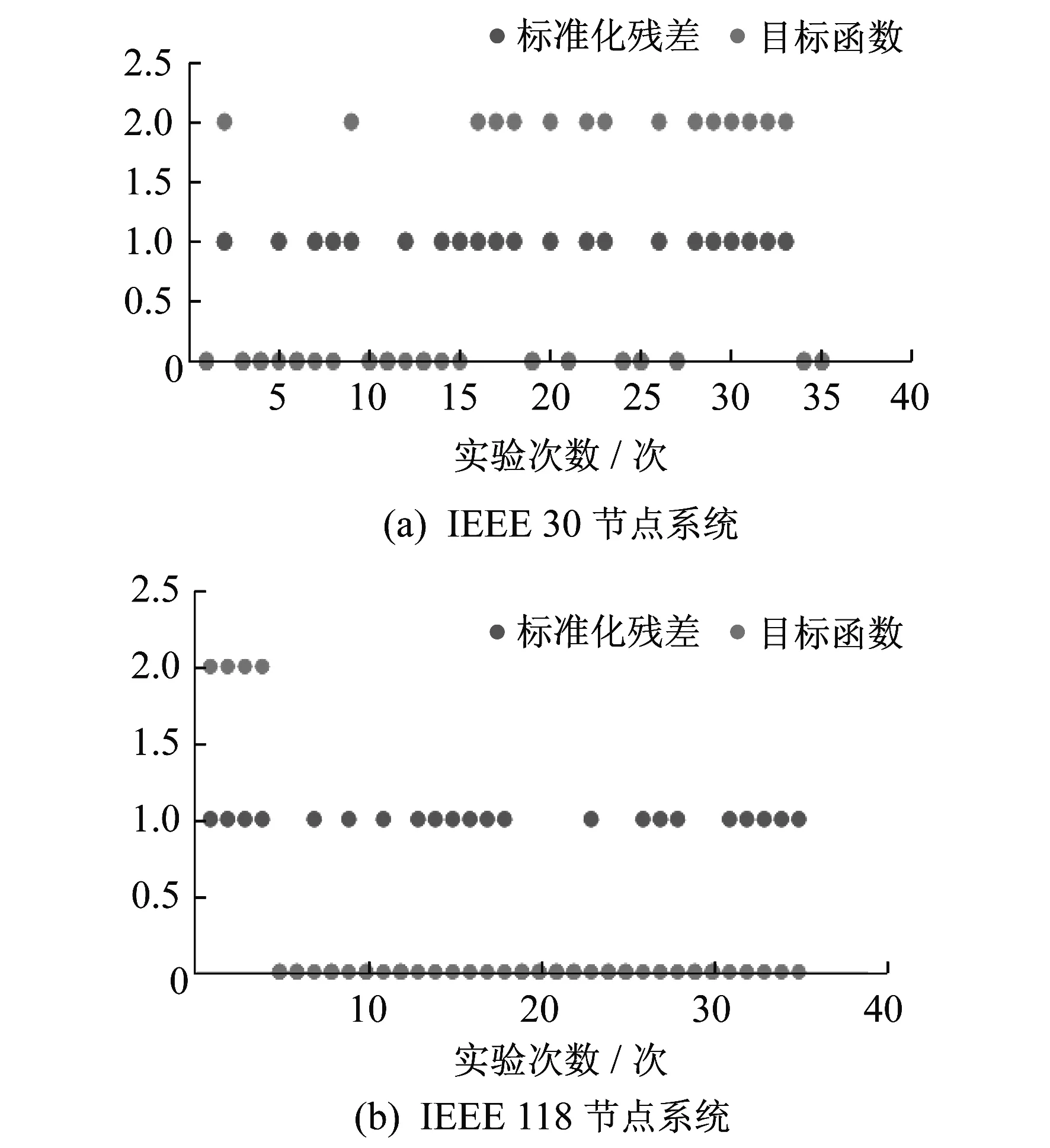
图8 两种系统中两种方法的检测结果

(15)

式中:TP——被判定为无攻击,且实际无攻击存在的情况数;

FP——被判定为有攻击存在,但实际未攻击的情况数。

误报率是系统把正常行为作为入侵攻击而进行报警的概率和把一种周知的攻击错误报告为另一种攻击的概率。

(16)

式中:FN——被判定为无攻击发生,实际却发生攻击的情况数;

TN1——被判定有攻击存在,但实际与判定的攻击不一致的次数;

TN——被判定为有攻击存在,实际也发生攻击的情况数。

漏报率指被检测网络受到入侵攻击时,系统不能正确报警的概率。通常利用已知入侵攻击的实验数据集合来测试系统的漏报率。

(17)

式中:N——总体攻击发生的次数。

采用上述3个指标对数据进行分析,结果如表1所示。

表1 结果分析 单位:%

由表1可以看出,两种针对传统恶意数据的检测方法对虚假数据注入的检测效果不好,存在较低的检测率和较高的误报率、漏报率。这说明残差检测对虚假数据注入攻击的局限性较大。

在对电力系统恶意数据的检测方面,J(x)属于总体检测,在电力系统规模较小,量测的冗余度较小时,有较高的灵敏度。rW与rN检测法不属于总体型检测法,电力系统规模不影响检测灵敏度。此外,不良数据的检测能力与量测系统中测点的配置、不良数据值的大小以及检测门槛值有关。测点配置越完善,不良数据值愈大,检测门槛值愈低,检测不良数据的能力也愈强。单数过低的门槛值又会使误检概率增大[15]。

经过反复实验证明,残差检测法通过判断测量值与量测估计值之差是否超过界限来检查,并不能适应虚假数据注入的情况。特定的攻击矢量,使残差不包含攻击矢量的影响,导致检测失败。

5 结 语

在当前的智能电网中,FDIA发生在攻击者对网络拓扑部分已知的情况下,通过构造攻击向量,篡改电力系统的状态估计值,导致电网出现故障报警,从而使电网陷入错误状态。本文在虚假数据注入理论的基础上,提出了一种电力虚假数据注入攻击的残差检测方法,可以对IEEE 30和IEEE 118节点系统拓扑结构上指定的数据节点发起任意数值的单点攻击。实验结果表明,利用传统的电力系统恶意数据检测方法,存在较大的漏检和误检风险。在虚假数据注入攻击下,基于残差的检测算法不能满足系统对准确性的要求。