基于能量的微切削最小切削厚度有限元仿真研究*

周纯江,刘建成,金济民

(1.浙江机电职业技术学院 智能制造学院，浙江 杭州 310053；2.美国太平洋大学 计算机与工程学院,加利福尼亚州 斯托克顿 CA95211)

0 引 言

随着科学技术的不断发展,装备和产品的微型化已成为一种趋势。微细加工技术在生物、医学、航天、微电子等领域得到广泛的应用。其中，微细切削加工技术能有效实现复杂微型3D形状零件加工，并适应于多种材料，且具有高效率、高柔性的特点，成为了一个很有发展潜力的现代化加工技术[1，2]。

由于尺度效应、最小切削厚度、金属晶相结构等一系列新问题的产生，使得微细切削加工技术在加工机理上与传统切削技术存在较大的差异，其中最小切削厚度是微细加工中影响切削力、刀具磨损、表面质量和加工稳定性的重要因素[3]。近年来，对微细切削加工的最小切削厚度的相关研究主要集中在其形成机理、影响因素、预测模型及其对切削性能如切削力、表面质量和切削稳定性等方面[4，5]。其研究方法主要有：根据刀具几何形状及工件材料性能来建立理论预报模型、利用有限元仿真及切削试验等；通过上述方法，形成最小切削厚度与刀具圆弧半径、摩擦系数(摩擦角)、切削速度和材料切削特征定性与定量的关系。

本文将从切削能量的角度出发，对微切削过程中刀具圆弧半径上分流点的位置进行分析，提出建立在分流角与摩擦角关系上的最小切削厚度理论计算公式，通过有限元仿真对工件与刀具圆弧半径接触处的单元能量进行分析，通过最小内能的位置对最小切削厚度进行估算。

1 最小切削厚度模型的建立

1.1 分流点的形成

在微细机械加工中，由于所采用的切削厚度较小，往往只有1 μm～10 μm，甚至小于1 μm，而切削刀具受刀具的加工工艺水平所限和微细加工加工性能的要求，刀具切削刃存在一定的圆弧半径，如目前硬质合金微细铣刀都存在约2 μm左右的圆弧半径。因此，当实际切削厚度远小于刀具圆弧半径时，切削无法真正形成，刀具只是在工件表面产生挤压，形成犁切；当实际切削厚度达到某一值时，工件材料在某一点上断裂，并形成切屑，此时的切削厚度即为工件的最小切削厚度，该断裂点称为分流点。

具有刀具圆弧半径的微切削如图1所示。

图1 具有刀具圆弧半径的微切削

根据前述分析可得，可通过确定分流点的位置来得到微切削加工的最小切削厚度。对于分流点来说，分流点A以上的材料受到剪切变形形成切屑从刀具前刀面流出，A点以下的材料受到挤压形成已加工表面；A点是工件材料断裂的分界点，从能量的角度来分析，相对其它点来说，其切削所需要的能量最小，也即刀具上的A点所做的功最小。因此，可以对刀具上A点所做的功求导到0来确定A点的位置。

1.2 分流点的受力分析

当微切削加工切削厚度大于最小切削厚度时，刀具上的质点所做的功导致分流点A点上部的材料发生剪切变形，A点下部的材料发生挤压变形。A点沿切削方面的切削力Fc包含了挤压变形的切削力分量Fcp和剪切变形的分量Fcs。

当微切削处于单纯的挤压变形时，切削刃上分流点A受力情况如图2所示。

图2 微切削下切削刃上分流点A受力情况

其中，分流点A以下微元体的挤压变形在切削方向的切削力为:

dFcp=karesinθdθ+ukarecosθdθ

(1)

式中：k—切削力系数，N/mm2；a—切削宽度，mm；re—刀具圆弧半径，mm；u—粘附摩擦系数。

当切削产生剪切变形时，在切削方向产生的切削力为[6]：

(2)

式中：τs—剪切应力，Pa；φ—剪切角；γe—有效前角；β—剪切变形时工件与前刀面的摩擦角。

由于γe=θ-(π/2)，式(2)又可写为：

(3)

(4)

式中：θa—分流点位置所在的分流角；θin—刀具圆弧半径与工件接触的起始角，一般可取0；θout—刀具圆弧半径与工件接触的终止角，θout=arccos(1-(h/re))。

微切削刀具加工工件时，外力对材料做功，即对材料内部输入能量；当内部局部薄弱环节能量积累到一定值时，开始损耗大量能量，并导致产生断裂；消耗的能量与断裂有着直接对应的关系，而工件材料断裂处的能量损耗是最小的。

根据最小能量的原理，分流点应为使切削材料分离消耗功最小的地方，即有[7]：

dW/dθa=dFeS/dθa=0

(5)

将式(4)代入，经计算可得:

(6)

要使上式为0，则满足θa≈β。

因此，根据分流点使材料分离所消耗功最小所推知，分流角应近似于剪切变形时工件与前刀面的摩擦角。根据图1所示几何关系，可得最小切削厚度hm为：

hm=re(1-cosβ)

(7)

2 有限元仿真

微切削过程是一个具有尺度效应的复杂热一力耦合动态物理过程，涉及复杂的非线性问题，很难采用解析方法进行分析。而采用有限元仿真方法则可以对切削过程进行定量的分析。ABAQUS有限元仿真软件中包含丰富的、可模拟任意几何形状的单元库，具有丰富的网格类型，仿真精度高，用户不受限于预设的软件控制优点。

本文利用ABAQUS有限元仿真软件，对WC硬质合金刀具微切削Ti6AI4V及Inconel718两种工件材料进行有限元仿真，并基于上述的理论分析，从能量的角度探索微切削加工中最小切削厚度。

2.1 切削模型

微切削的正交切削有限元模型如图3所示。

图3 正交切削有限元模型

其切削的工艺参数参考实际切削中的槽铣微切削加工，刀具直径400 μm，转速50 000 r/min，切削深度为50 μm；刀具材料为WC硬质合金，前角10°,后角5°；刀具刃口圆弧半径为2 μm，仿真工件尺寸为60 μm×40 μm。仿真时刀具运动，工件静止。刀具网格采用CPE3T，工件网格采用CPE4RT，采用ABAQUS中的ALE网格自适应技术，以确保刀尖与工件接触部分的各积分单元材料稳定流动。

工件与刀具材料的性能参数如表1所示。

表1 工件与刀具材料性能参数

2.2 工件材料本构模型

材料本构方程描述了材料变形过程中的热—力学行为，是确保切削加工过程仿真准确性的基础。其中，Johnson-Cook本构模型考虑了材料的高应变、应变率及温度的综合效应，广泛应用于大应变率下黑色金属和有色金属的切削加工仿真，其具体表达式为：

(8)

二种工件材料的Johnson-Cook参数如表2所示。

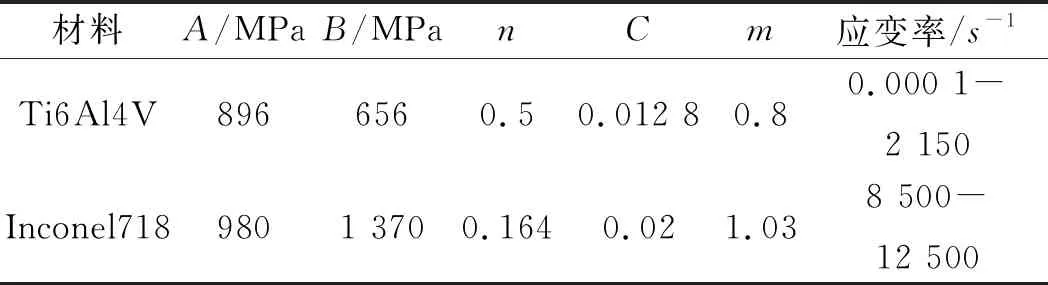
表2 工件材料Johnson-Cook参数

3 仿真结果分析

3.1 ABAQUS中的能量输出

ABAQUS有限元仿真可以通过在分析步中设置场输出变量和历史变量，来反映切削加工中工件和刀具的应力、应变、温度、位移、能量等。根据上面的分析，该例中的有限元分析通过分析仿真所得的工件能量分布，来揭示微切削最小切削厚度的规律。如前所述，刀具与工件接触部分产生断裂处的能量消耗应是最小的。因此，通过分析微加工仿真时刀具与工件接触面上的能量消耗分布可以判断加工断裂处的位置，从而判断出工件材料微加工的最小切削厚度。

在ABAQUS中，能量守恒依然遵守热力学第一定律，即：

Eu+Ek+Ef=Eqb+constant

(9)

式中：Eu—内能；Ek—动能；Ef—模型接触摩擦耗能；Ew—外部荷载作功；Eqb—周边媒介阻尼耗能。

对于该例微切削仿真工件而言，其动能为0，接触摩擦耗能在刀具与工件接触部分是一致的，刀具通过接触部分对工件做功，周边媒介阻尼耗能可以忽略。由于切削仿真是稳态的，工件材料是塑性材料，外力所做的功几乎等于系统内部的能量。因此，刀具与工件接触部分的能量分布差异主要体现在接触部分各积分单元的内能上，即：

Eu=Es+Ep+Ec+Ev

(10)

式中：Es—弹性应变能，ABAQUS中以ELSE表示整个单元的弹性应变能，其包含了损伤耗能Ed和可恢复能Ee；Ep—塑性能ELPD；Ec—时间相关量耗能，如蠕变ELCD；Ev—阻尼耗能ELVD，包括粘滞阻尼、材料阻尼。

通过ABAQUS仿真得到的刀具与工件接触面各内能云图如图4所示。

图4 刀具与工件接触面的各内能云图

从图4可以看出：在稳态微切削塑性材料时，刀具与工件接触面的各单元上蠕变能耗ELCD等于0，阻尼耗能ELVD的最大值约2×10-7，弹性应变能ELSE最大值约1.7×10-7左右，且在刀具与工件的接触面上分布比较一致，而塑性能ELPD的最小值为3.6×10-6；相对于塑性能ELPD而言，弹性应变能ELSE和阻尼耗能ELVD在单元内能中的占比较小，可忽略不计；接触面各单元的塑性能ELPD代表了单元总内能值，可以通过分析接触面各单元的最小塑性能ELPD，来判断微切削工件时工件材料最小能量处，即发生断裂的位置，从而确定在当前切削条件下工件材料的最小切削厚度。

3.2 结果分析

3.2.1 最小切削厚度的存在

以上通过仿真模拟证实了在微切削加工过程中存在最小切削厚度。当加工的切削厚度小于最小切削厚度时，工件不产生切削，只对加工表面进行挤压。

切削厚度较小时微加工仿真应力云图如图5所示。

当这两种工件材料切削厚度为0.3 μm时，整个切削过程不产生切屑，刀具从切入工件开始，一直到仿真设定的时间结束，工件表面只受到刀具的挤压，不产生实际的切削。

图5 切削厚度较小时微加工仿真应力云图

3.2.2 刀具与工件接触面上的最小内能

当加工的切削厚度超过最小切削厚度时，工件产生切削并形成切屑，其中在分流点上部形成切屑，分流点处材料发生断裂，断裂处的材料内部能量在刀具与工件接触面上最小。通过ABAQUS仿真所得工件与刀具接触部分的内能主要是塑性能，且塑性能较小部分并非集中于一点，而是有一个一定宽度的区域。这与相关文献所得到的结论较为一致[8]。

刀具刃口圆弧半径为2 μm，切削材料为Ti6Al4V和Inconel718，切削厚度为1 μm和1.5 μm时，各单元的塑性能ELPD云图如图6所示。

图6 ABAQUS仿真塑性能ELPD云图

从图6中可以看出：工件在切削时已形成实际的切屑在刀具切入工件一段时间后，在刀具与工件的接触面上始终存在一个区域，这个区域内的塑性能ELPD最小，在某些时候甚至接近于0；区域两侧的塑性能沿接触面增大，随着切削的不断进行，最小能量区域的网格不断缩小，直至网格被删除，形成实际的切屑。

笔者运用ABAQUS中的路径显示功能，对材料Ti6Al4V切削厚度1.5 μm的仿真结果设置相应的显示路径，在刀具与工件接触面上显示各单元的ELPD分布值；其中，Y坐标为设置的起点与各后续点的Y向距离，X为各单元积点上的ELPD分布值，具体如图7所示。

由图7可知，由于路径的初始点是刀具的Y向最低点，因此可根据能量最小区域的Y值来判断工件的最小切削厚度；在同样的切削条件下，同一种材料这一区域的位置基本保持不变，不同材料的这一区域的位置有所不同。

图7 仿真显示路径设置及ELPD能量值(材料Ti6Al4V切削厚度1.5 μm f 0.3)

3.2.3 最小切削厚度与摩擦角的相关性

工件材料的分流点的位置，即最小切削厚度值的大小与刀具与工件材料接触时的摩擦系数直接相关，摩擦系数越大，则工件的最小切削厚度也越大。但是摩擦系数并非决定工件的最小切削厚度唯一因素，并非理论分析中的分流角等于摩擦角。

如工件材料Ti6Al4，切削厚度1.5 μm，仿真时取刀具与工件材料的摩擦系数为0.5时，其ELPD能量云图和PATH路径上各点的能量值如图8所示。

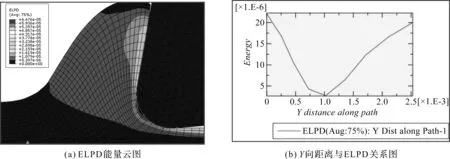
图8 ELPD云图及路径能量值(材料Ti6Al4，切削厚度1.5 μm，f 0.5)

通过PATH路径上各点的能量值显示，最小能量值处的Y向距离值与图7(b)相比有明显的增加，即最小切削厚度值比摩擦系数为0.3时有所增大。以摩擦系数0.5为例，可推出摩擦角为26.56°，根据式(7)，则hm=0.11re,这与仿真所得结果和相关文献研究结论有较大的差值。这是由于通常所设定的摩擦系数是指工件材料与前刀面的摩擦，而微细加工中由于刀具圆弧半径与加工实际厚度往往在一个数量级上，其摩擦机理远比通常的前刀面摩擦复杂，前刀面摩擦系数是影响最小切削厚度的重要因素。

不同材料取同样的摩擦系数得到的最小切削厚度也是不同的，最小切削厚度与工件材料自身的切削性能参数有关。通过仿真显示，微加工Ti6Al4V和Inconel718两种材料，采取WC硬质合金切削，摩擦系数取为0.3时的最小切削厚度分别为0.2R和0.25R，仿真结果与相关文献研究所得较为一致[9]。

4 结束语

由于微细切削加工中存在最小切削厚度，且以材料切削时的分流点为界，分流点上部材料产生剪切变形，下部材料为挤压变形；通过最小能量法，笔者对微切削加工中工件材料在一定切削条件下的最小切削厚度进行了估算，通过运用ABAQUS仿真软件，对工件与刀具圆弧半径接触处的单元能量进行了有限元仿真。

研究结果表明：理论上的分流点在仿真中显示为具有相对较小能量值的较小区域；刀具与工件的摩擦系数是影响最小切削厚度的重要因素，且摩擦系数越大，最小切削厚度也越大，但摩擦系数不是影响最小切

削厚度的唯一因素，不同工件材料的最小切削厚度不同；通过分流区域的位置可以对一定加工条件下的最小切削厚度进行估算。