基于VMD和GWO-SVR的电力负荷预测方法

刘辉 李侯君 刘雨薇 邹琪骁

摘  要： 预测负荷的精准度是衡量电力系统负荷预测模型性能的一个重要指标。电力负荷序列变化规律多样，具有周期性、非平稳性、随机性等特点，因此采用变分模态分解方法分解负荷序列，得出其不同特性的模态函数分量，进而降低原始数据的复杂程度和模态混叠现象以提高负荷预测的精度，将其代入灰狼优化的支持向量回归机模型，得到最终日负荷预测值。使用VMD?GWO?SVR预测方法在Matlab R2014b软件上对2014年南美某地区日负荷数据进行仿真验证，结果表明该方法使得日负荷预测精度可达99.15%，验证了该预测模型的有效性和高精度。

关键词： 负荷预测; 变分模态分解; 灰狼优化算法; 支持向量机; 预测精度; 周期性

中图分类号： TN99?34; TM715                    文献标识码： A                      文章编号： 1004?373X（2020）23?0167?06

Abstract： The accuracy of load prediction is an important indicator to estimate performances of a power system load forecasting model. The power load sequence has various variation rules， such as periodicity， non?stationary and randomness. Therefore， the VMD （variational mode decomposition） method is used to decompose the load sequence and obtain the modal function components with different characteristics， so as to reduce both the complexity of the original data and the modal aliasing to improve the accuracy of load forecasting， and put it into the grey wolf optimized SVR （support vector regression） machine model to obtain the final daily load forecasting value. In this paper， the prediction method of VMD?GWO （grey wolf optimizer）?SVR is used to simulate the daily load data of a region in South America by the software Matlab R2014b. The results show that the method realizes an accuracy of daily load forecast of 99.15%， which verifies the high precision of the prediction model.

Keywords： load forecasting; VMD; GWO; support vector machine; prediction accuracy; periodicity

0  引  言

准确的电力负荷预测有助于保证电力系统安全经济运行，是实现电网智能化管理和电力生产优化调度的重要依据，同时也是智能电网建设的关键一环[1]。电力负荷预测可以帮助电网公司为各类用户提供可靠的电能，对安排电厂发电量及停电检修计划提供重要信息，从而保证电网运行的安全稳定性和社会的正常生活需要，有效地减少突发性停电带来的重大经济损失。对于如何提高电力系统用电负荷预测的精度是当前电力系统重要的研究方向之一 [2]。

负荷预测大体可分为传统方法和人工智能算法两类，传统预测方法有趋势外推法、回归分析法、灰色模型法。随着人工智能算法的不断发展，神经网络、小波分析以及支持向量机[3]（Support Vector Machines，SVM）等算法渐渐广泛应用于负荷预测上。

文献[4]将电力负荷序列运用EMD分解为若干个独立IMF和余项，再将其代入PSO?SVM算法建立中期负荷预测模型，此方法揭示了负荷变化特性和环境因素影响。文献[5]运用BP神经网络进行负荷预测，BP网络结构简单，具有较好的自学习、自适应能力，但初始阈值和权值的选择对网络训练的速度和精度影响程度较大，该算法还存在许多不足。文献[6]采用支持向量机算法对影响预测结果的特征进行预测，并通过实例仿真验证了模型具有较强的泛化能力，但对于较大负荷数据预测时，会消耗大量内存空间、计算时间较长。

由于EMD分解易造成模态混叠现象，为提高预测精度，本文采用变分模态分解（Variational Mode Decomposition，VMD）算法进行改进，VMD具有良好的鲁棒性，且通过收敛条件的合理控制，其分量个数也远小于EMD和EEMD。采用SVM进行预测，克服了神经网络易陷入局部最优解、运算时间长等常见问题，该方法被当作是神经网络的替代方法，在电力负荷预测等领域得到了广泛应用。支持向量回归机的预测精度主要取决于其参数，利用遗传优化算法、蝙蝠优化算法和人工鱼群算法等优化智能算法对参数寻优极大提高了模型的预测精度。因此本文采用灰狼优化（Grey Wolf Optimizer，GWO）算法优化SVR参数，提高预测精度。

1  VMD原理

对于非线性、非平稳信号，VMD算法能有效提取特征信息。该算法主要由变分问题的构造、求解两部分构成，原理是利用每个模态都存在着中心频率带宽，在保证模态分量的带宽之和最小时，将信号分解成[k]个分量[7?8]。

4） 判别精度为[ε>0]，若满足[kun+1k-unk22unk22<ε]条件，则算法停止，否则将返回步骤2）进行运算。

2  GWO的SVR模型

2.1  GWO算法

Mirjalili等人在2014年提出一种基于群体的启发式算法——GWO算法，该算法模仿了自然界中灰狼捕食猎物行为，通过分工、游走、包围、猎杀和攻击等行为优化目标问题。GWO算法包含内容如下[9?10]：

1） 社会等级

在自然界中灰狼群体处于食物链的顶端，有着严格的等级制度。种群分为4个阶级：第一阶级为狼[α]，主要工作是负责对狩猎行为作出决策;第二阶级为狼[β]，头狼[α]缺失时，[β]接替[α]做出决策;第三阶级为狼[δ]，为第三决策者，遵循[α]和[β]的指令行动;最底层的狼[ω]为一般成员。前三阶级适应度从高到低依次排列，引导狼[ω]对目标范围进行搜索。

2） 包围猎物

4） 攻击猎物

狩猎完成的标志是猎物停止移动，这一过程可以通过降低[a]来实现。随机值[A]代表狼群是猎杀还是寻找新位置。当[A<1]时，表示狼强制攻击猎物。

5） 寻找猎物

灰狼群体有着分头搜索猎物的习性，同时，基于[α]，[β]和[δ]的位置猎杀猎物，当[A>1]时，灰狼远离猎物，[A<1]时灰狼强制进行狩猎，当终止条件满足时，灰狼算法迭代停止。

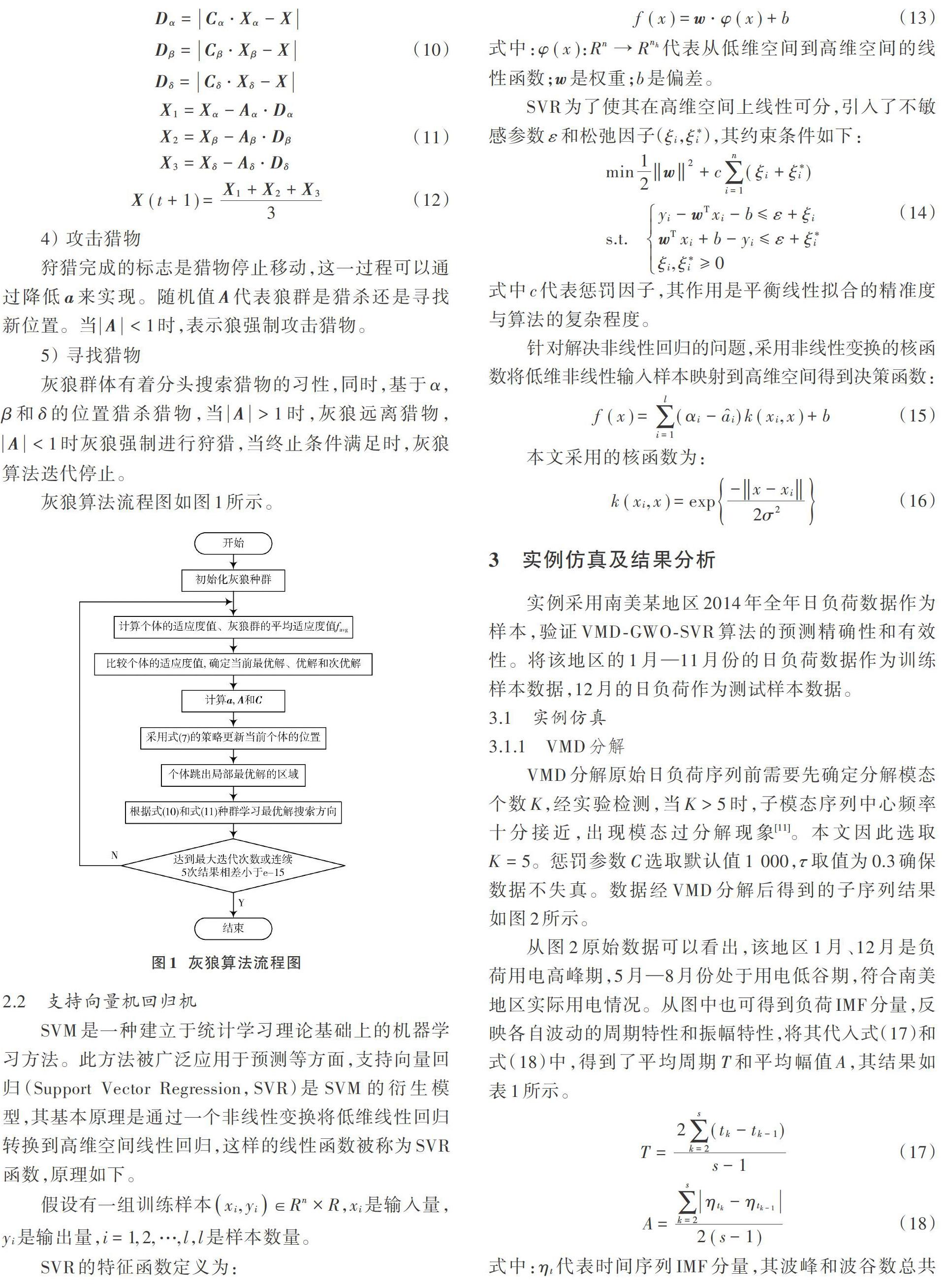
灰狼算法流程图如图1所示。

2.2  支持向量机回归机

SVM是一种建立于统计学习理论基础上的机器学习方法。此方法被广泛应用于预测等方面，支持向量回归（Support Vector Regression，SVR）是SVM的衍生模型，其基本原理是通过一个非线性变换将低维线性回归转换到高维空间线性回归，这样的线性函数被称为SVR函数，原理如下。

3  实例仿真及结果分析

实例采用南美某地区2014年全年日负荷数据作为样本，验证VMD?GWO?SVR算法的预测精确性和有效性。将该地区的1月—11月份的日负荷数据作为训练样本数据，12月的日負荷作为测试样本数据。

3.1  实例仿真

3.1.1  VMD分解

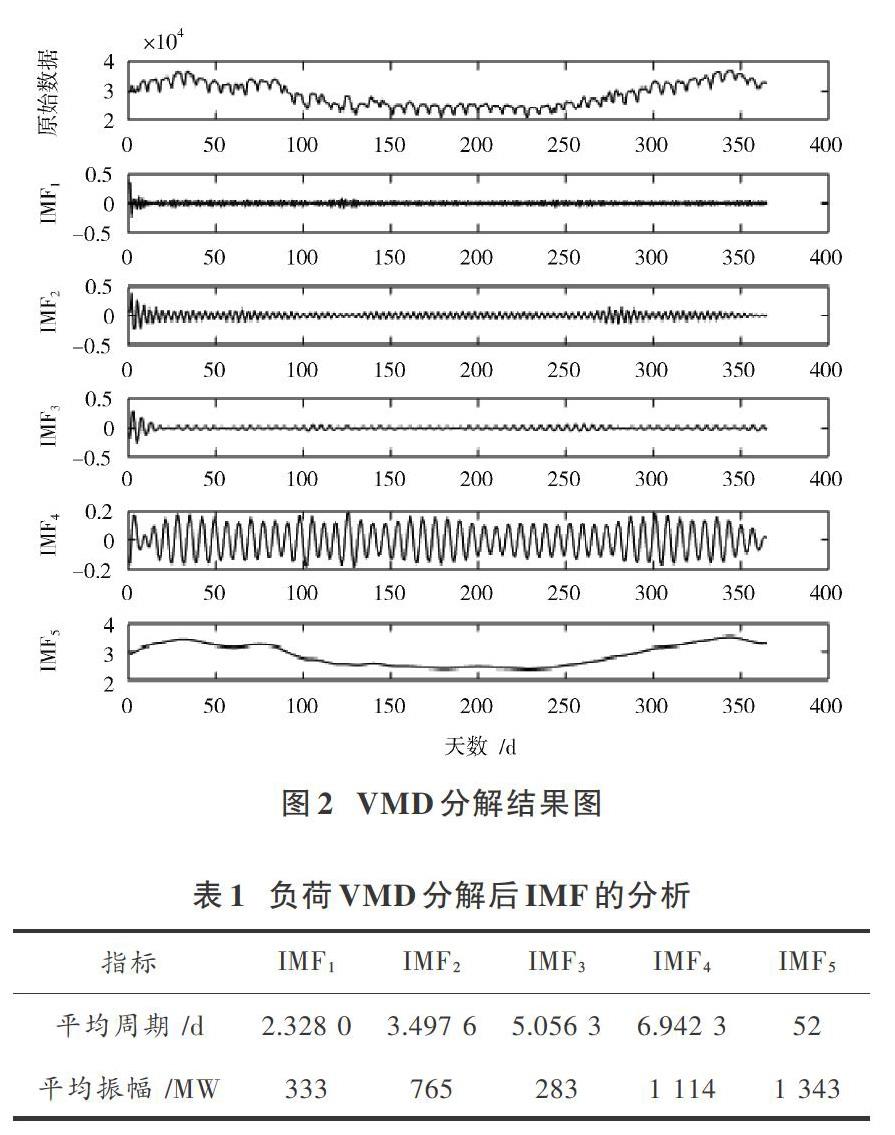
VMD分解原始日负荷序列前需要先确定分解模态个数[K]，经实验检测，当[K>5]时，子模态序列中心频率十分接近，出现模态过分解现象[11]。本文因此选取[K=5]。惩罚参数[C]选取默认值1 000，[τ]取值为0.3确保数据不失真。数据经VMD分解后得到的子序列结果如图2所示。

从图2原始数据可以看出，该地区1月、12月是负荷用电高峰期，5月—8月份处于用电低谷期，符合南美地区实际用电情况。从图中也可得到负荷IMF分量，反映各自波动的周期特性和振幅特性，将其代入式（17）和式（18）中，得到了平均周期[T]和平均幅值[A]，其结果如表1所示。

从表1可知，[IMF]分量周期性明显，但不是单纯以7天为一个周期的时标特性，说明总负荷周期是由多重负荷周期规律相交织而成，会受到多种因素的周期结果影响，而IMF5低频分量的电力负荷平均幅值最大，表明对负荷的贡献程度大，如果其预测错误，会导致整体预测精度下降。

3.1.2  负荷预测流程

1） 提取历史日负荷数据，由VMD原理式（3）～式（5）可分解得到IMF1，IMF2，…，IMF5;

2） 将1月—11月分解的IMF1，IMF2，…，IMF5作为训练集，12月份分解的IMF1，IMF2，…，IMF5作为预测集;

3） 将训练集代入GWO?SVR模型进行训练;

4） 将预测集代入训练后的模型，从而得到日负荷预测结果。负荷预测流程图如图3所示。

3.2  结果分析

3.2.1  有效性

为了验证本文基于VMD?GWO?SVR算法的有效性，将该预测方法与采用优化前的支持向量机预测法、VMD?BP神经网络预测法、VMD?SVR预测法和实际日负荷进行对比，其结果如图4所示。

从图4可以看出，本文改进算法相比其他3种预测方法，与实际日负荷曲线拟合程度更好。通过VMD?SVR预测法与SVR预测法的曲线对比，证明了对变分模态分解的信号进行预测确实有效;再对比VMD?BP预测法、VMD?SVR预测法和VMD?GWO?SVR预测法的拟合曲线，验证了VMD?GWO?SVR预测法的有效性。

3.2.2  精确性

由于相对误差可以有效体现出预测方法的精确性，将VMD?GWO?SVR预测法与其他3种预测方法的相对误差相比，对比结果如图5所示。

从图5中可知，每个预测样本间相对误差都显著降低，反映了该方法预测效果具有较高的精确性。

为了进一步体现VMD?GWO?SVR算法的精确性，将从均方误差（MSE）、平均相对误差（MAPE）、平均绝对误差（MAE）和最大误差（MW）4个指标来衡量，并单独用表2列出2014年12月份实际负荷数据和预测数据使预测结果更为直观。

表2为4种预测方法分别对2014年12月份实际电力负荷值的预测结果。从其中可以得出：数据在没有经过VMD分解处理时，其预测结果与实际负荷值之间误差较大。在经过VMD处理数据的3种算法中（VMD?BP，VMD?SVR，VMD?GWO?SVR），VMD?GWO?SVR预测方法的预测结果与实际值相差较小。从表3的预测结果误差对比分析中可以得出4种算法的平均相对误差分别为1.26%，1.23%，1.14%，0.85%。结果表明用VMD分解后的数据进行预测，其平均相对误差都小于SVR算法的相对误差预测结果。对数据进行VMD分解可以有效减小预测方法的相对误差，提高预测方法的精度，且数据在经过VMD分解后，使用GWO优化的SVR算法，即本文所提出的VMD?GWO?SVR预测算法，其预测的平均相对误差可以减小0.29%，所以对经过VMD处理后的数据再进行GWO优化处理可以更进一步地减小平均相对误差值，这种预测方法有效平衡探索和局部寻优之间的矛盾，避免了目标陷入局部最优解与收敛速度过快的问题。因此对历史负荷序列进行变分模态分解能从中提取更多的有效信息，再经过GWO优化的SVR对分解的数据进行数学建模，可进一步减小平均相对误差，验证了该方法的精确性。

4  结  语

本文提出了一种基于VMD和GWO?SVR参数的预测算法，用于对日电力负荷进行预测。用VMD分解算法可知日电力负荷受多种因素的周期性影响，其中受[IMF5]分量因素影响最为明显，其值不精确会使预测值产生较大误差。SVM算法在预测方面得到了广泛的应用，但由于运算速度慢，本文采用了GWO优化SVR参数，使其运算速度更快，其结果也更加精确，在南美某地区的日负荷数据中得到了验证。将VMD分解的周期性数据代入GWO?SVR模型中得到预测数据，通过4种评价指标评估，表明该方法相较于其他算法预测结果更加精确，平均相对误差减小0.41%，为负荷预测提供了新思路。

参考文献

[1] 王伟，杨辉华，刘振丙，等.基于极限学习机的短期电力负荷预测[J].计算机仿真，2014，31（4）：137?141.

[2] 王吉权，王福林，董志贵，等.基于改进BP神经网络的电力负荷预测[J].数学的实践与认识，2017，47（9）：276?284.

[3] 程启明，陈路，程尹曼，等.基于EEMD和LS?SVM模型的风电功率短期预测方法[J].电力自动化设备，2018，38（5）：27?35.

[4] 田淑慧.基于经验模态分解的IPSO?SVM风电功率预测[D].株洲：湖南工业大学，2018.

[5] 孟凡喜，屈鸿，侯孟书.基于GA和SVM的电力负荷预测方法研究[J].计算机科学，2014，41（z1）：91?93.

[6] 宋娟，潘欢.基于果蝇算法和SVM的天然气日负荷预测[J].控制工程，2017，24（10）：1995?2002.

[7] 胡欣球，马立新.VMD?LSTM算法在短期负荷预测中的应用[J].电力科学与工程，2018，34（6）：9?13.

[8] NIU Mingfei， HU Yuerong， SUN Shaolong， et al. A novel hybrid decomposition?ensemble model based on VMD and HGWO for container throughput forecasting [J]. Applied mathematical modeling， 2018， 57： 163?178.

[9] 徐達宇，丁帅.改进GWO优化SVM的云计算资源负载短期预测研究[J].计算机工程与应用，2017，53（7）：68?73.

[10] 张涛，张东方，王凌云.基于灰狼算法的分布式电源优化配置[J].水电能源科学，2018，36（4）：204?207.

[11] XIE Xiaomin， WANG Tingting. A projection twin SVM?based active contour model for image segmentation [C]// International Conference on Mechatronics & Machine Vision in Practice. Nanjing， China： IEEE， 2017： 1?4.

[12] XIAO Yancai， KANG Na， HONG Yi， et al. Misalignment fault diagnosis of DFWT based on IEMD energy entropy and PSO?SVM [J]. Entropy， 2017， 19（1）： 6.

[13] YI Liyan， HAN Dong， YAN Zheng. Long?term system load forecasting based on data?driven linear clustering method [J]. Journal of modern power systems & clean energy， 2018， 6（2）： 306?316.

[14] 孙晨，李阳，李晓戈，等.基于布谷鸟算法优化BP神经网络模型的股价预测[J].计算机应用与软件，2016（2）：276?279.

[15] 周红标，王乐，卜峰，等.基于PSO?WPESN的短期电力负荷预测方法[J].电测与仪表，2017，54（6）：113?119.