一种基于微分求积的空间分数阶扩散方程求解方法
朱晓钢, 聂玉峰
(1.邵阳学院 理学院,邵阳 422000;2.西北工业大学 应用数学系,西安 710129)
1 引 言
分数阶微积分是微积分理论的重要分支,也是经典微积分的任意阶推广,弥补了经典微积分理论在应用方面的不足。分数阶微积分的一个最为突出的特点在于能捕捉动力学行为的记忆效应,更好地反映系统函数发展的历史依赖性。近十几年,利用带分数阶导数的微分方程刻画自然界中的反常现象一直是学术界关注的焦点之一,潜在的应用已囊括各个学科领域,如电化学、金融、生物工程、材料科学和统计物理等[1-3]。
考虑变系数空间分数阶扩散方程
(1)
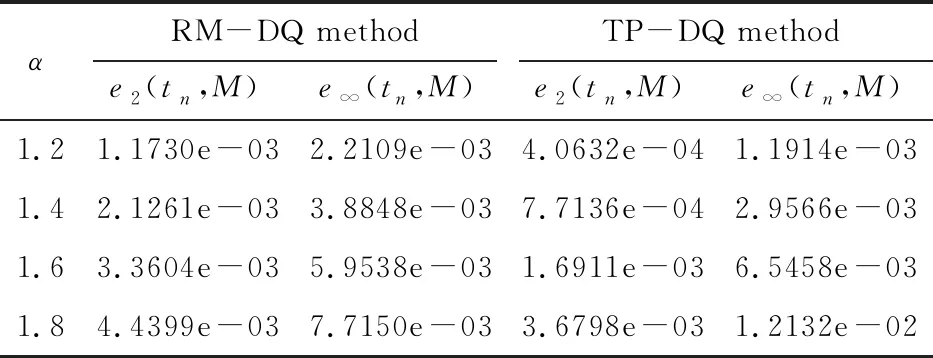
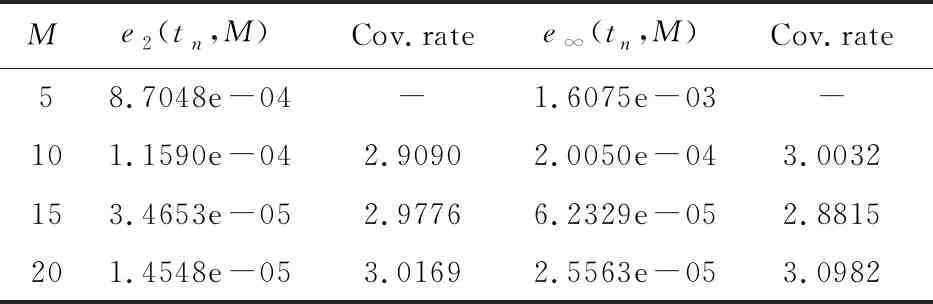
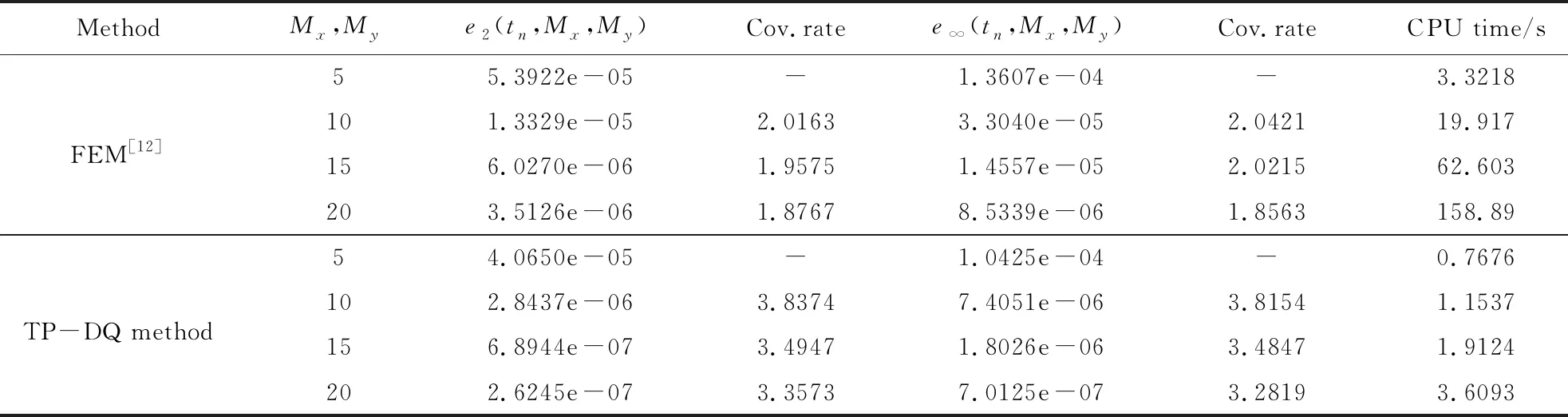
式中1 <α≤2,x∈Λ,Λ= [xL,xR],0 u(x,0) =u0(x) (x∈Λ) (2) u(xL,t) =g1(t),u(xR,t) =g2(t) (0 此处,κ(x)和υ(x)是x的非负函数且不同时恒为0,当κ(x) ≡ 0时g1(t)可不为0,当υ(x) ≡ 0时g2(t)可不为0。在式(1)中,分数阶导数的定义为 (4) 式中Γ(·)为欧拉Gamma函数。 在数学物理中,空间分数阶偏微分方程(1~3)可以描述诸多现象,如反常扩散、弹性振动和波的传播等[4,5]。与整数阶偏微分方程相比,其在反映物理系统随时间演化上更具优势。由于解析技术的局限性,数值方法越来越受到人们的重视,并且在研究中获得了广泛的应用,典型的方法包括有限差分法[6-9]、有限元法FEM[10-12]、无网格点插值法MPIM[13,14]和有限体积法[15]。Xu等[16]给出了分数阶对流扩散方程的间断Galerkin方法。Ilic等[17,18]基于导数的矩阵表示提出了矩阵转换法。文献[19]讨论了一种稳定的方向分裂谱Galerkin方法;文献[20]构造了求解变系数空间分数阶扩散方程的径向基配置法。Ford等[21]将Riemann-Liouville 导数转化成等价的Hadamard有限部分积分,并运用分段二次多项式对被积函数插值建立了一种新的有效方法。Li等[22]研究了二维非线性空间分数阶扩散方程的时空勒让德谱配置法。 由于分数阶导数的非局部性质,采用常规数值方法求解空间分数阶问题通常面临着算法复杂、计算量大和效率低等困难,因此寻找一种简便高效的算法非常必要。微分求积法(DQ Method)是求解微分方程的高效数值方法,其基本思想是利用函数值的加权线性组合替换导数,将微分方程转化成方程组[23],试函数可选择正交多项式、径向基函数、样条和拉格朗日插值多项式[24-26]。 该方法具有计算量小、对维数增长不敏感和易于编程实现等特性。鉴于此,本文将微分求积法推广到方程组(1~3)及与之对应的高维空间分数阶问题,介绍分数阶导数的微分求积公式,利用Reciprocal Multiquadrics和Thin-Plate Splines两种径向基函数作为试函数确定加权系数,形成的常微分方程组采用Crank-Nicolson格式离散。最后,数值算例的数值结果及与现有算法的比较展示了其在计算精度和计算效率上的优势。 回顾分数阶导数的定义、基本性质及与径向基函数方法相关的一些辅助结论。 设α∈+和Λ= [a,b],那么 (5) (6) 分别是α-阶左Caputo和右Caputo分数阶导数的定义,此处,f(x) ∈Cm(Λ),当α∉时,m=[α]+1,反之,当α∈时,m=α,[ · ]是向下取整函数。α-阶左Riemann-Liouville和右Riemann-Liouville分数阶导数的定义分别是 (7) (8) (9) (10) 关于分数阶导数的更多性质参见文献[3,27]。 (∀x∈Λ)(11) 式中 (i= 1,2,…,mp)(13) 考虑两种类型的径向基函数,即 Reciprocal Multiquadrics: Thin-Plate Splines: 式中k= 0,1,…,M,ε为形状参数。对于Reciprocal Multiquadric径向基函数,由式(11~13)生成的插值矩阵是严格正定的,即使在无多项式项P(x)时也一样;而对于Thin-Plate Spline径向基函数,插值矩阵却是条件正定的,需满足mp≥2。所以,在采用径向基插值构造数值方法时,P(x)对于Thin-Plate Spline径向基函数是不可或缺[28]的。 介绍分数阶导数的微分求积公式,基于Reciprocal Multiquadric和Thin-Plate Spline径向基函数,给出计算加权系数的方法。在[xL,xR]上定义xL=x0 (i,k= 0,1,…,M)(14) (i,k= 0,1,…,M)(15) (16) (17) 情况I Reciprocal Multiquadrics当mp= 0时,由于式(11~13)生成的代数问题是唯一可解的,因此,该情况的加权系数的计算公式可直接通过替换式(14,15)的基函数获得,即 (i,k= 0,1,…,M)(18) (i,k= 0,1,…,M)(19) 针对节点xi,将式(18,19)整理成矩阵形式为 (20) 情况II Thin-Plate Splines由于Thin-Plate Spline径向基函数是条件正定,为了保证代数问题的适定性,需加上多项式项P(x)。为简便起见,本文取mp= 2,根据式(11~13),有 (∀x∈Λ)(21) (22) 利用式(22)消去式(21)的变量λ0(t) 和λ1(t),可知 (23) 再通过式(14~17),得到 (i= 0,1,…,M)(24) (i= 0,1,…,M)(25) 此处,k= 2,3,…,M,并且 (26) 特别地,当k= 0,1,有 (27) 这是因为∂α1/∂±xα= 0和∂αx/∂±xα= 0。然后,针对每个节点xi,整理式(24~27),最终得 (28) 下面介绍Dα(· )的计算过程。一般来说,函数分数阶导数的显式表达式很难推导,这是由其弱奇异性质决定的。但通过适当的积分变换,可以通过数值积分公式来逼近。分别对左右Caputo分数阶导数作积分变换ξ=x-(x-xL)(1+ζ)/2和ξ=x+(xR-x)(1+ζ)/2,可以验证 (29) (30) 可以看出,式(5,6)的积分已演变成 (32) (33) 式中P∈+,且当k(x)为k(x)时,有 (34) Q(x) = (x-xi)2 σ - 2[(2σ-1)σlog(x-xi)2+ (x1-x0) (35) 通过上述微分求积公式建立求解方程组(1~3)的全离散微分求积格式。在区间[0,T]上定义等距网格节点tn=nτ(τ=T/N,N∈+)。将加权线性组合(16,17)代入式(1),得 (36) (37) 式中i= 1,2,…,M-1,以及 (38) 求解高维空间分数阶问题是一项富有挑战性的课题。将上述微分求积法推广到高维情形,由于对维数增长不敏感,采用其处理高维问题具备较大的便利性。以二维情形为例,三维情形以此类推,考虑二维空间分数阶扩散方程 (39) 式中(x,y)∈Λ,0 u(x,y,0) =u0(x,y)((x,y) ∈Λ) (40) u(x,y,t) =g(x,y,t)((x,y) ∈∂Λ,0 (41) 此处, 1 <α,β≤2,Λ= [xL,xR]×[yL,yR],∂Λ为边界,κ+(x) ,κ-(x) ,υ+(x) 和υ-(x) 是非负函数且不同时恒为0。边界条件(41)应与式(39)相容,如当κ+(x) ≠ 0时,g(x,y,t)必须在x=xL处为0;反之,如果κ-(x) ≠ 0 ,则必须在x=xR处为0。式(39)的分数阶导数的结构类似于式(5,6),如在y-轴方向的定义为 (42) 为构造二维分数阶导数的微分求积公式,在区域Λ上定义xL=x0 (43) (44) (45) (46) (k= 0,1,…,Mx) 而在y-方向,有 (k= 0,1,…,My) (47) 式中i= 1,2,…,Mx-1,j= 1,2,…,My-1,以及 通过5个数值算例来验证所提方法(分别简称RM-DQ和TP-DQ方法)的精确性和可靠性。径向基函数的分数阶导数的计算统一选择50个积分节点和权值,运用公式 (48) 来衡量误差,Mtotal= (Mx+1)(My+1),再令0<ε<1,相应的收敛速率利用 (49) 来计算,ν=2和∞。固定σ= 2,而对于Reciprocal Multiquadrics的形状参数,如何选取最优值(误差最小)仍然是一个开放性问题,有待深入研究,但通过参考文献[30-32],可选择=cdim/(M+1)0.5(c> 0,dim=,x或者y)。 (50) (x)k表示阶乘,即(x)k=x(x+1)…(x+k-1)。取c= 1.45和M= 20,不同α下的数值结果列入表1。 可知,分数阶导数的微分求积公式是有效的,在给定的参数下除α= 1.6和1.8的最大模误差外,TP-DQ方法的误差均小于RM-DQ方法。 算例2考虑空间分数阶扩散方程 f(x,t) (51) 计算区域为[0,1],施加初边值条件 u(x,0) = 10x2(1-x)2 u(xL,t) =u(xR,t) = 0 (52) 解析解为u(x,t) = 10e-tx2(1-x)2。源函数通过解析解代入式(51)获得。由于u(x,t)的一阶导数及其本身在边界点xL和xR处均为0,根据性质(9,10),Caputo和Riemann-Liouville导数等价。取α= 1.6和c= 0.68,比较有限元法[11]、无网格点插值法[14]和微分求积法在t= 0.5处的均方误差,对比结果列入表2,其中,有限元法取τ= 1/M2,无网格点插值法和微分求积法选用τ= 1/M。由 表1 算例1中M = 20时的数值结果 表2 当α= 1.6时有限元法、无网格点插值法和微分求积法在t= 0.5处的均方误差比较 表2 可知,微分求积法的精度要高于前两种方法。算例3考虑空间分数阶扩散方程 (53) 计算区域为[0,1],施加初边值条件 u(x,0) = 0,u(xL,t) = 0,u(xR,t) =t2 (54) 解析解为u(x,t) =t2x4。取α= 1.2和τ= 2.0×10-3,TP-DQ方法在t= 1处的数值结果列入表3。可以看出,TP-DQ方法在空间方向的收敛速率大于二阶;此外,即使离散节点很少,该方法也能取得令人满意的计算精度。 算例4考虑二维空间分数阶扩散方程 (55) 设Λ= [0,1]×[0,1],解析解为u(x,y,t) =e-tx2(1-x)2y2(1-y)2,初边值条件均由解析解给出,源函数通过解析解代入式(55)获得。取α=1.5,β= 1.9和τ= 2.5×10-3,同时采用文献[12]的有限元法和TP-DQ方法求解上述问题,并比较其在t= 1处的误差及计算时间,为此,有限元法使用线性元与结构化网格,对比结果列入表4。 显然,TP -DQ 方法在计算精度和收敛速率上都要高于有限元法;且在相同的参数下,微分求积法的运行时间远小于有限元法。 表3 当α= 1.2时TP-DQ方法在t= 1处的数值结果 表4 当α= 1.5和β= 1.9时有限元法和TP-DQ方法的比较Tab.4 Comparison of FEM and TP-DQ method when α= 1.5 and β= 1.9 算例5考虑三维空间分数阶扩散方程 (56) 设Λ= [0,1]×[0,1]×[0,1]和初边界条件 u(x,y,z,0) = 0,u(1,y,z,t) =t2y3z3 u(x,1,z,t) =t2x3z3,u(x,y,1,t) =t2x3y3 u(0,y,z,t) =u(x,0,z,t) =u(x,y,0,t) = 0 (57) κ+,υ+和ν+为间断系数,分别定义如下, 解析解为u(x,y,z,t) =t2x3y3z3,源函数通过解析解代入式(56)获得。取c= 1.8,α= 1.2,β= 1.3,γ= 1.5和τ= 5.0×10-3,设x-,y-和z-坐标方向的离散节点数分别为Mx,My和Mz,误差同样采用式(48)来衡量并将其分别表示成e2(tn,Mx,My,Mz)和e∞(tn,Mx,My,Mz),RM-DQ方法在t= 1处的数值结果列入表5。可以看出,RM-DQ方法的误差随着节点增多而迅速衰减且收敛速率足够高,证明本文方法适用于三维空间分数阶问题及带间断系数的空间分数阶问题。 注:上述算法,除算例2的有限元法和无网格点插值法之外,均采用Matlab R2012a编程实现,并在微机Lenovo H520上运算,配置:Intel(R) Pentium(R) G2030 3.00 GHz处理器和4 GB内存。 表5 当α= 1.2,β= 1.3和γ= 1.5时RM-DQ方法在t= 1处的数值结果Tab.5 Numerical results of RM-DQ method at t= 1 when α= 1.2,β= 1.3 and γ= 1.5 研究变系数空间分数阶扩散方程的一种全离散微分求积方法,基于Reciprocal Multiquadric和Thin-Plate Spline径向基函数,介绍了两种近似分数阶导数的微分求积公式。提出的方法具有精度高、灵活性强、无网格依赖和易于编程实现等特点。求解了5个典型问题,结果表明,在形状参数选择恰当的情况下,该方法在计算精度与效率上要优于一些现有算法。由于对维数增长不敏感,本文方法在处理高维分数阶问题上有着较大的优势。2 预备知识
2.1 分数阶导数

2.2 径向基函数方法

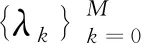
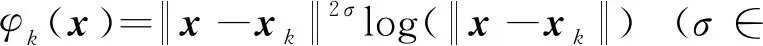
3 分数阶导数的微分求积公式
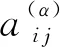
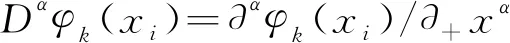
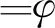
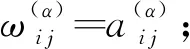


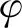
4 分数阶扩散方程的微分求积法
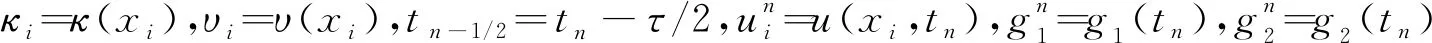
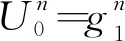
5 高维推广


6 数值算例



7 结 论

