毫米波大规模MIMO 系统中的一种低复杂度的混合波束赋形方案*

周 围，彭 洋，冉静萱，陈星宇，马茂琼

（1.重庆邮电大学，重庆 400065；2.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065）

0 引言

为解决现如今数据流量急剧增加、频谱资源紧缺等问题，第五代移动通信系统（Fifth Generation，5G）结合了毫米波和大规模多输入多输出（Multiple Input Multiple Output，MIMO）技术。一方面，毫米波可以提供更大的频带宽度，解决频谱资源紧缺的问题；另一方面，虽然毫米波在信道中传输存在较高路径损耗的问题，但毫米波的短波长特性可以减小系统中的天线尺寸，便于集成更多的天线，可结合大规模MIMO 技术克服传输路径损耗，提升通信速率。

波束赋形（Beamforming）是使电磁波在特定方向传输的技术。传统MIMO 系统中的纯数字波束赋形算法，要求每个阵元配置一条射频（Radio Frequency，RF）链。但是，在大规模MIMO 系统中，若每个阵元仍配置一条RF 链，将会造成高昂的成本和巨大的能耗。目前，研究人员为减少使用RF 链，多采用模拟/数字的混合波束赋形的架构，即模拟域只采用简单的移相器构成高维的模拟波束赋形器，而数字域采用低维的数字波束赋形器。

近年来，混合波束赋形技术因其低成本、低能耗的特点逐渐受到研究者的广泛关注。文献[1]提出基于稀疏空间的S-OMP 算法，核心思想是最小化混合波束赋形矩阵和纯数字波束赋形矩阵之间的欧式距离。但是，S-OMP 算法需要次循环获得模拟波束赋形矩阵FABF，且每次循环都会对FABF进行求逆运算获得数字波束赋形矩阵FDBF[2]。文献[3]通过对HHH进行SVD 分解得到右奇异矢量，将其归一化得到模拟波束赋形矢量FABF，后通过得到的FABF和已知的最优数字波束赋形矩阵得到低维的FDBF。文献[4]提出Beam Steering 算法，是一种结合码本和信道估计的模拟波束赋形算法，但要在天线阵列趋于无穷才能达到最佳性能[2]。文献[5]基于毫米波相控阵架构提出了一种迭代波束成形方法，收发端进行迭代发送和接收信号，找到毫米波信道中具有最大增益的路径，但文献[5]仅仅针对单用户场景并未讨论存在干扰用户场景。

针对以上传统的混合波束赋形方案需要进行信道估计和高维信道矩阵的SVD 分解等问题，本文在毫米波大规模MIMO 系统中设计了一种低复杂度的混合波束赋形方案，通过结合波束扫描和自适应算法避免了信道估计、SVD 分解等问题。由于自适应算法可将主波束对准期望用户和零陷对准干扰用户，因此可以获得良好的信干噪比和频谱效率性能。

1 系统模型

设大规模MIMO 基站（Base Station，BS）端服务于K个用户，BS 处设置M个接收天线。

1.1 阵列模型

智能天线属于阵列天线，由多个相同的全向天线组成。阵列结构可以有多种形式，常见的有均匀直线阵（Uniform Linear Array，ULA）、平面阵以及均匀圆阵（Uniform Circular Array，UCA）等，如图1 所示。

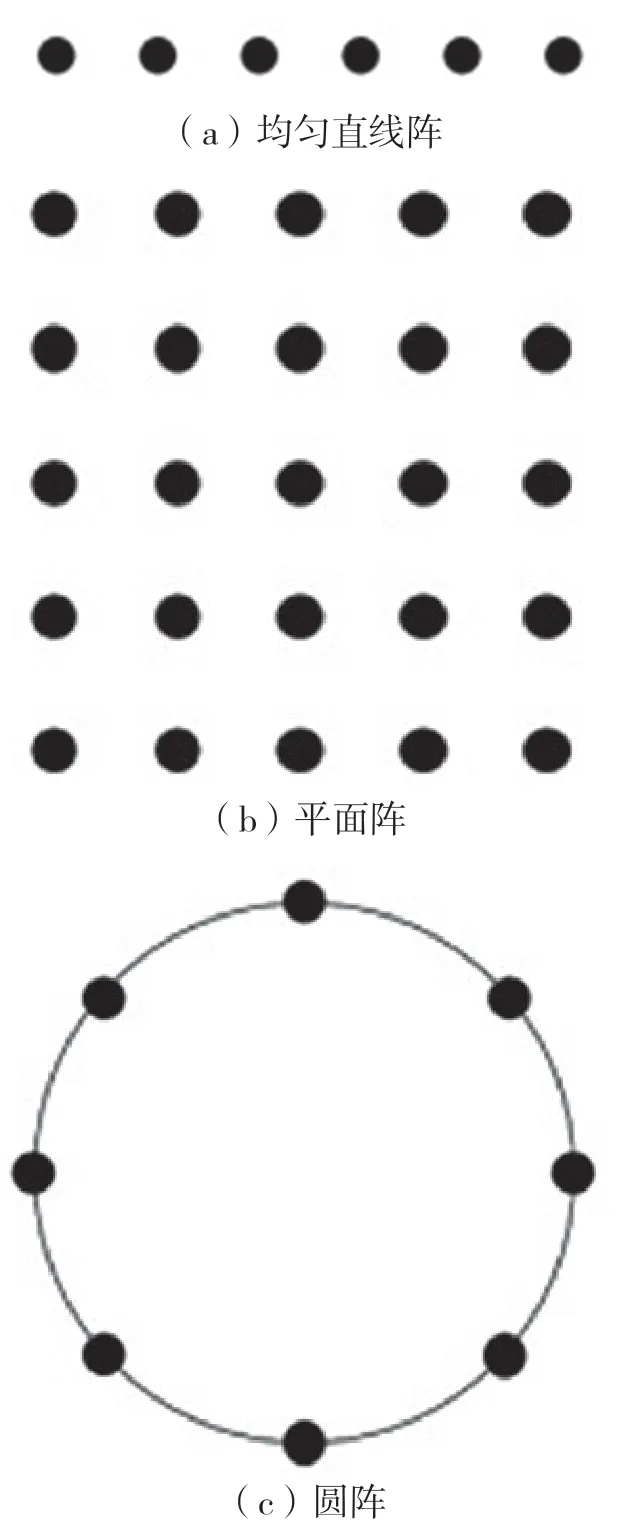
图1 阵列结构

本文采用均匀直线阵，阵列响应表达式如下：

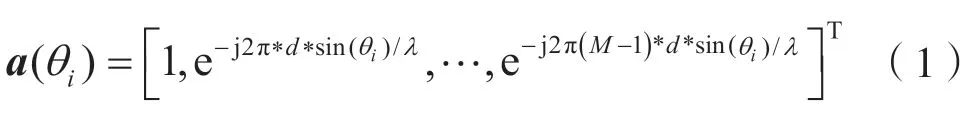
式中，M为天线阵元数量，d为阵元间距，λ为波长，θi(i=1,2,…,K)为方位角。

阵列接收信号模型如下：

式中，x(n)=[x1(n),x2(n),…,xM(n)]T为阵列接收信号矢量；s(n)=[s1(n),s2(n),…,sK(n)]T为信号矢量；θ1为期望用户方向；θ2,θ3,…,θK为干扰用户方向；n(n)=[n1(n),n2(n),…,nM(n)]T，其中ni(n)(i=1,2,…,M) 为第i个阵元上的加性高斯白噪声。

1.2 阵列连接方式

传统的纯数字波束赋形技术需要较多的RF链，将造成系统成本高昂和巨大的能耗等问题。因此，在大规模MIMO 系统中采用混合波束赋形技术成为可行思路。混合波束赋形器按照RF 链与天线的连接方式，可分为全连接型和部分连接型两种结构，如图2 所示。

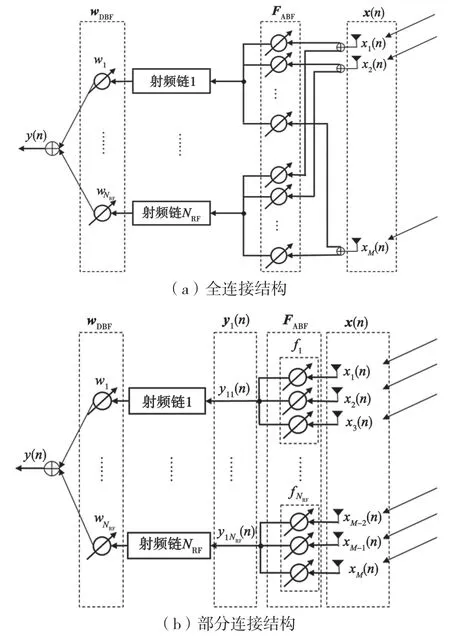
图2 连接模式

在全连接型结构中，RF 链通过移相器与全部阵元连接，可以有效利用大规模天线阵列的阵列增益。但是，这种连接方式十分复杂，需用到MNRF个移相器，导致系统的能耗增加。在部分连接型结构中，天线阵列被分成若干个子阵列。一条RF 链通过移相器仅与一个子阵列中的所有阵元相连接，连接方式简单，使得系统所需的移相器大大减少，有效降低了系统能耗。

由于部分连接型结构连接简单且能耗低，因此具有较强的实际应用价值。本文将重点研究部分连接型结构。完成阵列结构的选择后，阵列的输出表达式如下：

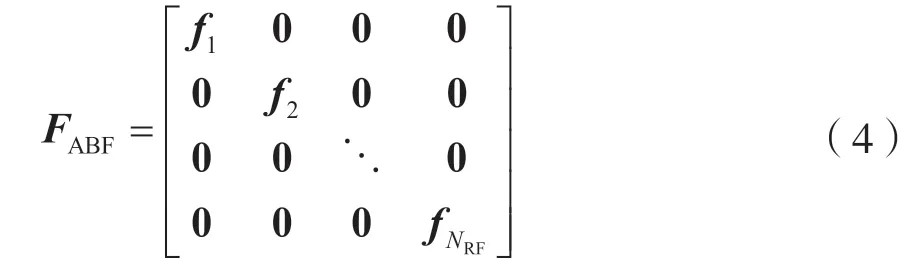
式中，NRF为射频链数量，fi∈，i=1:NRF，Msub=M/NRF为子阵数量。

2 提出方案

本文设计了一种结合波束扫描和自适应算法的低复杂度混合波束赋形方案，方案分为两个阶段，其中自适应算法选择LMS 算法进行分析。

2.1 基于期望信号的波束扫描

在S-OMP 算法中，虽然涉及到码本的设计，但波束是根据与最优数字波束赋形矩阵的残差来选择的。码本设计采用DFT 码本[6]，得到码本波束矩阵为：

式中，N为波束数。

本文为避免S-OMP 算法中的模拟波束赋形涉及信道估计的问题，结合文献[5]只采用一条射频链的思路，提出了一种波束扫描方法，即阵列接收信号通过一条射频链输出到数字域进行迭代搜索，搜索出使得输出信号与期望用户信号的幅度差值最小所对应的波束作为模拟波束赋形矩阵。

本方案具体流程如下。

（1）初始化：误差功率E1=0；快拍数L=512

（2）开始迭代搜索：

（3）找出I1×L中出现次数最多的数值imax

（4）最优波束权矢量为fABF=WABF(:,imax)

由于本文采用部分连接型架构，则式（4）中的矢量fi,i=1:NRF表示如下：

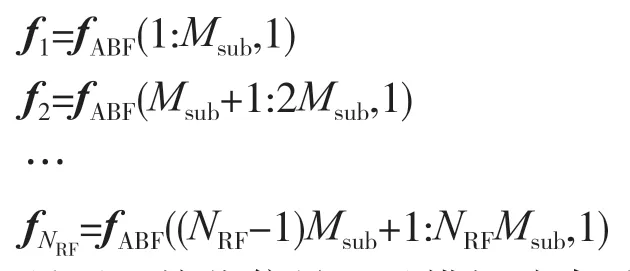
最后，接收信号通过模拟波束赋形后得到的第一级输出：

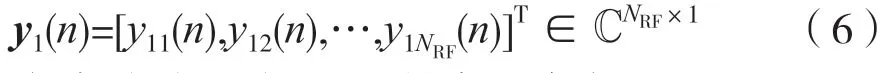
由式（5）可得y1(n)的表达式为：

2.2 LMS 自适应算法

通过2.1 节提出的波束扫描方法，可以得到码本中最接近期望用户方向的波束。本文结合数字域的自适应算法进一步优化波束，可以使主波束对准期望用户方向，同时将零陷对准干扰用户方向，且自适应算法仍然不涉及信道估计、高维矩阵求逆等操作。

本文采用LMS 自适应算法[7]，通过第一级输出y1(n)和期望用户信号s1(n)获得低维的数字波束赋形矢量wDBF，算法如下。

（1）初始化：wDBF=0；L=512

（2）进行迭代：

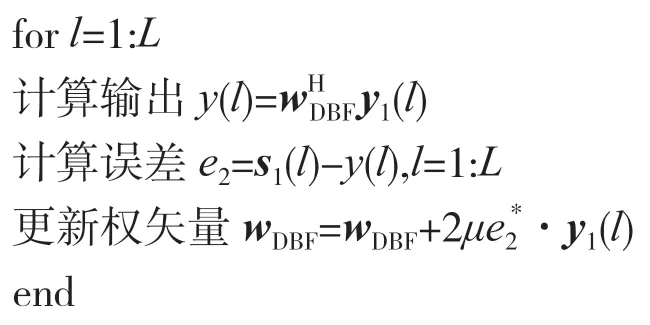
（3）得到最优权矢量wDBF

2.3 信干噪比和频谱效率

本文方案主要通过信干噪比（Signal to Interference plus Noise Ratio，SINR）和频谱效率（Spectral Efficiency，SE）等性能进行评价。混合波束赋形后，输出信号中期望用户功率为：

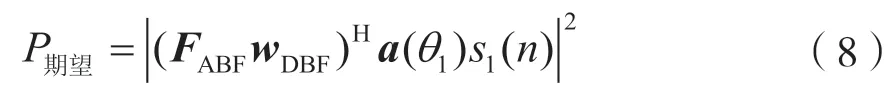
输出信号中干扰用户功率为：

输出信号中噪声功率为：

由式（8）～式（10）可以得到信干噪比：

根据信干噪比，可以得到频谱效率表达式为：

3 仿真结果分析

为了验证所设计混合波束赋形方案的性能，本文分别从信干噪比、频谱效率以及误码率等性能对其进行仿真分析，同时与仅采用波束扫描和纯数字波束赋形进行比较，仿真条件如表1 所示。

表1 仿真条件

实验采用蒙特卡罗的仿真方法，曲线中每一个值都是1000 次仿真的平均值。

3.1 码本设计仿真

本文采用DFT 码本，波束数量设置为4，根据式（5）设计码本波束，仿真结果如图3 所示。

3.2 波束扫描仿真

在得到设计的码本后，通过本文设计的波束扫描方案得到最接近期望用户方向的码本波束，如图4 所示。

3.3 误差收敛分析

实验中，令步长μ=0.0001。第一级输出作为LMS 自适应算法的输入，算法执行完成后可以通过图5 观察算法执行过程中误差的收敛情况。图5 表明，随着信噪比（Signal to Noise Ratio，SNR）的增大，误差收敛加快；在SNR=20 dB 时，迭代50 次即可达到收敛。

图3 码本波束仿真结果

图4 模拟波束赋形波束

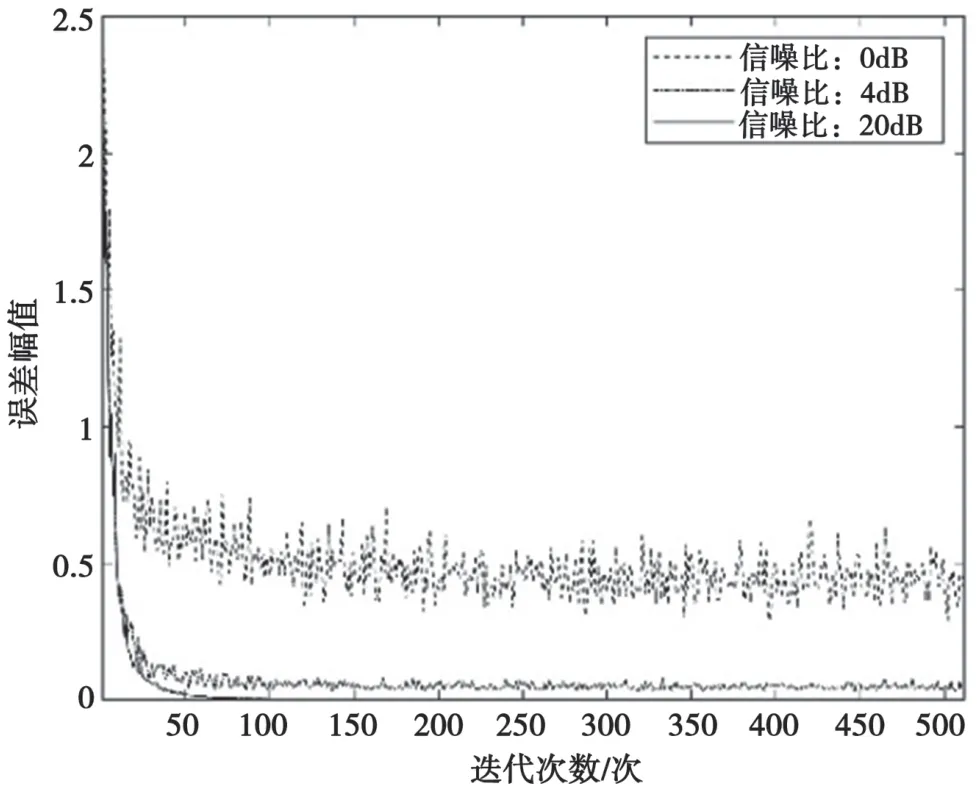
图5 误差收敛情况

3.4 波束方向分析

根据波束扫描得到的FABF和自适应算法得到的wDBF，可以得到混合波束赋形方案的波束图，如图6 所示。图6 表明，自适应算法可以将主波束对准期望用户方向，且在干扰方向形成了零陷，极大地抑制了干扰信号。

图6 混合波束赋形波束

3.5 信干噪比和频谱效率

信干噪比和频谱效率分别如图7 和图8 所示。可以看出，信干噪比和频谱效率随着信噪比的增大而增大；所提出的混合波束赋形方案的信干噪比和频谱效率性能远远高于纯模拟波束赋形的性能，同时接近于纯数字波束赋形的性能。

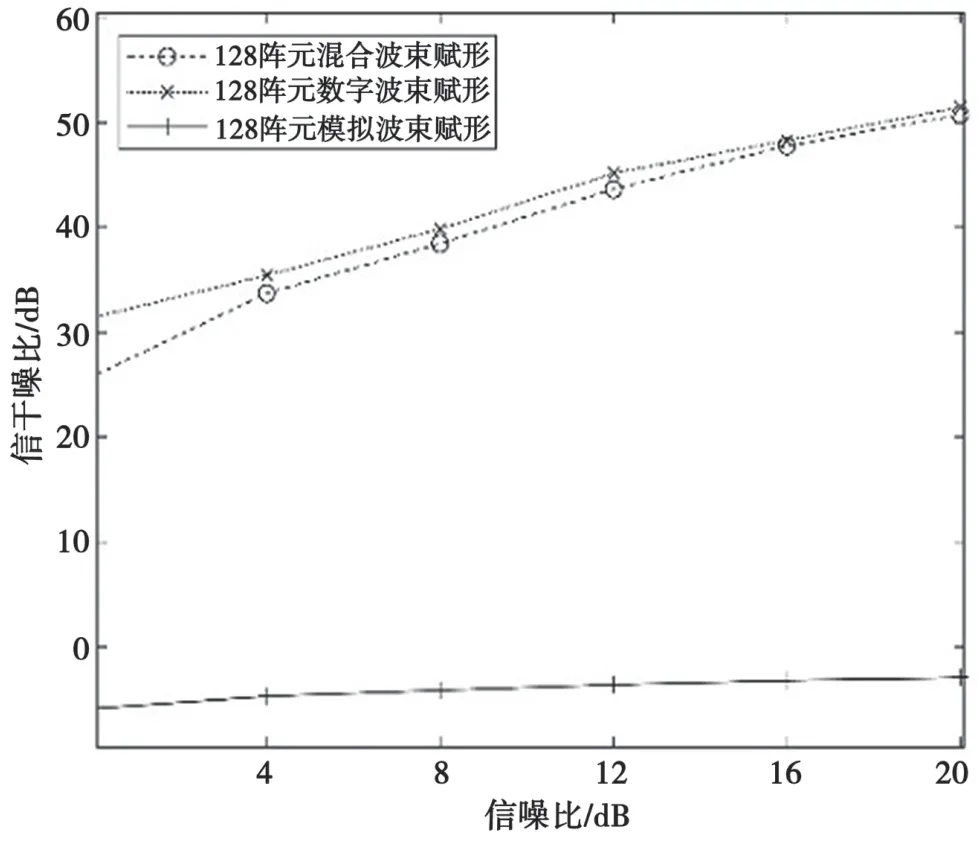
图7 信干噪比仿真结果

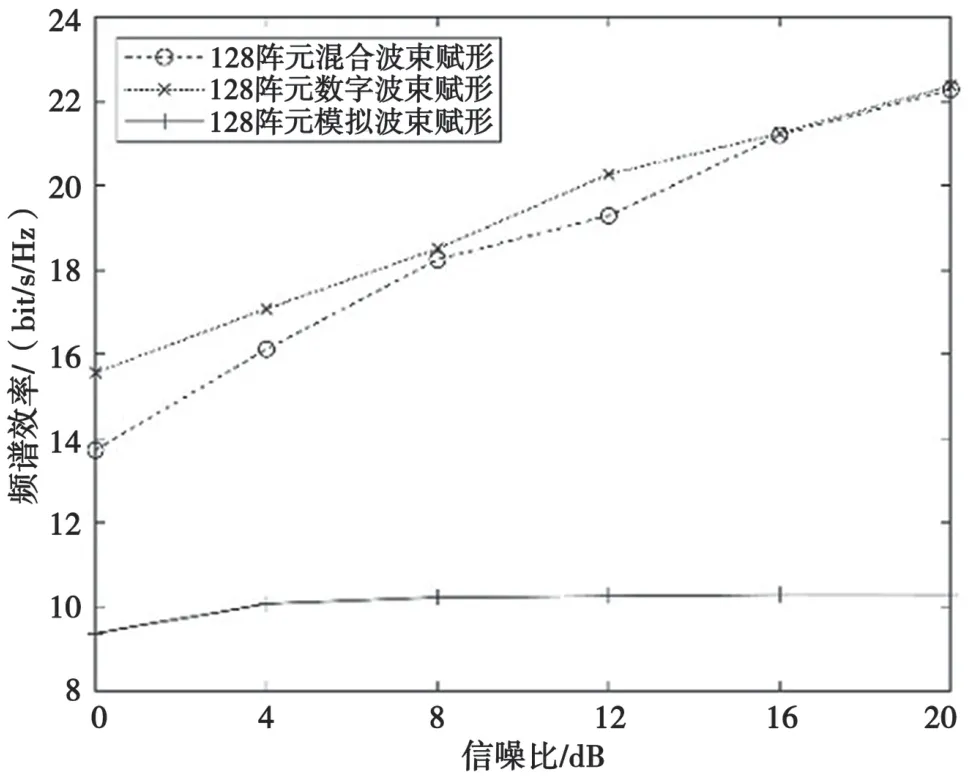
图8 频谱效率仿真结果

4 结论

相较于传统混合波束赋形技术需要进行高维信道估计和SVD 分解等高复杂度操作，本文将波束扫描和自适应算法结合，避免了信道估计和SVD 分解等高复杂度操作。第一阶段的模拟域波束扫描得到与期望用户方向最接近的波束；第二阶段的自适应算法对第一阶段得到的波束进行微调。仿真结果表明，当RF 链数仅为16 条时，混合波束赋形得到的波束图能精确指向期望用户，并在干扰用户方向上产生较深的“零陷”；在信干噪比、频谱效率等性能，所提出的混合波束赋形方案可以很好地逼近纯数字波束赋形。