基于二重加权的作战数据质量评估方法

邱少明，夏长兴，杜秀丽

（大连大学通信与网络重点实验室，辽宁 大连 116000）

0 引言

作战数据质量评估是作战仿真推演中的重要环节之一。当今，随着信息化时代的到来，数据数量呈现指数型的增长，数据质量难以得到保障，对数据质量的评估也更加重要。作战数据质量的评估对改良作战方案、优化指挥决策起到了至关重要的作用［1］。因此，进行作战数据质量评估方面的研究是一项十分重要且迫切的工作。

在作战数据质量评估研究中，众多科研人员已取得了重要性的进展。其中，刘立军［2］构建了六元组评估模型，采用粗糙集［3］与BP 神经网络理论相结合的方法对作战数据进行了质量评估。该评估方法误差小，准确率较高。但BP 神经网络模型的训练需要大量的数据训练集，才能取得较好的结果。当训练集不足的时候，此方法并不能保证评估模型是否实用。杨槐、宫研生等［4］人构建了三层作战数据质量指标体系评估模型，采用统计法与秩心法相结合对作战数据进行了质量评估。该方法接近实际，虽不需要较大的训练集，但方法中专家评判小组的主观偏好对结果影响太大，会出现不同的专家小组得出的结果相差较大的情况。韩志军等［5］人构建了大型仿真推演数据质量的评价指标体系评估模型，采用主观赋权与客观赋权相结合的方法对作战数据进行了质量评估。该方法避免了专家主观偏好对结果影响太大的问题，但该方法中指标值并没有与阈值进行比较，得出的结果也过度依赖指标值的大小，其结果并不能直观地展现数据质量的好坏。结合相关项目与参考相关文献，在作战数据质量指标评估模型的基础上，对作战数据质量评估方法展开了研究，提出了一种基于FAHP 与比较值函数相结合的作战数据质量评估方法，对作战数据质量进行了评估。

1 建立作战数据质量指标体系

作战数据质量指标体系不仅要指出哪些指标是影响作战数据质量的因素，还应该指出指标之间相互的关联关系。影响作战数据质量的因素有很多，但并不需要全部考虑。参考文献［2，4-5］采用层次分解法，将作战数据质量分为固有属性、应用属性和表达属性3 个方面进行评估。固有属性、应用属性和表达属性作为一级分指标来构建数据质量指标体系。其中，固有属性包括客观性、可信性和精确性3 个二级子指标组成；应用属性包括相关性、及时性和全面性3 个二级子指标组成；表达属性包括可理解性、表达一致性和表达简洁性3 个二级子指标组成。在明确作战数据质量指标以及指标间的关联关系后，通过定性指标的定量化，每个指标都可以用一个数量值来表示它的大小，这个数量值称为指标值。作战数据质量指标体系结构图如图1 所示。

图1 数据质量指标体系

在实际项目运行中，邀请多位相关专家，结合文献［2］中相关指标阈值，并依据专家多年经验和项目中数据质量应达到的阈水准来确定指标阈值。每一个指标都有一个阈值，阈值的作用是判断指标值是否达到最低标准。各指标阈值如表1 所示。

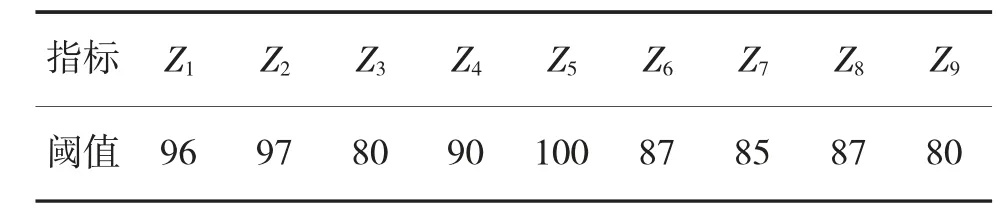
表1 指标阈值表

Zi代表指标，Z1是客观性，Z2是可信性，Z3是精确性，Z4是相关性，Z5是及时性，Z6是全面性，Z7是可理解性，Z8是表达一致性，Z9是表达简约性。

2 二重加权作战数据质量评估方法

专家将对数据质量指标体系中各个指标进行打分，成为指标值。指标值经过作战数据质量评估方法进行计算后，可用一个数量值表示作战数据质量的大小。将作战数据质量评估结果称为结果值，结果值的计算所用如式（1）所示。

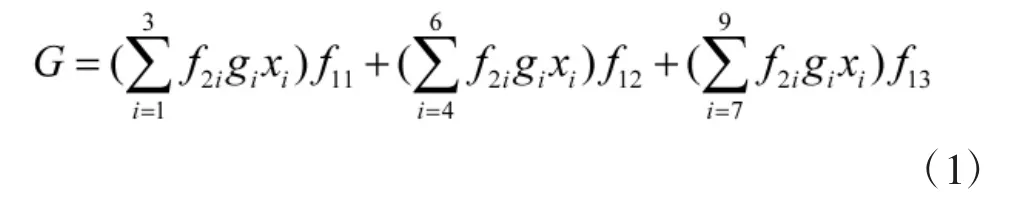
其中，xi为各个指标的指标值，x1、x2、x3、x4、x5、x6、x7、x8、x9分别为Z1、Z2、Z3、Z4、Z5、Z6、Z7、Z8、Z9的指标值。f2i为二级子指标Zi对应的第1 权重，gi为二级子指标Zi对应的第2 权重，f11，f12，f13分别为一级分指标固有属性、应用属性和表达属性所对应的权重。

由公式所知，二级子指标Zi的权重因子主要有两个:1）第1 权重f2i，表示各个二级子指标对作战数据质量的影响，每一个指标对作战数据质量的影响是不一样的，故各个指标的第1 权重也是不相同的；2）第2 权重gi，第2 权重表示指标值和阈值的比较结果，当指标值小于阈值时，表示此指标值低于最低标准，对应第2 权重会降低，指标值大于阈值时，表示指标值大于最低标准，第2 权重增加。一级分指标的权重因子只有一个，表示一级分指标对作战数据质量的影响。

二级子指标第1 权重和一级分指标权重的求解方法，借鉴模糊层次分析法中的求权思想，将指标进行两两比较，求得二级子指标的第1 权重和一级分指标权重。二级子指标第2 权重求解方法，通过构造比较值函数求得第2 权重gi。

2.1 模糊层次分析法

模糊层次分析法（Fuzzy Analytic Hierarchy Process，简称FAHP）是层次分析法结合模糊数学的研究成果［6］，充分考虑到了主观判断的模糊性，是求指标权重最常用的方法之一。模糊层次分析法求指标权重的案例有许多，如文献［7］中对雷达导引头干扰效能指标求指标权重；文献［8］中对射击有力度分析指标求指标权重；文献［9］中对地质灾害危险性评价指标求指标权重等等。通过阅读相关文献，借鉴模糊层次法中求权思想，来求得二级子指标第1 权重和一级分指标权重。

2.1.1 模糊互补判断矩阵的建立

rij表示指标ai和指标aj相对于指标C 进行比较时，指标ai和指标aj具有模糊关系“…比…重要得多”的隶属度。其关于某准则的相对重要程度的描述，可以采用表2 给予的数量标度。

表2 0.1～0.9 标度法及其意义

2.1.2 模糊互补判断矩阵的权重公式

通过指标间的两两比较求得模糊互补判断矩阵后，利用式（2）可以求出各指标的权重。各个指标求指标权重公式［11-12］如下所示:

2.2 构建比较值函数

比较值函数是关于阈值与指标值的函数。阈值与指标值相比较的结果称作比较值，比较值由比较值函数求出。比较值函数的构建需要符合以下3 条标准:1）当指标值小于阈值时，指标值与阈值相距越大，比较值越小，越接近0；指标值与阈值相距越小，比较值越大，越接近1；2）当指标值等于阈值时，比较值等于1；3）当指标值大于阈值时，比较值大于1。比较值与阈值相距越大，比较值越大；指标值与指标值相距越小，比较值越接近1。

根据以上3 条标准，结合函数和分段函数相关性质，构建比较值函数gi公式如式（3）所示:

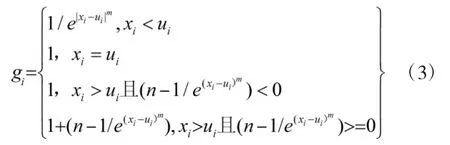
其中，xi是第i 个指标的指标值；ui是第i 个指标的阈值；m，n 为参数，m 用于调节比较值函数的增长速度，n 决定比较值大于阈值时gi的最大取值。通过调节m，n 的大小可以调节gi的大小，让结果更接近标准值。

3 测试结果分析

3.1 测试数据

项目中给出10 组数据，相关专家对这10 组数据中的各个指标进行打分，并对多组数据进行评估，得出评估结果。其中数据中各个指标打分结果及评估结果如下页表3 所示。

3.2 仿真结果分析

由模糊层次分析法思想，将指标间的两两比较，求得模糊互补判断矩阵，利用权重式（2）所得，一级分指标权重和二级子指标第1 权重如表4所示。

二级子指标的第2 权重由比较值函数得出，参考式（3），结合表1 与表3 中的阈值和指标值，当参数m，n 取不同值时，数据集各指标的比较值不同。实验选取3 组数据，分别求得各个二级子指标的比较值，并参考式（1）求得作战数据质量评估结果。具体各个二级子指标比较值和结果值如表5 ～表7所示。

表3 指标打分结果及评估结果

表4 数据质量指标体系权重表

结合表5 ～表7。将仿真结果值与标准值作出对比，对比结果如图2 所示。

作战数据质量评估是作战仿真推演过程中必不可少的一个过程，其评估方法研究也是一个非常复杂的过程。结合相关项目与参考文献，首先用层次分解法，构建了作战数据质量指标体系。其次提出了作战数据质量评估公式，公式中表明有两个权重会影响指标值。之后采用了模糊层次分析法与比较值函数相结合的方法对各项指标确定了第1 权重和第2 权重。由表5 ～表7 和图2 可以看出，当比较值函数两个参数m，n 取不同值时，得出的每个指标比较值也有所不同，仿真结果值都与标准值有一定的误差。但通过3 组仿真结果对比可以得出结论，不断调节比较值两个参数，可令仿真结果值不断地接近标准值，误差会不断地缩小，仿真结果更加接近标准值。

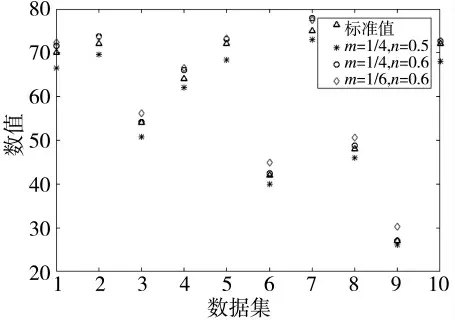
图2 仿真结果值、标准值对比仿真图

4 结论

本文从评估作战数据质量的角度出发，分析了目前存在的几种作战数据质量评估方法的优缺点，提出了基于二重加权理论的方法来对作战数据质量进行评估，在一定程度上克服了现有作战数据质量评估方法的缺点。实验结果表明，所提出的方法简单实用，且仿真结果与标准值相差较小。这在作战仿真推演中具有很高的实用价值，可以提高作战仿真推演结果的正确性，未来具有很高的应用前景。

表5 m=1/4，n=0.5 时比较值、结果值表

表6 m=1/4，n=0.6 时比较值、结果值表

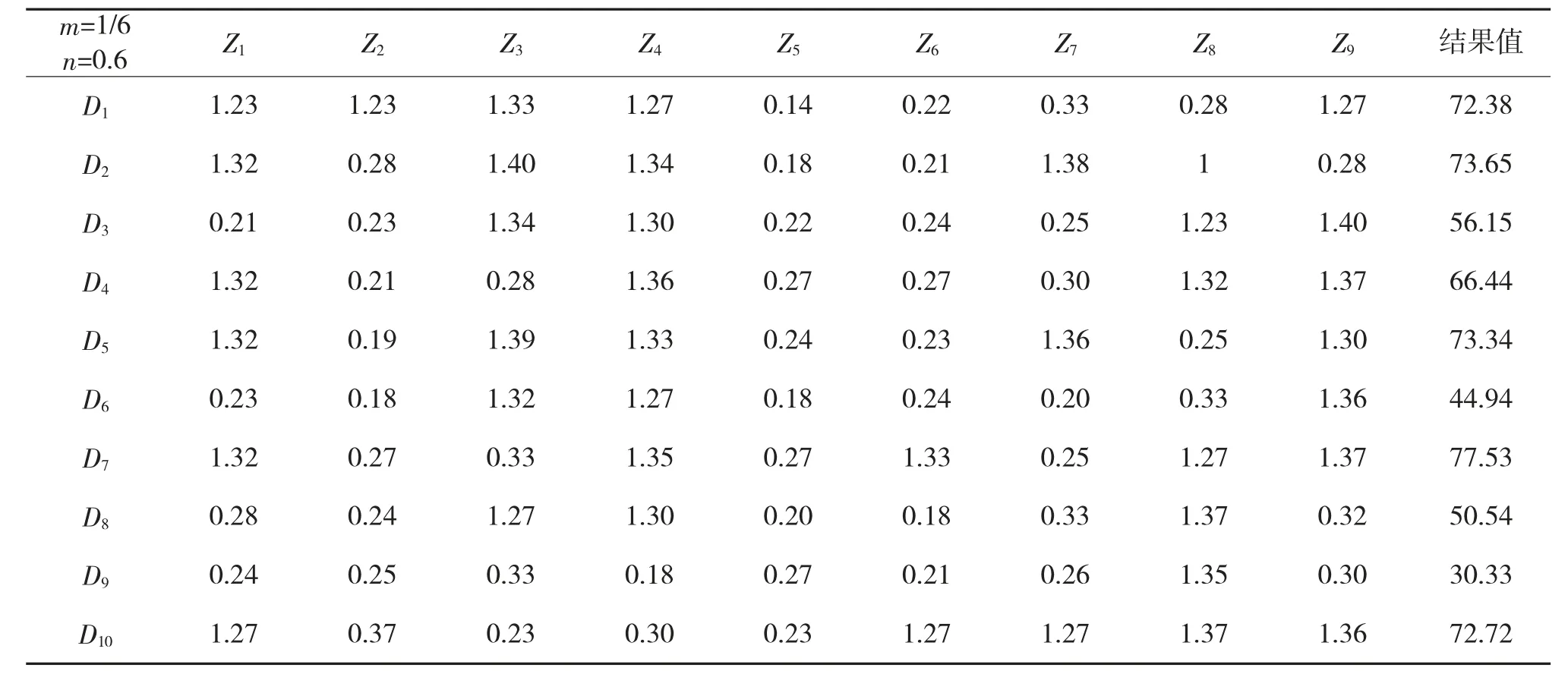
表7 m=1/6，n=0.6 时比较值、结果值表