一种具有解析形式的极化SAR图像CFAR检测新方法*

（中国人民解放军91977部队 北京 100036）

1 引言

20世纪八九十年代，极化SAR图像的目标检测问题引起了广泛的关注，其中以美国林肯实验室Novak等为代表的学者开展了一系列卓有成效的工作［1，3］。1989 年，Novak 对典型场景下静止目标的极化数据进行检测［2］并推导出最优极化检测器和极化匹配滤波器两种检测算法，并给出了在不同参数下的检测概率及虚警概率。1990年，Novak等专家提出了不同杂波背景下的极化白化滤波（PWF）［11］算法，将极化白化滤波检测器、单通道检测器和张量检测器和的检测性能和OPD检测器进行了比较。1990年底，Chaney等比较了OPD、PWF等六种不同的检测器性能［4］。1993年，Novak等利用极化SAR实际数据进行实验，分别采用了非自适应PWF和自适应PWF算法得到滤波图像，并用双参恒虚警率（2P—CFAR）算法来检测目标［5，12］。上述研究主要是基于高斯模型假设下进行，在实际陆地、海洋杂波的模型中SAR图像的背景是空域不均匀的，往往服从非高斯分布。在极化SAR中，非高斯统计模型往往采用多变量乘积模型［13～14］。本文基于纹理变量服从Gamma分布，并采用恒虚警检测方法，推导出了该模型阈值T的解析表达式。新方法大幅度提升了检测性能，在斑点抑制效果和运算量上优于PWF算法，这对极化SAR图像目标检测等应用具有重要意义。

2 多视极化白化滤波检测器建模

POL-SAR的极化散射矩阵有四个分量。一般地，对互易介质而言两个交叉极化分量是相等的。散射矩阵中三个独立的复元素组成目标的极化测量向量x：

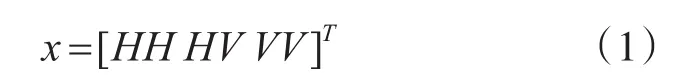
式中，HV是指用水平极化天线接收的目标对垂直极化入射波的散射信号，上标T代表转置。一般情况，假设交叉极化分量HH和同相极化分量HV、VV之间无耦合，而同相极化分量之间存在耦合，此时其协方差矩阵Σ具有如下形式［1］：

变量乘积模型是由纹理变量t，以及复高斯矢量x组成，它们是相互独立的，即［6］

在无场景表面后向散射系数的纹理调制时，式（3）化简为K=x，则x同K服从复高斯矢量分布［7］：

这里，上标H表示共轭转置，d=3是极化特征矢量的维数，|Σ|表示协方差矩阵Σ的行列式。式（2）表明：每个极化通道的观测量被认为是零均值的，即E(x)=0。

对于多视极化SAR数据，其多视协方差矩阵定义为［8］

其中L为视数。对一个均匀场景，多视协方差矩阵X被认为服从多元复Wishart分布，其PDF为［8］

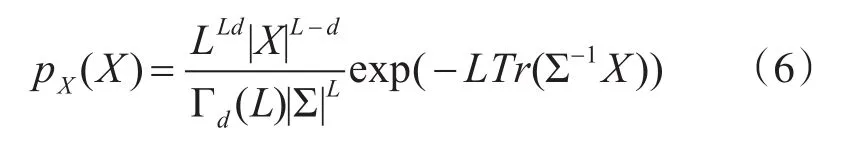
式中，函数 Γd(L)为式（7）所示，Tr(·)表示求矩的迹，Γ(·)表示Gamma函数。

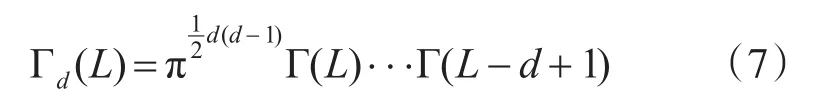
对于多视情况，利用目标多视数据Y及假设正定Hermite矩阵A，构造多视极化白化滤波图像如下［8］：

根据Novak等提出的双参数CFAR检测器，假设SAR数据服从对数正态分布的情况，则强度数据［1］

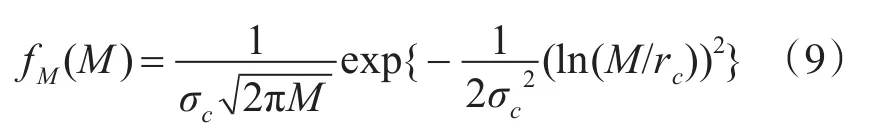
其中，M是像素的强度值，rc与σc分别为M的尺度参数与形状参数。进一步，令ξ=lnu，则随机变量ξ服从式（10）所示的高斯分布［10］：

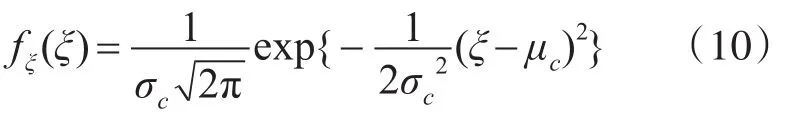
其中，μc=lnrc，σc为u的形状参数。对以上两式可以看出：参数μc与σc分别对应取对数分布后变量的均值与方差。假设T为目标检测阈值T，在虚警概率一定条件下，可得

由此得出随机变量ξ在虚警率pfa下检测阈值T的表达式为

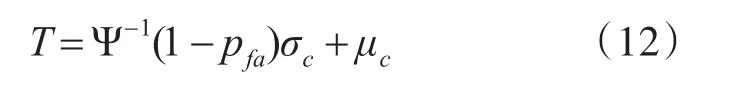
由式（12）可知：ξ与阈值T大小的关系可由下式所示的双参数CFAR检测器表示，即

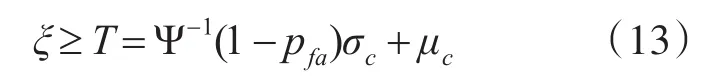
由式（2）可以看出，双参数检测器的检测性能主要取决于目标与杂波功率以及背景杂波的标准差。因此，在包含目标的杂波区域，信杂比越大目标检测越高；而在无目标的杂波区域，杂波标准差越小目标检测概率越高。

3 改进型极化白化滤波模型

多视极化白化图像可定义为

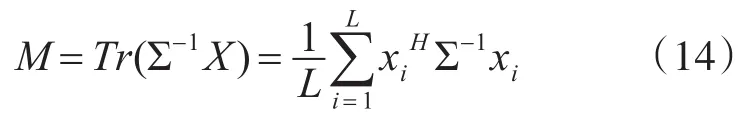
根据多视极化SAR协方差矩阵服从条件复Wishart分布，S N Anfinsen推导出检测量M服从Gamma分布［9～11］：

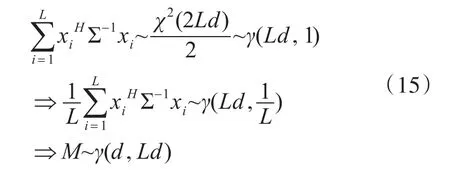
这里γ(μ，β)表示形状参数为a，尺度参数为β的Gamma分布。γ(μ，β)的概率密度函数是

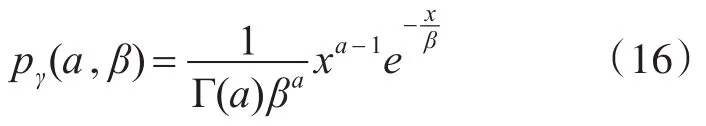
从而推导出M服从的分布表达式为

设检测阈值为T，给定虚警概率，则根据概率论的相关知识可知

则LT=Γ-1[1-pfa，dL] ，上 式 中，所以

其中，Pfa通常选10-4或10-6，L通常为4视。

4 仿真和实测数据检测

图1仿真数据中杂波参数来源于Radarsat-2数据。在Radarsat-2图像中选取舰船目标中一块区域，使用这一区域的协方差矩阵参数作为仿真图像中目标的协方差矩阵参数。杂波仿真同样遵循上述流程，选取海域中不包含目标的杂波区域，以这一区域的协方差矩阵参数作为杂波参数。杂波和目标的协方差关键参数如表1所示。

表1 杂波和目标协方差参数

图1 仿真数据

图1（a）为仿真数据图，使用表1中杂波及舰船目标这两个协方差参数作为仿真数据来源。假设目标及杂波数据服从Wishart分布，利用上述参数采用蒙特卡洛仿真方法对上述两种方法的检测性能进行对比分析。仿真过程中，检测概率pfa设定为10-4。图1（b）和图1（c）中从上至下五个正方形可视为五个舰船目标，对两图可以明显能够看出图（c）存在更多的杂波像素点，在实际情况中这些像素点会极大地干扰对于舰船目标的识别。且改进型MPWF在计算上更加简单，只需要使用视图数及维数这两个参数计算出全局阈值T，就可以对目标图像有一个较好的检测效果。下面分别以表1中杂波1及杂波2为杂波背景，分别使用两种检测方法对仿真图像进行检测，并加入虚警概率pfa为变量，得到的性能对比图如图2所示。

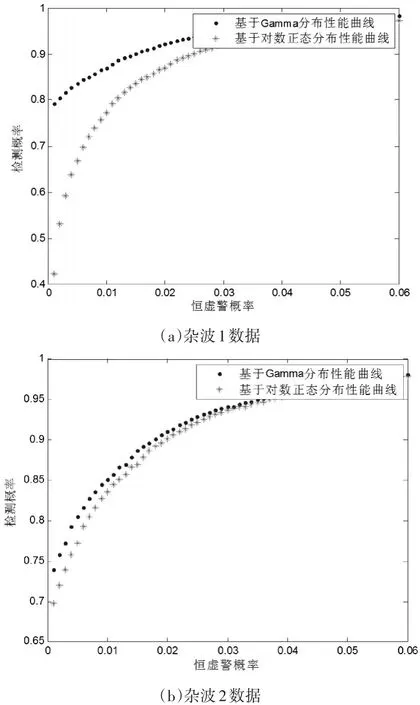
图2 两检测算法检测概率性能对比

从图2（a）和2（b）中可以看出，在两种杂波背景下，都是基于Gamma分布的MPWF算法检测性能更好，其中图2（a）中两检测器性能差距较大，2（b）中量检测器的检测性能十分接近，这是对于不同杂波环境检测器性能变化的正常差异。下面对RADARSAT-2获取的数据进行CFAR目标检测，数据都经过4视处理，经滤波后图像如图3所示。

其中图3（a）为原始图像，图3（b）、（c）为pfa=10-4的两模型检测图像，图 3（d）、（e）为pfa=10-6的检测图像。由图3（a）能够看出，在植被区域MPWF改进模型检测算法对于舰船目标具有较好的检测效果，在大体上和目标的形状、特性相吻合。相比较而言，基于对数正态模型MPWF检测算法并不能很好地体现出明显的滤波效果，只在舰船目标位置又少数亮点出现。

图3 两算法对比结果

对数正态分布检测结果不理想的主要原因在于基于对数正态模型的MPWF检测算法无法满足目标区域检测统计量的精确建模，而改进型模型并不存在此类缺陷。

5 结语

本文针对MPWF算法运算量大的问题，提出了一种改进型极化白化滤波模型。实验结果表明，该模型不仅可以显著地降低了运算量，而且可以有效抑制相干斑，更好地保留了图像的边缘等细节信息，更好地为后续的目标检测工作提供保障。