水工弧形钢闸门自振特性研究

程志新，张港

（华北水利水电大学 机械学院，河南 郑州 450045）

引言

弧形闸门因无门槽、启门力小、操作方便等优点而大量用于各种水道工作[1]。在水利工程运行过程中，弧形闸门受到水流的脉动作用会产生不同程度的振动，这种闸门与水流相互耦合产生的闸门振动称为流激振动，结构会发生变形、磨损以及腐蚀的现象[2]，这些都是引起弧形闸门失事破坏的源头[3]。为避免其遭受破坏，可以从两个方面入手：一是改善闸门进出水流流态，尽量避免异常水流荷载的产生；二是优化其结构，改变自身固有频率来避免水激励力的高能区作用。但是由于改变水流流态一定会引起其它水工结构的改变，实施起来较为困难。因此，首要研究的是弧形闸门结构和动力特性，以便有效减少弧形闸门的失事破坏现象的发生。

1 研究方法

由于弧形闸门是复杂的空间板梁结构，也很难测定作用其上的水流脉动压力，所以在对弧形闸门进行动力分析时，大都是先计算弧形闸门的自振频率，在与作用水流的脉动频率相比较，来使其自振频率远离高能脉动频率区，确保闸门工作环境的安全[4]。

许多实验资料表明现在已经能准确得到水流脉动频率，水流脉动主频率主要在1至20Hz之间浮动，其中有48.3%在1至10Hz之间变化，超过20Hz的很少。闸门结构在水中的振动属于流体弹与性理论研究的内容，闸门的振动是两者协同作用的结果，所以要用弹性结构与流体的耦联振动理论来分析其振动特性。但是闸门振动本身就是一个很复杂的问题，所以目前普遍采用理论分析的方法，计算闸门在空气中的自振频率，再通过水力学试验测定振动扰力，即水流总脉动压力的幅值和频率，以检验闸门是否发生共振[5]。

由于作用于门体的水动力载荷难以采用函数式表示，载荷作用机理尚不完全清晰，并且弧形闸门承受的动水压力是一个连续波动的过程，时均压力上下波动的水流作用力就是脉动压力。因此，在对弧形闸门自振特性进行研究时，采用有限元模态计算与原型观测试验相结合的方法，即简化边界条件，设定理论分析的工况参数，在有限元模态计算的基础上，通过原型观测试验，对理论计算分析和设计计算的成果进行验证。

2 工程实例

2.1 工程概况

本文以陕西汉江蜀河水电站泄洪闸弧形工作闸门为研究对象，孔口尺寸13.0×24.3m（宽×高），弧形闸门半径32m，底槛高程193.5m，支铰高程217.6m，设计水头23.8m。整体采用的是三支臂结构、球铰支承，使用悬挂式液压启闭机启闭，启闭机容量为2×4000kN。本文主要对弧形闸门在动水试验水位216.15m下的自振频率和模态进行了计算分析。

2.2 有限元计算

2.2.1 有限元模型

采用AUTODESK公司商业软件Inventor 2011建立弧形闸门有限元模型，对闸门的部分结构进行了一定简化，例如省略了止水部件、侧轮装置、所有螺栓螺母、栏杆等，建立的模型如图 1所示。弧形闸门有限元计算选取四面体单元（Solid187 element）和六面体单元（Solid186 element）混合而成的组合有限元模型，单元的划分基本上按弧形闸门结构布置上的特点采用自然离散的方式，将面板、横梁腹板、横梁翼板、纵梁腹板、纵梁翼板、吊耳、支臂腹板、支臂连接杆等构件划分为六面体单元，支铰、轴承、铰轴划分为四面体单元。

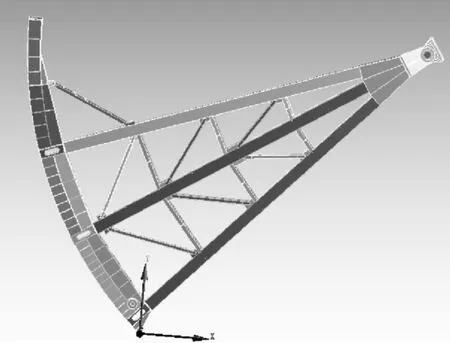
图1 弧形闸门有限元模型

2.2.2 边界条件

（1）水压力载荷

水压力直接作用于面板外壁上，水体密度取 1000kg/m3[5]，面板分布水压力根据水头按下式计算：

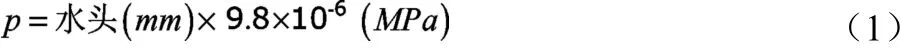
静力挡水工况闸门水头为22.65m，荷载动力系数取1.0。水压力宽度范围为面板宽度 12.9m，高度范围为面板底缘到正常高水位 22.65m，水压力从顶部的 0逐渐增加到底部的221970Pa。

（2）闸门自重

闸门自重方向向下，由三维建模软件自动计算，闸门门叶重 165724kg，支臂重 198623kg，支铰（铰座+铰轴）重53000kg，轴承重 2194kg，（门叶+支臂+铰链+铰轴）为419541kg。

（3）止水摩擦力

考虑侧止水橡皮的摩阻力，侧橡胶止水型号为 L60（SF6674），预压缩 4mm，橡皮头部宽 60mm，与不锈钢摩擦系数为0.5。

3 试验结果与讨论

3.1 有限元计算结果

通过有限元计算得到弧形闸门在动水试验水位下的模态振型和参数，这里取前4阶。其前4阶自振特性分析结果如表1所示，振型图取前3阶图3所示。

表1 闸门结构自振频率 单位：Hz

模态分析结果表明，闸门全闭挡水工况的基频在 4.4Hz左右。由图2可以看出，弧形闸门的第一阶振型以门叶扭曲为主；第二阶振型以支臂部分的弯曲为主，弯曲方向向内，呈靠拢趋势；第三阶振型以支臂和门叶部分同时弯曲为主，弯曲方向为Z向。

图2 弧形闸门振型图

3.2 原型观测试验结果

通过改进随机子空间法得到弧形闸门的自振频率，经计算整理，结果如表2所示。

表2 弧形闸门自振频率

由表2可以看出，主梁的自振频率要大于支臂，其中支臂的自振频率从一阶到四阶增加较为稳定，而主梁的自振频率在第三阶和第四阶之间有较大增加。

3.3 结果对比分析

对弧形闸门自振频率的有限元模态计算结果和模态测试结果进行整理，如表3所示。

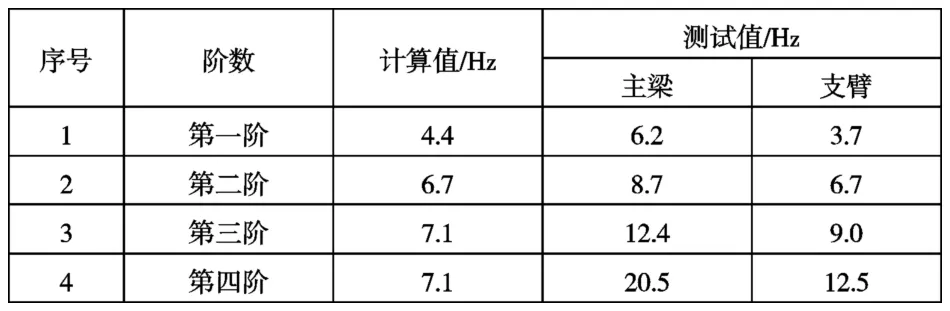
表3 弧形闸门自振频率模态计算结果与测试结果对比表

由表3可以看出，主梁测试所得到的自振频率值最大，闸门经计算得到的自振频率值最小。弧形闸门前三阶，也就是在低阶阶段的自振频率计算值与测试值契合度较高。但是弧形闸门存在制造和装配误差，运行条件无法预判等问题，实际运行工况下的边界条件远远要比理论计算繁琐，使得四阶（含四阶）以上自振频率测试值高于计算值，但都有一致增大趋势[6]。

4 结语

本文对弧形闸门自振特性进行了研究，提出了一种将有限元模态计算与原型观测试验相结合的方法，并以蜀河水电站弧形闸门为例展开算例分析，先通过有限元模态计算得到弧形闸门的自振频率，然后通过原型观测试验中的模态测试进行验证与分析。本文所提出的方法能极大满足水工闸门工程分析的要求，计算结果为弧形闸门振动故障诊断及预报及其结构动力特性的优化设计提供了依据，可供同类型闸门振动稳定性研究借鉴。